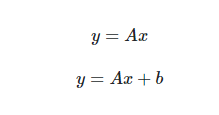
- 참조: https://gaussian37.github.io/vision-concept-homogeneous_coordinate/
- 참조: https://darkpgmr.tistory.com/78
목차
- Homogeneous coordinate의 의미와 사용 이유
- Homogeneous coordinate의 사용 예시
- Homogeneous coordinate 내용 정리
Homogeneous coordinate의 의미
Homogeneous coordinate를 다루기 이전에 Affine Transformation에 대한 개념이 필요하다.
homogeneous 좌표계를 사용하면 affine 변환이나 perspective(projective) 변환을 하나의 단일(single) 행렬로 표현할 수 있기 때문이다.
보통 어떤 벡터를 Transformation을 할 때, Transformation Matrix를 곱해주어서 변환하게 된다. 선형변환 (rotation , shear 등)등의 경우
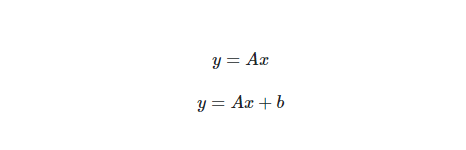
에서 위 식이 가능하다. A = transformation matrix (위 식: 기본 선형변환, 아래 식: affine 변환)
하지만 affine 변환의 경우 Transformation Matrix를 곱해주는 것만으로는 변환이 가능하지 않다. 이동성분 b를 필요로 하기 때문이다.
affine transformation 도 위 식처럼 표현할 수 있을까(단순히 벡터에 transformation matrix를 곱하여 affine transformation을 하는 방법이 있을까)라는 질문에서 도입된 개념이 Homogeneous Coordinate이다.
그러려면 포인트의 transformation과 벡터의 transformation을 한번에 표현하는 transformation matrix를 구해야 한다.
homogeneous coordinate의 핵심 개념
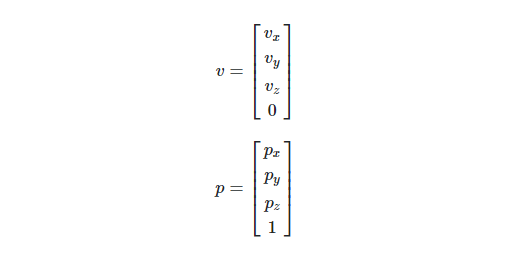
N차원의 벡터와 포인트를 표현할 때, N+1 차원의 벡터와 포인트를 사용한다.
예를 들어 벡터의 경우 식 (5)와 같이 차원을 하나 추가하고 추가된 차원에는 0을 사용한다. 반면 포인트의 경우 식 (6)과 같이 차원을 하나 추가하고 추가된 차원에는 1을 사용한다.
이와 같은 형태로 transformation matrix를 사용하게 되면 벡터와 포인트에 대하여 linear transformation과 translation을 하나의 transformation matrix로 표현할 수 있다.
만약 homogeneous coordinate에서 원래의 좌표를 구하려면 끝 자리가 1이 되도록 scale을 바꾼 후 1을 때어내면 된다. 예를 들어 homogeneous coordinate에서
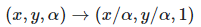
로 바꾼 다음 2차원 실수 좌표계에서는
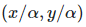
로 표현할 수 있다.
Homogeneous coordinate의 사용이유
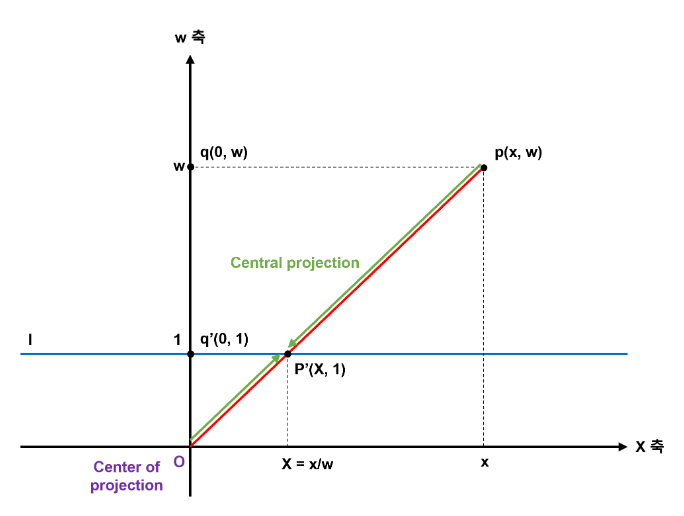
homogeneous coordinate를 다루는 이유는 좌표계가 projection과 관련되어 있기 때문이다.
homogeneous coordinate는 3차원에서 정의된 3차원 가상 공간 객체의 2차원에 투영된 이미지를 얻는 것과 관련되어 있고, homogeneous coordinate를 사용하면, 3차원 공간의 affine 변환들을 모두 4 x 4 행렬로 표현할 수 있다.
-
2차원 공간의 좌표(x,y)는 (x,y,1)로 표현할 수 있고, 이는 보통 행벡터로 생각을 하고 열벡터로 표현할 경우 [x,y]T 또는 [x,y,1]T로 표현할 수 있다.
-
3차원 공간의 좌표를 표현하는 벡터 [x,y,z]T는 Homogeneous coordinate에서 [x,y,z,1]T로 표현할 수 있지만 일반적으로 마지막 숫자를 1이 아닌 다른 값도 가질 수 있도록 W로 표현하기도 한다.