시계열 데이터

시계열 데이터란? 시간의 흐름에 따라 관측치가 변하는 데이터

일반 데이터 vs 시계열 데이터

모델 성능을 살펴보았을 때, 시계열 데이터의 경우 데이터를 섞었을 경우 모델 성능에 변화가 나타남. 반대로 일반 데이터의 경우 데이터가 섞여도 영향을 그리 크게 받지 않음

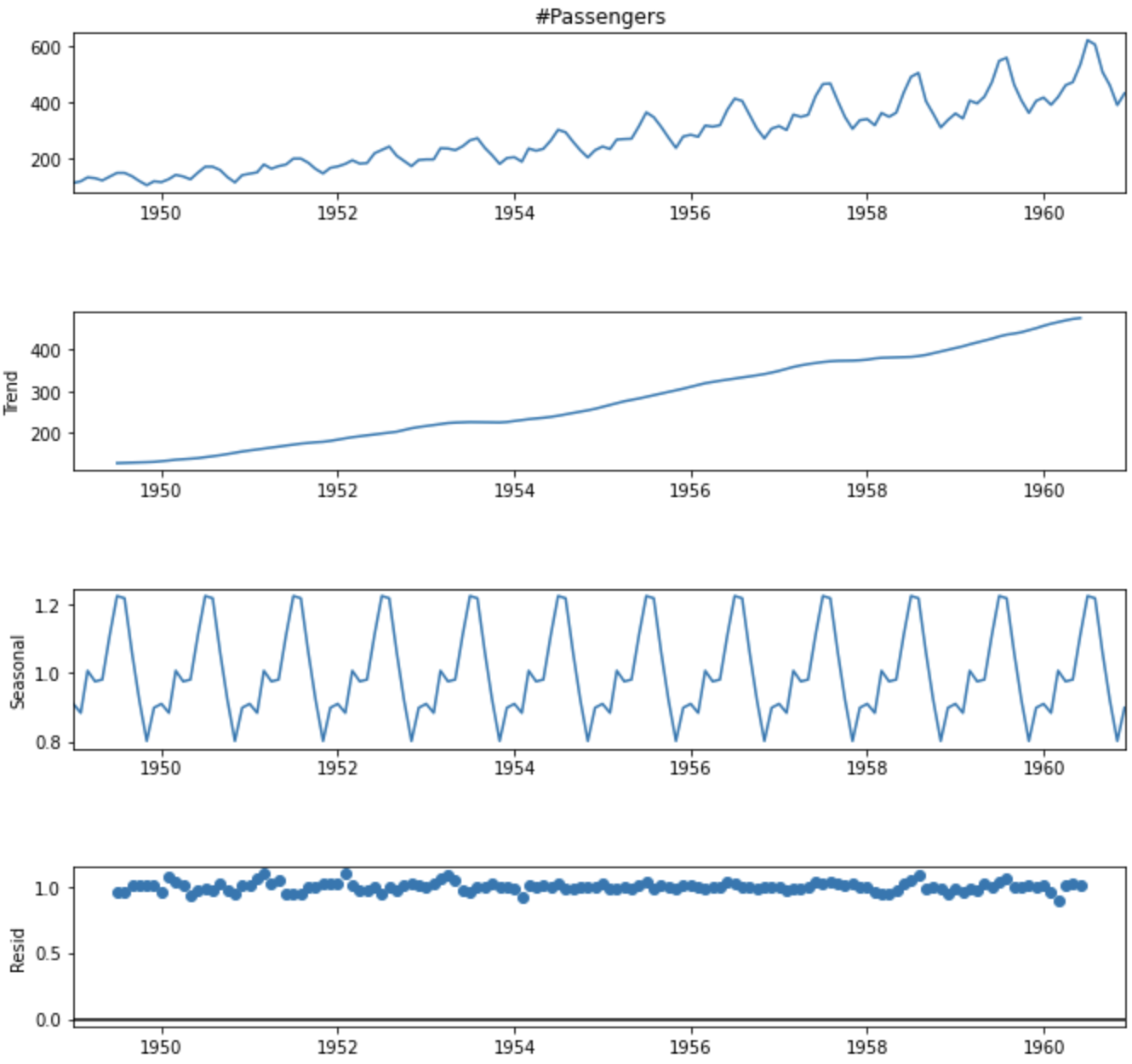
전통적인 시계열 데이터 성분(3)

1. 추세(Trend) : 구간별로 어떻게 변화하고 있는지
2. 계절(Seasonal) : 주기성은 어떻게 나타나는지
3. 불규칙(Irregular / Residual) : 잔차(추세, 계절에 나타나지 않은 경우)

정상 시계열 vs 비정상 시계열

1. 정상시계열 : 평균, 분산이 일정한 범위 내에서 변화한다.
   => 평균, 분산이 'bounded' 되어있다.
2. 비정상시계열 : 평균, 분산이 발산 혹은 수렴하는 것들

정상 VS 비정상 시계열 구분 : 자기상관함수(ACF)

• 자기상관함수 : 특정 데이터와 시차가 적용된 데이터들의 상관관계를 보는 것
• 정상시계열의 자기상관함수 : 추세가 뚜렷하지 않기 때문에 ACF가 빠르게 감소
• 비정상시계열의 자기상관함수 : 추세가 뚜렷하기 때문에 ACF가 천천히 감소

정상 시계열 예측 모델 : ARIMA, SARIMA

• ARIMA : AR(AutoRegressive) + MA(Moving Average)
• 자기회귀모델(AR) : 과거 관측값을 이용해 현재 혹은 미래의 값을 설명하는 모델
• 이동평균(MA) : window를 기준으로 앞, 뒤 값을 표준으로 값을 치환 -> 노이즈 감소
• SARIMA : ARIMA 모델에 계절성 시계열을 추가로 모델링하여 더한 것

import pandas as pd
import statsmodels.api as sm
df = pd.read_csv('file path')
df.head()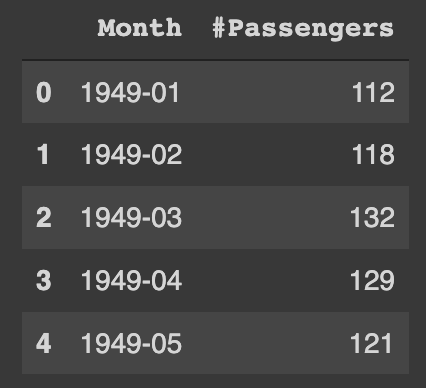

df['Month'] = pd.to_datetime(df['Month'])
df = df.set_index('Month')
df.plot(kind='line')
df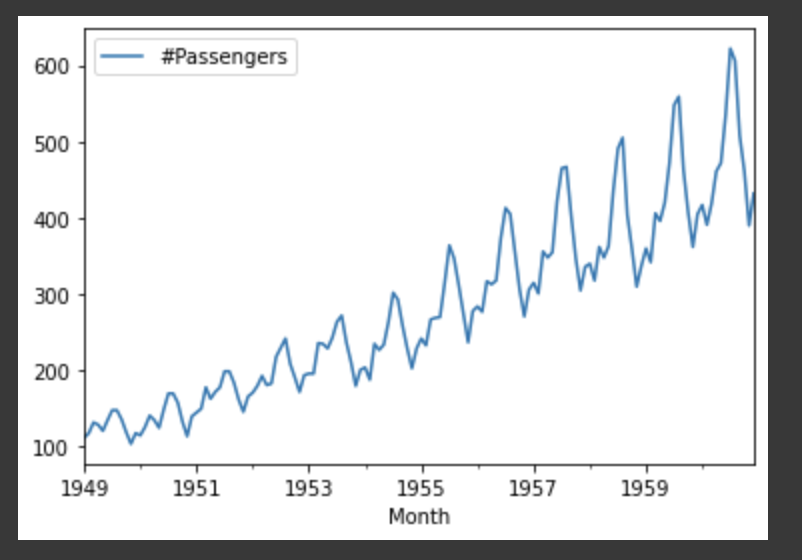

import matplotlib.pyplot as plt

decomposed = sm.tsa.seasonal_decompose(df["#Passengers"], model='additive')
fig = decomposed.plot()
fig.set_size_inches(10, 10)
plt.show()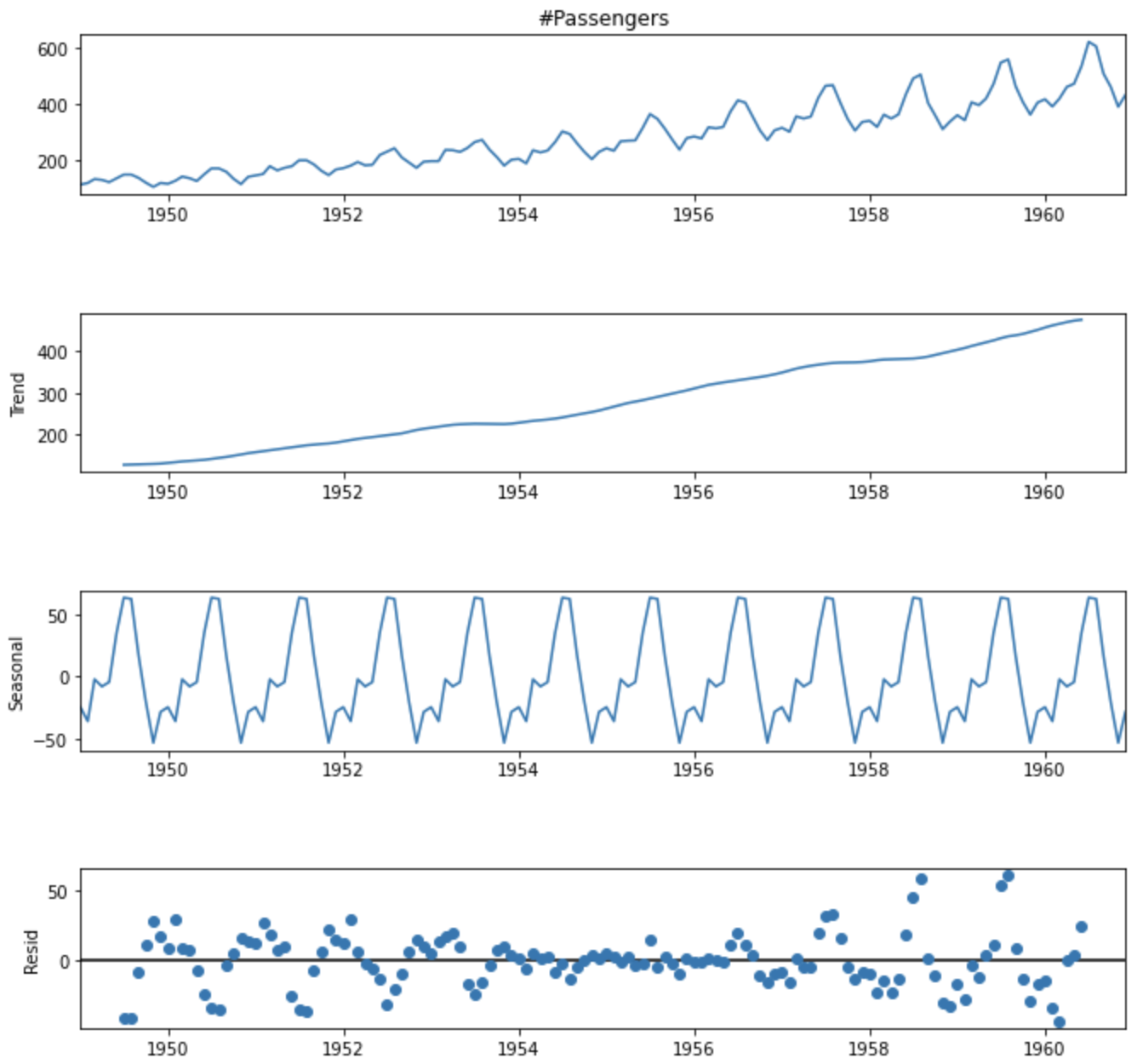

import matplotlib.pyplot as plt

decomposed = sm.tsa.seasonal_decompose(df["#Passengers"], model='multiplicable')
fig = decomposed.plot()
fig.set_size_inches(10, 10)
plt.show()