문제 : 연속부분 수열 합의 개수 (출처 : 프로그래머스)
📌
초반에는 완전탐색 문제인줄 알고 아 쉽네 했는데
삼중 반복문을 만나고 나서 완전 탐색으로는 해결할 수 없음을 깨달았다.
결론은
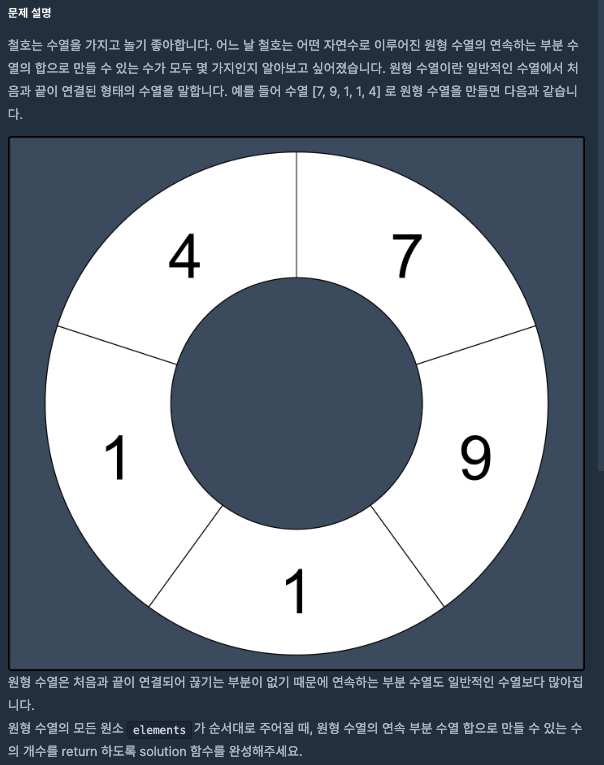
"원형 배열" 과 "부분 합" 의 특성을 활용했어야 했다는 것이다.
이전에는 단순히 특정 구간의 합을 구하기 위해서는 반복문 / sum을 이용해왔었다.
사용한 개념은 간단했다.
원형 배열의 부분합을 구할 것이기 때문에 원래 배열의 길이에 2배를 한 후 충분한 누적합을 구하게 하는 것이다.
이때 누적합은 초기값을 할당함으로 기본 for 반복문보다 더 좋은 시간 복잡도를 갖도록 이끄는 것이다.
- 누적합을 구하기 위한 배열 공간 확보 맟 0 세팅
- 기본 for 반복문보다 유리한 누적합
- 원형 배열의 수 X2를 했기 때문에 부분합이 전부 나오게 됨
🧚
def solution(elements):
answer = 0
elements_x2 = elements * 2
prefix_sum = [0 for _ in range(len(elements_x2))]
print(prefix_sum)
prefix_sum[0] = elements_x2[0]
for i in range(1, len(elements_x2)):
prefix_sum[i] = prefix_sum[i-1] + elements_x2[i]
print(prefix_sum)
nums = set()
for length in range(1, len(elements)+1):
for i in range(len(elements)):
sum = prefix_sum[i+length] - prefix_sum[i]
nums.add(sum)
answer = len(nums)
return answer문제 : n^2 배열 자르기 (출처 : 프로그래머스)
📌
생각보다 시간복잡도때문에 고민을 했던 문제이다.
집중력문제도 있었던 것 같기도 하다.
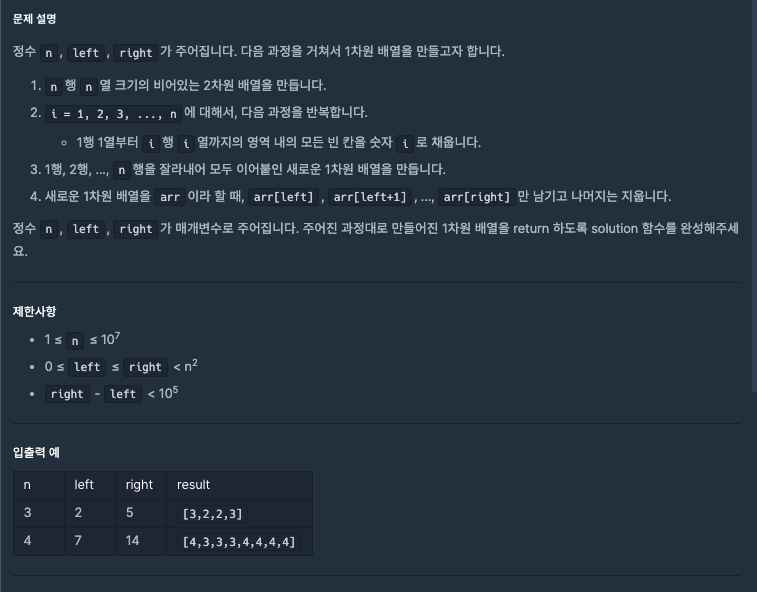
힌트는 제한사항에 있다.
n은 10의 7제곱까지이다. 이는 이중 구조문만 가더라도 상당한 숫자이다.
그 다음줄을 봐보자. right - left의 범위가 나와있다.
이는 n의 범위보다 작은 숫자이고
이를 이용해 한번에 정답 배열인 answer을 완성해야 한다는 말이다.
해당 문제는 기존 문제들과 다르게 문제의 흐름대로 코드를 작성하게 된다면 낭패를 보는 문제였다.
문제를 정의하는 것은 좋았으나 그 안의 간단한 의미를 파악한 후 겉으로 보이는 단순한 규칙을 이용해 풀 수 있다.
간단한 의미란 몫과 나머지를 이용해 행과 열을 구할 수 있다는 것이다.
겉으로 보이는 단순한 규칙은 방금 구한 행과 열의 숫자 가운데 Max 값을 할당한다는 것이다.
max 내장함수의 시간 복잡도는 O(n)이다.
🧚
def solution(n, left, right):
answer = []
for one in range(left, right+1):
answer.append(max(one // n + 1, one % n + 1))
return answer