- 스탠퍼드 대학의 CS231n: Convolutional Neural Networks for Visual Recognition

본 포스팅은 CS231n 2강의 내용을 정리한 것이다. 이곳에 출처가 따로 언급되지 않은 이미지들은 스탠퍼드 대학에서 제공하는 강의 슬라이드에서 가지고 왔다.

[CS231n] http://cs231n.stanford.edu/2017/syllabus.html

Image Classification

이미지 분류는 컴퓨터 비전 분야의 핵심 과제이다. 컴퓨터는 인간과 달리 이미지를 숫자로 본다. 이를 Semantic Gap 이라 한다.

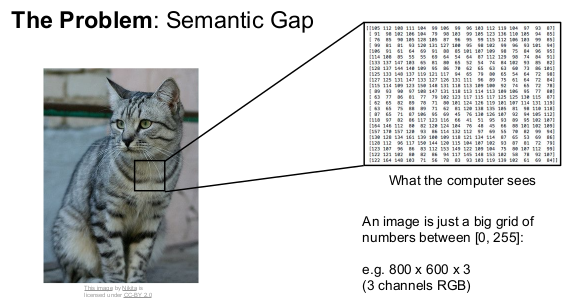
그러나 다음과 같은 상황에서 컴퓨터는 이미지를 제대로 인식/뷴류하지 못한다.

• 관점 변화 (Viewpoint variation) : 카메라가 조금만 움직여도 픽셀값이 변한다.
• 빛 (Illumination) : 빛의 차이
• 자세 변화 (Deformation) : 특이한 자세
• 가려짐 (Occlusion) : 물건의 일부만 보이는 경우
• 배경과 겹쳐질 때 (Background Clutter) : 배경과 분류 대상이 색이 비슷할 때
• 같은 종류의 변주 (Intraclass variation)

이미지 분류기 (An image classifier)

이미지를 분류하기 위해서 '이미지 분류기'를 필요하다. 기존에는 edge와 corner로 이미지를 분류하는 시도가 있었지만, 이 방법에는 일반화할 수 없다는 한계가 있었다.

그래서 Data-Driven Approach(데이터 중심 접근방법) 를 사용했다. Data-Driven Approach는 이미지와 이름표(labels)로 이루어진 데이터를 모아 머신러닝을 사용해 이미지 분류기를 훈련한 후, 새로운 이미지의 이름을 예측하는 방법이다.

1) Nearest Neighbor

첫 번째 분류기 방식인 Nearest Neighbor는 모든 이미지와 그에 해당하는 이름을 수집하고 모두 외운 후, 새로운 이미지가 들어오면 기존에 가지고 있는 이미지와 비교하여 가장 비슷한 이미지를 찾아 새로운 이미지의 이름을 예측한다. 즉 A라는 새로운 이미지를 넣으면 컴퓨터는 'A는 B와 비슷하게 생겼으니 얘의 이름은 B일 거야'라고 예측을 하는 것이다.

예를 들어 설명하기 위해 CIFAR10 이라는 데이터 세트를 가지고 와보자.

• 참고문헌: https://www.cs.toronto.edu/~kriz/cifar.html

CIFAR10은 10개의 클래스로 구성된 5만 개의 Traning images와 1만 개의 Testing images이다. 오른쪽 이미지의 1행은 testing images이고 나머지 10개의 행은 NN 분류기를 통해 컴퓨터가 인식한 결과이다. testing images와 거리가 가까운 순서대로 먼저 인식하게 된다. 4열의 개구리를 보면 컴퓨터는 개구리를 제일 먼저 고양이(1번째 그림)으로 인식하고 9번째로 비행기(9번째 그림)로도 인식하고 있음을 알 수 있다.

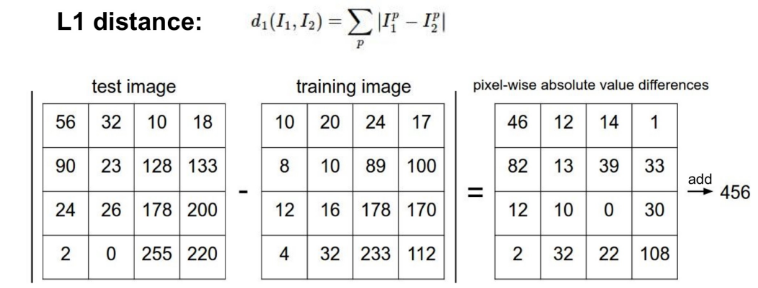
이미지들을 비교하기 위해 NN 분류기는 L1 Distance 를 사용한다. L1 Distance는 숫자로 표현한 테스트 이미지와 트레이닝 이미지를 뺀 값에 절댓값을 붙여 합한 결과이다.

NN 분류기의 학습과 예측의 시간은 얼마나 걸릴까? (시간복잡도)

데이터가 N개가 있으면 NN 분류기의 학습 시간은 1이 걸리고 예측 시간은 N이 걸린다. NN 분류기는 주어진 정보를 그대로 가지고 있어서 학습 시간은 짧다. 그러나 예측을 할 때는 N개의 이미지를 일일이 비교해야 하므로 N의 시간이 걸린다.

그러나 우리는 학습 시간이 길어도 예측 시간이 짧기를 원하므로(비효율적) 이 방식은 좋지 않다.

2) K-Nearest Neighbors

• 출처: https://commons.wikimedia.org/wiki/File:KnnClassification.svg

위의 그림에서 초록색 원을 어떤 것으로 분류해야 할까?

첫 번째 원을 K=3(원 안에 3개의 도형이 존재)이라고 하면 K=3 안에는 빨간 삼각형이 2개, 파란 사각형이 1개이므로 투표에 의해 초록색 원은 빨간 삼각형이라고 분류가 된다. 반면 K=5일 때는 빨간 삼각형이 2개, 파란 사각형이 3개이므로 초록색 원은 파란 사각형이라고 분류가 된다.

이처럼 투표에 의해 이미지 분류되는 방식을 K-Nearest Neighbors라고 한다.

위의 그림에서 볼 수 있듯 K는 커질수록 좋은 결과가 나온다. K=1일 경우를 보면 초록색 영역에서 섬처럼 노란색으로 표시되거나 빨간색 영역이 발가락처럼 생기는 등 경계선이 부드럽지 않다는 것을 볼 수 있다(일반화되지 않음). K=5인 경우는 경계들이 K=1일 때보다 부드럽게 설정된 것(보다 일반화됨)을 볼 수 있다.

CIFAR10을 KNN 분류기로 사용하여 이미지를 분류하면 위의 그림과 같이 나온다고 해보자. 빨간색 사각형은 틀리게 분류한 것이고, 초록색 사각형은 맞게 분류한 것이다. 4열의 개구리의 경우, K=1일 때 개구리는 고양이로 분류가 된다. K=4라면 고양이와 개구리가 2개씩 나오므로 개구리는 고양이나 개구리로 분류가 된다. (이 경우는 어떻게 해결해야 할까?)

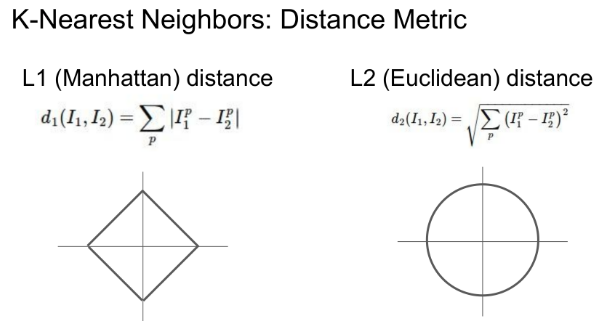
KNN 분류기에서는 Distance Metric을 L1 distance 나 L2 distance 중 하나를 선택한다. L1 distance의 경우는 좌표계가 바뀌면 거리가 달라지나 L2 distance는 좌표계가 달라져도 거리가 달라지지 않는다.

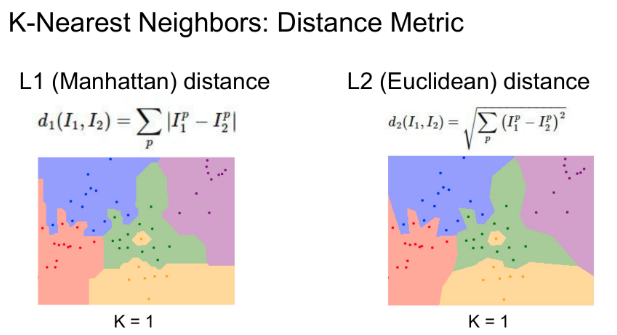
여기서는 L2 distance를 사용하는 것이 영역 경계가 더 부드럽게 나온다.

• Demo Time : 다양한 상황에서 영역이 어떻게 변화하는지 볼 수 있다.
  http://vision.stanford.edu/teaching/cs231n-demos/knn/

Hyperparameters

Hyperparameters 는 KNN 분류기에서 'K의 개수'나 '어떤 거리(L1/L2)'를 선택하는 것이다. 분류기를 설정할 때 Hyperparameters를 정해야 하는데, 이는 문제나 상황에 따라서 결과가 달라지기 때문에(문제 의존적) 모든 Hyperparameter들을 시도해보고 최상의 결과가 나오는 것을 선택해야 한다. (오토(Auto) ML을 써서 Hyperparamter를 찾을 수도 있다. 오토 DL도 있으나 아직 상용화되지 못했다. 그러나 혼자서 공부하는 대부분의 경우는 Hyperparameter를 직접 세팅한다. 참조: https://it.donga.com/27328/)

Distance Metric의 경우, L2 distance를 주로 사용하지만 키나 몸무게처럼 특정한 의미가 있는 때는 L1 distance를 사용하기도 한다.

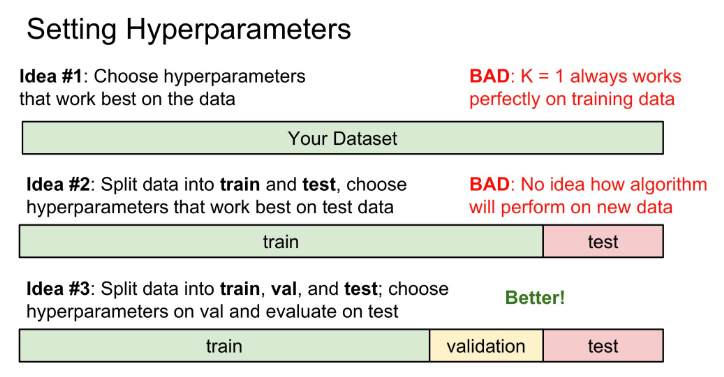
Hyperparameter를 정하는 방법은 여러 가지가 있다. 첫 번째의 경우에는 새로운 데이터에 적용할 수 없으므로 좋지 못한 결과(overfittng)가 나온다. 두 번째의 경우에도 검증 과정이 없으므로 어떻게 알고리즘이 적용되는지 알 수 없어서 좋지 않다. 3번째의 경우는 train-validation-test로 데이터를 분류하고 다양한 Hyperparameter로 train을 하고 validation에서 검증한 후 최적의 Hyperparameter를 선택하여 맨 마지막에 오직 한 번만 test한다. 이 방식이 Hyperparameter를 선택하는데 주로 사용된다.

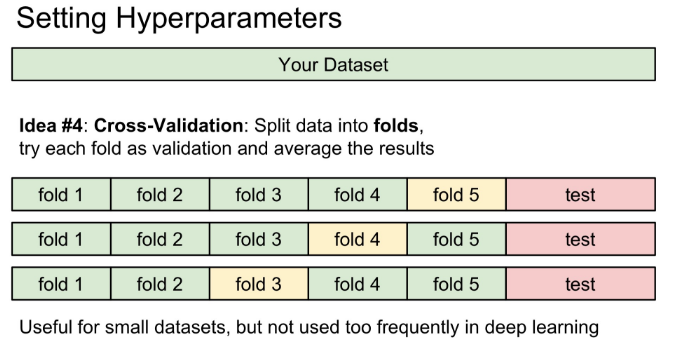
마지막 방법인 Cross-Validation 은 데이터를 여러 개로 나눈 후 train과 validation을 바꿔가면서 학습-검증을 하여 최적의 hyperparameter를 찾은 후 테스트한다. 그러나 이 방식은 딥러닝에서 자주 사용되지 않는데, 그 이유는 데이터 세트가 많은 딥러닝에서는 계산량이 많아 비용면에서 비효율적이기 때문이다. 데이터를 모으기 힘든 의료 데이터와 같이 작은 데이터의 경우에만 유용하다.

• 참고: https://machinelearningmastery.com/evaluate-performance-deep-learning-models-keras/

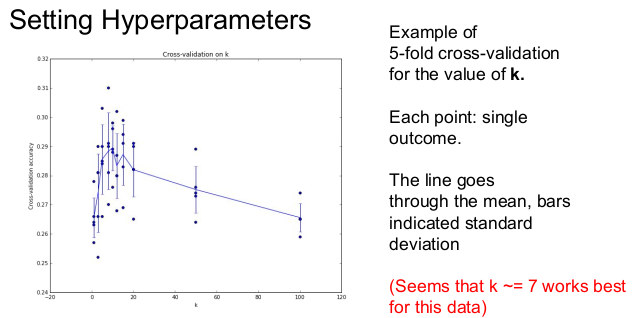
위의 그림은 5-fold cross-validation을 한 결과인데, k=7일 때 가장 최상의 결과를 나타냄을 보여준다(그래프가 가장 높이 올라간 곳이 K=7).

결론

KNN 분류기는 이미지 분류에서 절대 사용하지 않는다. 그 이유는 다음과 같다.

• 테스트 시간이 매우 느리다.
• 거리 척도들(L1/L2)이 이미지 간 '지각적 유사성'을 측정하는 척도로 적절하지 않다.
  : 색을 바꾸거나 물체를 이동해도 L2 distance를 사용하면 같은 이미지로 인식할 수도 있다.
• 차원의 저주(Curse of dimensionality)
  
  데이터가 공간을 조밀하게 채워야 하는데, 동일한 데이터라도 차원이 늘어나면 빈 곳이 (기하학적으로) 많이 생긴다. 현실에서는 많은 데이터를 구하기 힘들고, 차원이 데이터보다 높을 경우 문제가 생긴다.
• 참고문헌 : https://datapedia.tistory.com/15

Linear Classification

Linear classifier는 간단하지만 신경망(Neural Network)에서 기본이 되는 블록이다.

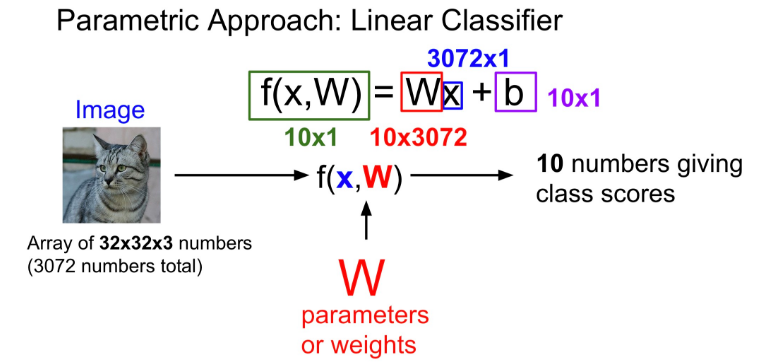
Parametric Approach는 KNN 분류기와 달리 외우지 않고 parameter를 결정하여 이미지를 분류한다. 따라서 KNN 분류기보다 이미지 분류 시간이 적게 걸린다. 위의 그림에서 x는 입력 이미지(고양이)이고 W는 가중치 혹은 파라미터 라고 한다. Parametric Approach에서는 가중치 W를 학습하고 x와 W를 조합하여 함수를 만들어 이미지를 분류한다. 그중 가장 간단한 방법이 x와 W를 곱하는 Linear classification이다(W를 구하는 것이 우리의 관심사이다).

f(x, W) 함수에서 b는 bias이며 bias는 학습과 무관한 특정 클래스에 대한 선호도이다. 예를 들어 고양이 데이터가 개 데이터보다 많으면 고양이 클래스에 대한 bias가 더 커진다.

이미지를 넣으면 머신러닝에서 f(x, W) 함수를 학습한 후 클래스마다 예측되는 점수를 준다. 위의 그림에서는 10개의 클래스이므로 예측 점수 10개가 주어진다.

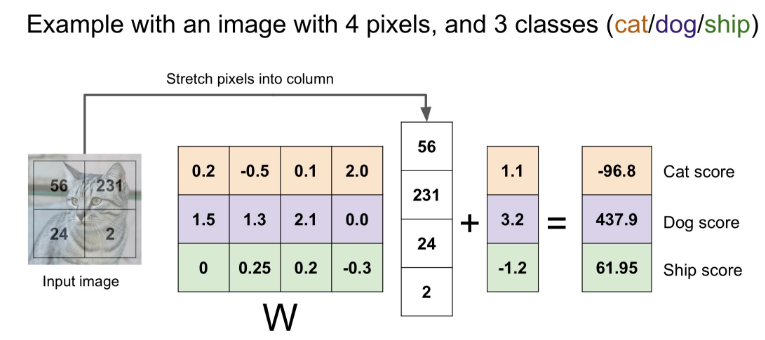
4 pixel의 이미지를 고양이, 개, 배의 3가지 클래스로 분류한다고 해보자. 이 Linear classifier는 2×2 이미지를 입력으로 받고, 이미지를 4열 벡터로 펼친다. 가중치 행렬 W의 각 행은 각 클래스에 대한 템플릿이라고 할 수 있다. W의 행 벡터와 이미지의 열벡터의 내적을 구하고 bias를 더하여 3개의 클래스에 대한 점수가 나온다. 여기서는 개 클래스의 점수가 가장 높게 나오므로 이 Linear classifier는 입력한 고양이 이미지를 개로 분류함을 알 수 있다.

위의 그림에서 아래에 보이는 10개의 이미지는 가중치 W의 템플릿을 시각화한 것이다. 이 이미지들은 Linear classifier가 데이터를 어떻게 바라보는지를 알려준다.

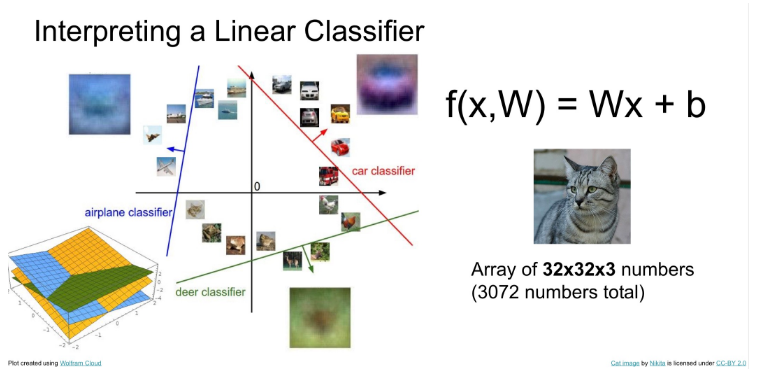
Linear classifier의 다른 해석 방법으로는 각 이미지를 한 점으로 생각하고 f(x, W) 함수를 선으로 그리는 것이다. 파란선 왼편으로는 비행기라고 분류하고 초록색 선 아래로는 사슴이라고 분류한다.

그러나 한 클래스에는 한 템플릿만을 가지고 있기 때문에 한계가 있다. 한 클래스 내에 다양한 특징이 있더라도 그 특징이 무시되는 것이다. 예를 들면 이 분류기는 자동차 클래스가 붉은색에 파란 유리창을 가지고 있다고 생각하기 때문에 노란색 자동차는 자동차로 분류하지 않을 것이다.

한계

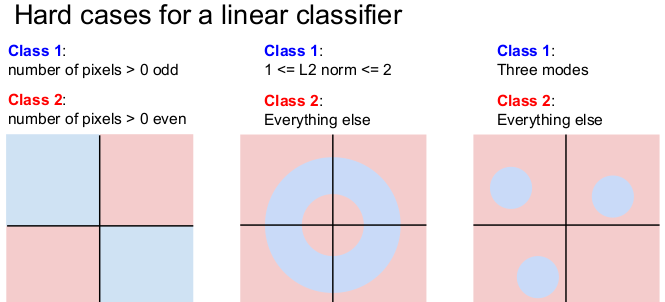
Linear claissfier는 간단하지만 이 분류기로 분류하기 힘든 경우가 있다. Linear Classifier는 선 하나를 그어 이미지를 분류해야 하는데, 왼쪽 그림과 같은 parity problem이나 오른쪽 그림 같은 Multimodal problem의 경우는 선 하나로 뷴류하기 힘들다.

• 참고문헌: https://leechamin.tistory.com/85?category=830805
  https://younnggsuk.github.io/2020/12/03/cs231n-3.html