Attention Mechanism
RNN에 기반한 seq2seq 모델에는 두 가지 문제점이 있다.
- 고정된 크기의 벡터(콘텍스트 벡터)에 모든 정보를 압축하기 때문에 정보 손실이 발생한다. (오래된 정보부터 손실이 일어난다.)
- RNN의 특성 때문에 기울기 소실 문제가 있다.
입력 시퀀스가 길어지면 출력 시퀀스의 정확도가 떨어지므로 어텐션이 나타났다.
어텐션의 아이디어
입력 시퀀스를 한 번에 입력하고, 디코더에서 출력 단어를 예측하는 매 시점마다 전체 입력 문장을 다시 참고한다. 전체 문장을 동일하게 참고하는 것이 아니라 예측해야 하는 단어와 연관이 있는 입력 단어 부분에 조금 더 집중한다는 점을 유의해야 한다.
어텐션 모델
어텐션 모델(seq2seq + 어텐션 값 계산)인 모델이다. 어텐션 모델에서 중요한 것은 어텐션 값을 어떻게 구하는가 이다. 즉 어텐션 값을 구하는 어텐션 스코어 함수만 다를 뿐 기본 매커니즘은 비슷하다. 아래는 여러 종류의 어텐션 스코어 함수이다.

(: Query, : Keys, : 학습 가능한 가중치 행렬)
여기서는 3가지만 설명한다.
- 닷-프로덕트 어텐션(Dot-product Attention) - 루옹 어텐션 중 하나
- 바다나우 어텐션(Bahdanau Attention - Global Attention) - concat 어텐션
- 루옹 어텐션(Luong Attention - Local Attention)
디코더의 현재 시점 t에서 출력 단어를 예측하기 위해 디코더의 셀은 1) 이전 시점의 t-1에서의 은닉 상태, 2) 이전 시점 t-1에서 나온 출력 단어, 3) 어텐션 값 이 필요하다. 이제부터 각각의 어텐션을 사용하여 디코더에서 출력 단어를 예측하는 과정을 상세히 설명한다.
Dot-Product Attention
닷-프로덕트 어텐션을 이해하기 위해서는 먼저 쿼리(Query), 키(Key), 값(Value)를 이해해야 한다. (참고로 아래에서 사용되는 은닉 상태라는 것은 은닉 상태 벡터이다.)
- Q = Query: t 시점의 디코더 셀에서의 은닉 상태
- K = Keys: 모든 시점의 인코더 셀의 은닉 상태들
- V = Values: 모든 시점의 인코더 셀의 은닉 상태들
어텐션 함수는 주어진 쿼리에 대해 모든 키와의 유사도(어텐션 스코어)를 각각 구하고, 이 유사도를 키와 매핑된 각각의 값에 반영한 후, 그 유사도가 반영된 값(어텐션 값, Attention Value)을 모두 더해 리턴한다. (행렬로 한 번에 계산하면 더하는 과정은 생략된다. 아래의 식에서 Q, K, V는 행렬이다.)

위의 그림은 디코더의 세 번째 LSTM 셀에서 출력 단어를 예측할 때 어텐션 매커니즘을 사용하는 모습이다. 여기서 중요한 것은 인코더의 소프트맥스 함수 이다. 소프트맥스 함수를 통해 나온 결과값은 입력 시퀀스의 단어 각각이 출력 단어를 예측할 때 얼마나 도움이 되는지를 수치화한 값(어텐션 분포, Attention Distribution)이다. 이를 하나의 정보로 담아(초록색 삼각형, 어텐션 값, Attention Value) 디코더로 전송되면 디코더는 출력 단어를 정확하게 예측할 확률이 높아진다.
인코더의 모든 은닉상태와 t시점에서의 디코더의 은닉상태 내적(어텐션 스코어)-> 모든 어텐션 스코어는 소프트맥스 함수 통과(어텐션 분포) -> 어텐션 분포의 각 값(어텐션 가중치)과 인코더의 모든 은닉상태를 곱한 값을 모두 더함(어텐션 값) -> 어텐션 값과 디코더의 t시점에서의 은닉상태를 연결(concat)한 값을 가중치 행렬과 곱하고 tahn 함수를 통과 -> 앞에서 구한 값을 dense 층과 softmax를 지나게 해 예측 벡터 얻음
1. 어텐션 스코어(attention score) 구하기
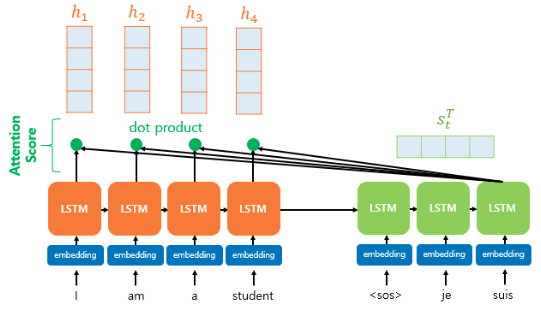
- : 인코더의 은닉 상태 (i=1, 2, ..., n)
- : 현재 시점(time step) t에서의 디코더의 은닉 상태
어텐션 값을 구하기 위해서는 먼저 어텐션 스코어를 구해야 한다. 어텐션 스코어는 현재 디코더의 시점 t에서 단어를 예측하기 위해 인코더의 모든 은닉 상태가 디코더의 현 시점의 은닉 상태 와 얼마나 유사한지 판단한다.
와 는 열벡터이므로 디코더의 은닉 상태 를 전치하고 각 은닉 상태와 내적을 수행하여 어텐션 스코어 값(스칼라)을 얻을 수 있다. 이 어텐션 스코어 값을 모두 모은 것을 라고 하자.
Attention score = 디코더의 현재 시점 t에서의 은닉상태와 인코더의 모든 은닉 상태의 내적. 인코더의 각 은닉 상태가 현재 시점의 디코더의 은닉 상태와 얼마나 유사한지의 정도
2. 어텐션 분포(Attention Distribution) 구하기
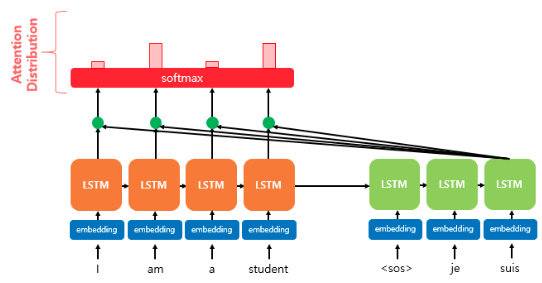
어텐선 스코어 에 소프트맥스 함수를 적용하면 어텐션 분포(확률 분포)를 얻을 수 있다. 어텐션 분포의 각각의 값을 어텐션 가중치(attention weight) 라고 하자.
Attention Distribution: 모든 어텐션 스코어에 softmax를 씌워서 나온 확률 분포, 어텐션 가중치의 모음값
Attention Weight: 어텐션 분포의 각각의 값
3. 어텐션 값(Attention Value) 구하기
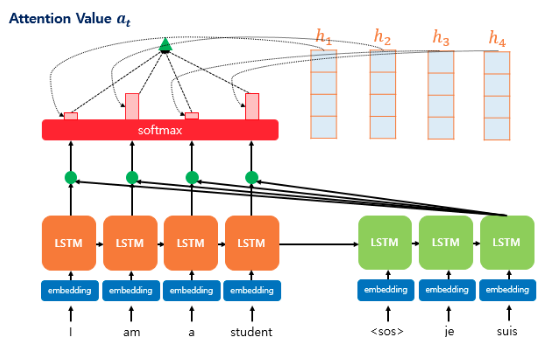
어텐션 값 을 구하기 위해 인코더의 각 은닉 상태와 어텐션 가중치값을 곱한 후, 모두 더한다. 어텐션 값은 인코더의 문맥을 포함하고 있기 때문에 컨텍스트 벡터(context vector)라고 불린다.
Attention Value: 인코더의 각 은닉 상태와 어텐션 가중치값을 곱한 후, 모두 더한 값, 컨텍스트 벡터
4. 어텐션값과 디코더의 현재 시점의 은닉 상태 연결하기

어텐션 값 와 디코더의 현재 시점 은닉상태인 를 결합(concatenate)하여 하나의 벡터 를 만든다.
5. 출력층 연산의 입력 계산하기
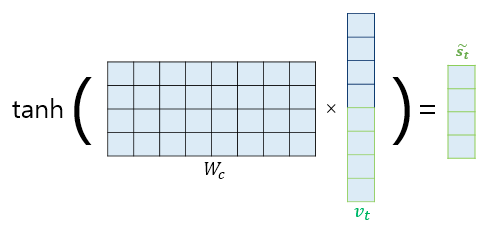
와 가중치 행렬 을 곱한 후 tanh 함수를 지난 후에 출력층 연산을 위한 벡터 을 얻는다.
예측 벡터 얻기
을 출력층의 입력으로 하여 예측 벡터를 얻는다. 즉 는 Dense층과 softmax를 지나 예측 벡터가 된다.
Bahdanau Attention
바다나우 어텐션을 이해하기 위해서는 먼저 쿼리(Query), 키(Key), 값(Value)를 이해해야 한다.
- Q = Query: t-1 시점의 디코더 셀에서의 은닉 상태
- K = Keys: 모든 시점의 인코더 셀의 은닉 상태들
- V = Values: 모든 시점의 인코더 셀의 은닉 상태들
닷-프로덕트 어텐션과 달리 바다나우 어텐션에서의 쿼리는 이전 시점 t-1에서의 은닉 상태 임을 유의해야 한다.
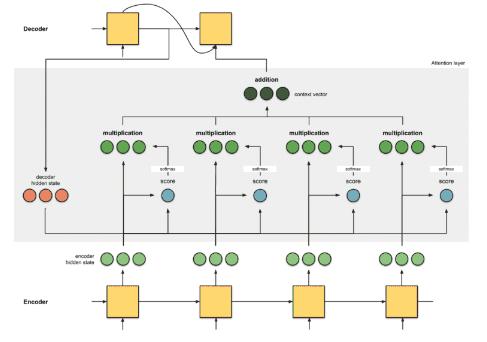
[출처: https://eda-ai-lab.tistory.com/157]
1. 어텐션 스코어 구하기
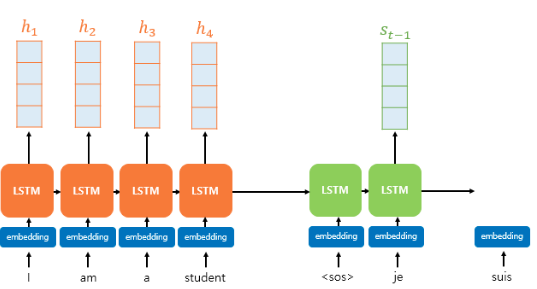
- : 인코더의 은닉 상태 (i=1, 2, ..., n)
- : 이전 시점(time step) t-1에서의 디코더의 은닉 상태
바다나우 어텐션의 어텐션 스코어 함수는 아래와 같다.
(: 학습 가능한 가중치 행렬, H: 각 를 열벡터로 만든 행렬)
각각의 은닉 상태에서 구해진 어텐션 스코어를 모두 합한 것이 이다. (여기서는 행렬로 구했기 때문에 위에서 구한 어텐션 스코어가 바로 이다.)
2. 어텐션 분포 구하기
에 소프트맥스 함수를 적용해 어텐션 분포를 구하며, 각각의 값은 어텐션 가중치(Attention Weight)이다.
Attention Weight: 디코더의 RNN이 를 선택할 때 인코더의 은닉 상태를 얼마나 이용할 것인지를 결정한다. 신경망에 의해 학습된다.
3. 어텐션 값 구하기
각 인코더의 은닉 상태와 어텐션 가중치값을 곱한 후 모두 더한 값이 어텐션 값이다. 이 벡터는 인코더의 문맥을 포함하므로 컨텍스트 벡터 라고 부른다.
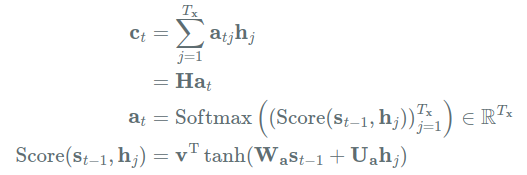
4. 컨텍스트 벡터로부터 새로운 은닉 상태 구하기

컨텍스트 벡터와 현재 시점의 입력인 단어의 임베딩 벡터를 연결(concatenate)한 것과 이전 시점의 셀로부터 전달 받은 은닉 상태 로부터 새로운 은닉 상태 가 나온다.
디코더의 현재 시점의 은닉 상태 = 현재 시점의 컨텍스트 벡터 , 이전 시점의 은닉 상태 , 현재 시점의 입력 가 사용됨
Attention Weight Matrix
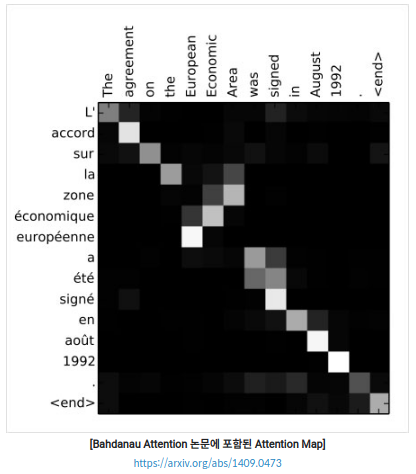
위의 그림은 단어끼리의 어텐션 가중치를 표현한 것이다. 흰 색일수록 높은 어텐션 가중치이다. 그림에서 관사끼리 서로 연결되어 있는 것을 볼 수 있고, 의미가 비슷한 단어끼리 높은 어텐션 가중치를 가진다. 하나의 단어가 두 개 이상의 단어 정보를 조합해 이용하기도 한다.
그러나 한 단어 를 만들기 위해 이용되는 인코더의 은닉 상태는 많지 않다. 즉 디코더는 컨텍스트를 선택적으로 이용한다.
Luong Attention
 [출처: https://hcnoh.github.io/2019-01-01-luong-attention]
[출처: https://hcnoh.github.io/2019-01-01-luong-attention]
- Luong Attention의 연산
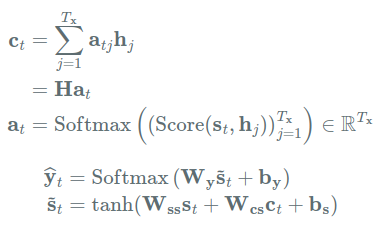
(: 컨텍스트 벡터, : 어텐션 가중치값, : 예측값)
바다나우 어텐션과 루옹 어텐션의 차이
- 컨텍스트 벡터
- 바다나우: 컨텍스트 벡터를 구할 때 이전 시점의 은닉 상태 를 사용한다.
- 루옹: 컨텍스트 벡터를 구할 때 현재 시점의 은닉 상태 를 사용한다.
- 출력
- 바다나우: 현재 시점의 은닉 상태 로부터 출력이 나온다.
- 루옹: 현재 시점의 은닉 상태 는 RNN의 은닉 상태 역할만 하고, 새로운 벡터 를 사용한다.
- computation path
- 바다나우: 디코더의 은닉 상태 를 구할 때 컨텍스트 벡터가 사용되므로 RNN의 재귀 연산이 수행될 때 컨텍스트 벡터가 구해질 때까지 기다려야 한다.
- 루옹: 출력을 구하는 부분과 RNN의 재귀 연산 부분이 분리되어 계산이 빨라졌다.
- 인코더의 은닉 상태 사용
- 바다나우: 인코더의 모든 은닉 상태의 벡터를 본다.
- 루옹: 특정 하이퍼파라미터 D에 대해 (2D+1)개의 부분집합 벡터만 본다.
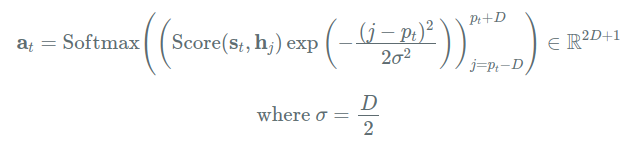
위의 식에서 은 Aligned Position이고, 를 구하는 방식에 따라 Local Attention의 방법이 달라진다.
- Monotonic Alignment (local-m):
- Predictive Alignment (local-p):
구해진 와 범위 에 대해 Weighted sum(가중치와 곱하고 더함)을 통해 컨텍스트 벡터 를 구한다.
- 어텐션 스코어 함수
-
바다나우:
(: 학습 가능한 가중치 행렬, H: 각 를 열벡터로 만든 행렬) -
루옹:

Local-Based Function은 어텐션이 필요하다. 4개의 함수 중 가장 합리적인 성능을 보이는 함수는 general이다.
- Input Feeding Approach
- 바다나우: 은닉 상태 에 현재 시점의 입력 만 들어간다.
- 루옹: 은닉 상태 에 현재 시점의 입력 이 이전 시점의 새로운 은닉 상태 벡터 와 concatenate되어 들어간다. 이전의 alignment 정보를 폭넓게 사용할 수 있고 네트워크를 수직/수평으로 넓게 구현했다는 장점이 있다.
성능비교
Global Attention < Local-m < Loca-p
참고 자료
https://wikidocs.net/22893
https://wikidocs.net/73161
https://katie0809.github.io/2020/02/23/ai-study7/
https://eda-ai-lab.tistory.com/157
https://hcnoh.github.io/2019-01-01-luong-attention
- 출처가 없는 그림은 위키독스에서 가져왔습니다.
- 정리했는데도 계속 혼동되는 이유가 뭘까요? 앞으로 자주 봐야겠습니다.
