SVD(특이값 분해)

특이값 분해

특이값 분해는 m x n 크기의 임의의 사각 행렬 A를 특이 벡터(Singular vector)의 행렬과 특이값(Singular value)의 대각 행렬로 분해하는 것이다.

• 특이값 분해를 하는 이유와 그 의미

1. 행렬의 크기 감소
2. 정방행렬이 아닌 행렬의 해를 구할 수 있다.
3. 데이터의 크기를 줄여준다.

특이값 분해를 하면 모든 성분이 가치가 높은 순으로 정렬되어 분해된다. 가치가 낮은 부분은 truncate로 제거, 그리고 다시 복원한다.

SVD의 식

$A=UΣV^T$

• Σ: 대각성분이 양수인 대각행렬, 큰 수부터 작은 수 순서로 배열됨. $Σ \in \mathbf {R}^{NxM}$
• U: N차원 정방행렬, 모든 열벡터가 단위벡터이고 서로 직교한다. $U \in \mathbf {R}^{NxN}$
• V: M차원 정방행렬, 모든 열벡터가 단위벡터이고 서로 직교한다. $V \in \mathbf {R}^{MxM}$

위 조건을 만족하는 행렬 Σ의 대각성분들을 특이값 (singular value), 행렬 U의 열벡터들을 왼쪽 특이벡터 (left singular vector), 행렬 V의 행벡터들을 오른쪽 특이벡터(right singular vector)라고 한다.

특이값 분해 행렬의 크기

만약 N>M이면 Σ 행렬이 M개의 특이값(대각성분)을 가지고 다음처럼 아랫 부분이 영행렬이 된다.

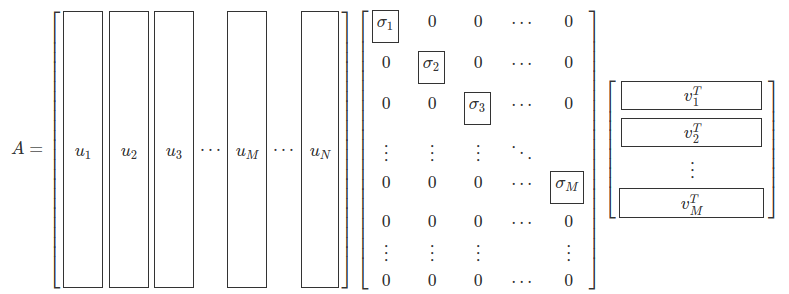
[출처: 3.4 특잇값 분해]

N<M이면 Σ 행렬이 N개의 특이값(대각성분)을 가지고 다음처럼 오른쪽 부분이 영행렬이 된다.

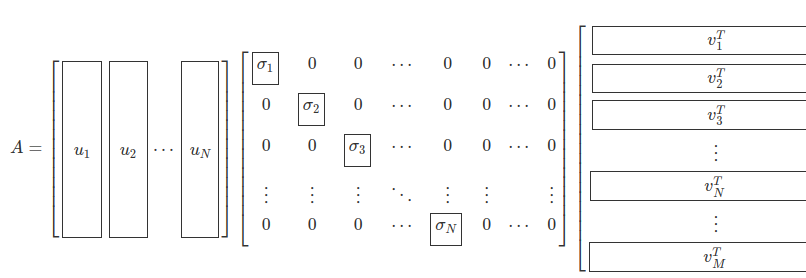
[출처: 3.4 특잇값 분해]

특이값 분해의 축소형(Truncated SVD)

특잇값 가운데 가장 큰(가장 중요한) t개만 남기고 해당 특잇값에 대응되는 특이행렬(singular vector) 로 행렬 A를 근사(approximate)한 것을 절단적 특잇값 분해(Truncated SVD) 라고 한다.

특잇값 대각행렬에서 0인 부분은 의미가 없기 때문에 대각행렬의 0 원소 부분과 이에 대응하는 왼쪽(혹은 오른쪽) 특이벡터들을 없애도 원래 행렬이 나온다.

N이 M보다 큰 경우에는 왼쪽 특이벡터 중에서 $u_{M+1},⋯,u_N$을 없앤다.

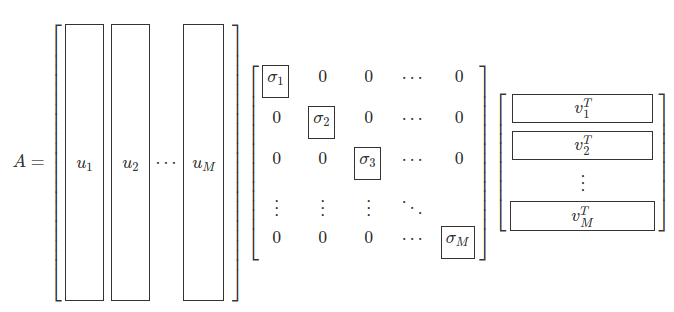
[출처: 3.4 특잇값 분해]

N이 M보다 작은 경우에는 오른쪽 특이벡터 중에서 $v_{N+1},⋯,v_M$을 없앤다.

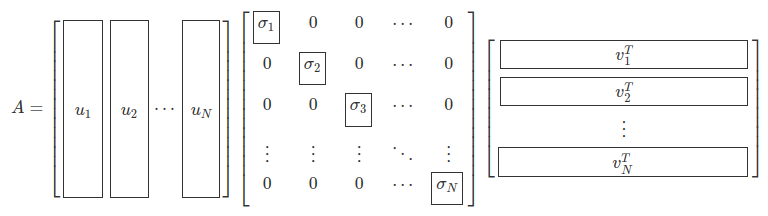
[출처: 3.4 특잇값 분해]

Truncated SVD를 수행하면 행렬 Σ의 대각 원솟값 중에서 상윗값 t개만 남고 U행렬과 V행렬의 t열까지 남는다. 이로 인해 세 행렬에서 값(정보)의 손실 이 일어나 기존의 행렬 A를 정확히 복구할 수는 없다. 여기서 t는 하이퍼파라미터(사용자가 직접 값을 선택하며 성능에 영향을 주는 매개변수)이다. t를 크게 잡으면 기존의 행렬 A로부터 다양한 의미를 가져갈 수 있지만, 노이즈를 제거하려면 t를 작게 잡아야 한다.

• 참고문헌
  AIFFEL 대전 Going Deeper 노드
  3.4 특잇값 분해
  특이값 분해 ( SVD ) 매트랩 예제 및 쉬운 이해! Singular value decomposition 의 목적