[무갇수] 행렬과 연립방정식

시작 전에 슬랙에 올라온 강의 노트를 보았는데도 소거법에 대한 것은 이해가 안 되었다. 결국 블로그를 참고해 소거법을 대충이라도 보고 가니 이해가 되었다. 스터디가 시작하자 J님께서 소거법에 대해 설명해주시고 50분간 수학 문제를 풀었다.

오늘의 문제도 10문제인데, 문제지가 꽉 차 있어서 뭔가 부담스러웠다. 처음에 조금 헤매다가 감을 잡고 문제를 풀기 시작했다. 계산에 분수가 나오니 혼란스러워서 2번씩 푼 것도 있다. 50분을 꽉 채웠지만 10-3번 문제는 못 풀었다. 내일 답을 올려주시면 알 수 있으려나.

10시 10분부터 J님이 고유값과 고유벡터에 대해 이야기하시면서 6-2번 문제가 고유값과 관련된 문제라고 하셨다. 고유값까지는 이해했지만 고유벡터의 경우는 말로만 설명을 들으니 이해가 잘 안 되었다. 코사인과 내적에 대한 것도 설명해 주셨지만 머리가 멍해 한 귀로 듣고 한 귀로 흘려보냈다. 나중에 벡터의 내적 공부할 때 다시 언급하신다니 그 때 이해해야겠다.

아래의 내용은 J님께서 올려주신 강의 노트의 내용을 정리한 것이다.

두 직선 사이의 위치 관계

• 도형을 식으로 표현하는 2가지 방법

1. $y = f(x)$
2. $f(x, y) = 0$

• x값 하나에 y값 하나가 대응되는 것이 (1차) 함수이다.

한 평면 위에서 두 직선의 관계

두 직선 $y = m_1x + n_1$와 $y = m_2x + n_2$가 존재할 때, 두 직선의 관계는 다음과 같다.

1. $m_1 \neq m_2 \Leftrightarrow$ 한 점에서 만난다. (한 쌍의 해)
   $m_1m_2 = -1 \Leftrightarrow$ 수직으로 만난다. (직교, 한 쌍의 해)
2. $m_1 = m_2, n_1 \neq n_2\Leftrightarrow$ 평행 (불능)
3. $m_1 = m_2, n_1 = n_2 \Leftrightarrow$ 일치(부정)

연립 방정식

앞으로 다룰 연립방정식은 1차 연립방정식이며, 구하는 값이 n개 이면 n원 일차 연립방정식이라고 한다. 계수와 변수가 모두 실수인 n원 일차연립방정식의 해는 n개의 직선이 만나는 교점의 좌표이다.

• 연립방정식을 행렬로 표기
  

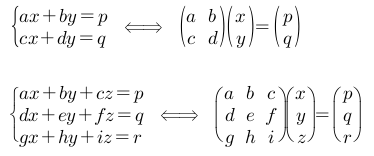
• 역행렬을 이용한 연립일차방정식의 풀이
  

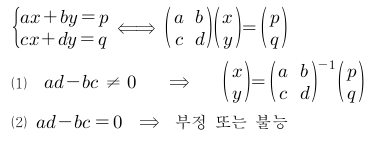
역행렬의 존재 여부는 직선의 기울기가 같은지 판별하는 것과 같다.

• 소거법(오늘 스터디의 핵심!)
  

• 참고: 가우스 소거법과 행렬법

  행렬식의 성질

  1. 행과 열에 어떤 수를 더하거나 빼주어도 행렬식의 값은 변화가 없다.
  2. 행/열끼리 교환하면 행렬식의 부호는 반대가 된다.
     상삼각행렬: 대각선을 기준으로 아래의 모든 요소가 0인 행렬

• 행렬의 성질을 이용해서 소거법을 사용할 수 있다. 소거법을 통해 연립방정식의 해와 역행렬을 구할 수 있다.

• 고유값과 고유벡터
  오늘 푼 6번 문제와 관련된 개념. J님이 설명해 주셨는데 이해가 안 된다.

• 나중에 볼 것: [선형대수학 #3] 고유값과 고유벡터 (eigenvalue & eigenvector)
  고윳값과 고유벡터

• 코사인과 내적?