[풀잎스쿨] CS231n 7강 Training Neural Networks Part 2 (2)

데이터 여행자·2021년 2월 20일

[AIFFEL 대전 1기] 학습일지

목록 보기

22/42

스탠퍼드 대학의 CS231n: Convolutional Neural Networks for Visual Recognition
본 포스팅은 CS231n의 내용을 정리한 것이다. 이곳에 출처가 따로 언급되지 않은 이미지들은 스탠퍼드 대학에서 제공하는 강의 슬라이드에서 가지고 왔다.
[CS231n] http://cs231n.stanford.edu/2017/syllabus.html

Optimization: Adam

지금까지 velocity를 이용해서 step을 조절하는 momentum이라는 방법과 gradients의 제곱을 나눠주는 방식으로 step을 조절하는 AdaGrad와 RMSProp을 알아보았다. 이 둘은 모두 괜찮은 아이디어이므로 이 두 방법을 조합하면 더 좋은 결과가 나오지 않을까 하는 생각에서 출발한 것이 Adam이다. Adam의 현재 식이 나오게 된 과정을 먼저 살펴보자.

위의 식은 Adam과 "유사한" 알고리즘이다. Adam은 first moment와 second moment을 이용해 이전의 정보(estimate)를 유지시킨다. 빨간색 first moment는 gradient의 가중합이고, 파란색 second moment는 AdaGrad이나 RMSProp처럼 gradients의 제곱을 이용하는 방법이다.

이 Adam(almost)으로 Update를 진행하면 first moment는 velocity를 담당하고 sqrt(second moment)로 나눠주는데, 여기서 second moment는 gradient의 제곱항이다. Adam(almost)은 "RMSProp + momentum" 같아 보인다. 즉 "momentum + second squared gradients"이다. RMSProp와 momentum의 유용한 특징을 모두 이용하는 것이다.

하지만 문제가 하나 있다. 초기 step 에서는 어떤 일이 발생할까? 먼저 초기 step에서 second moment를 0으로 초기화한다. second moment를 1회 업데이트하면, beta2는 decay_rate(0.9또는 0.99)로 1에 가까운 값이다. 따라서 1회 업데이트 후에도 second moment는 여전히 0에 가깝다. update step에서 second moment로 나누면 나눠주는 값이 크기 때문에 초기 step이 엄청나게 커진다. 중요한 것은 이 커진 step이 실제로 손실함수가 가파르기 때문이 아니라 second moment을 0으로 초기화시켰기 때문에 발생하는 '인공적인' 현상이라는 것이다.

first moment도 초기에 엄청 작은 값일 것이다. 따라서 learning rate에 '엄청 작은 값'을 곱하고(first moment) '엄청 작은 값의 제곱근(second)'을 나누면 어떻게 될까? 어쩌면 서로 상쇄될 수도 있지만 엄청 큰 step이 발생할 수도 있다. 제대로 초기화를 해주지 않아서 아주 큰 step이 발생했다면 아주 엉뚱한 곳으로 이동할 수도 있고, 그 결과 수렴하지 못할 수도 있다.

Q. 수식의 10^-7이 무엇인가?
현재 나눗셈을 하고 있기 때문에 분모가 0이 되지 못하게 분모에 작은 양수 값(10^-7)을 더해준다. 보통 10^-7이나 10^-8정도를 사용하면 된다.

Adam은 이를 해결하기 위해 보정하는 항인 "bias correction term"을 추가한다. first/second moments를 Update하고 난 후 현재 Step에 적절한 unbiased term을 넣어준다. Adam은 다양한 문제들에서 잘 동작하므로 일반적으로 Adam을 사용하면 된다. beta_1 = 0.9, beta_2 = 0.999, Learning rate를 1e-3나 5e-4 정도로 설정하면 거의 모든 아키텍쳐에서 잘 동작하는 시작점이 될 것이다.

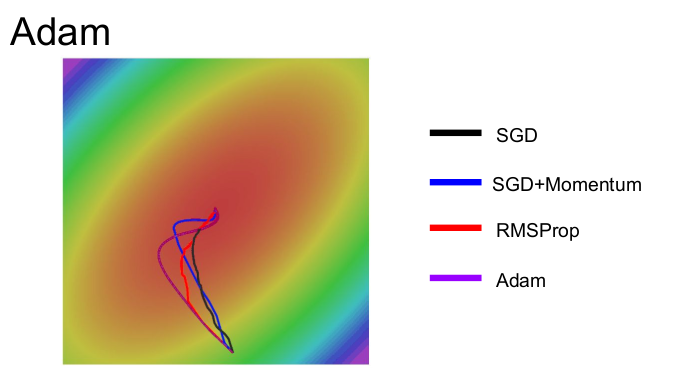
동일한 환경에서 SGD, Momentum, RMSProp, Adam을 비교해 보자. 보라색 Adam은 momentum과 RMSProp을 합쳐놓은 모습이다. Adam이 momentum처럼 overshoot하지만 momentum만큼 심하지 않다. 또한 Adam은 RMSProp처럼 각 차원의 상황을 따로 고려해서 Step을 이동한다.

Q. Adam이 해결하지 문제는 무엇인가?
Adam을 쓰더라도 여전히 문제점이 있다. 예를 들어 손실함수가 타원형이라고 하자. Adam을 이용하면 각 차원마다 적절하게 속도를 높히고 줄이면서 '독립적으로' step을 조절할 것이다. 하지만 Adam은 차원에 해당하는 축(수평/수직 축)만 조절할 수 있기 때문에 이 타원이 기울어져 있다면 해결하지 못한다. 그러나 회전된 타원(poor conditioning) 문제는 Adam을 비롯한 다른 여러 알고리즘들도 다룰 수 없는 문제이다.

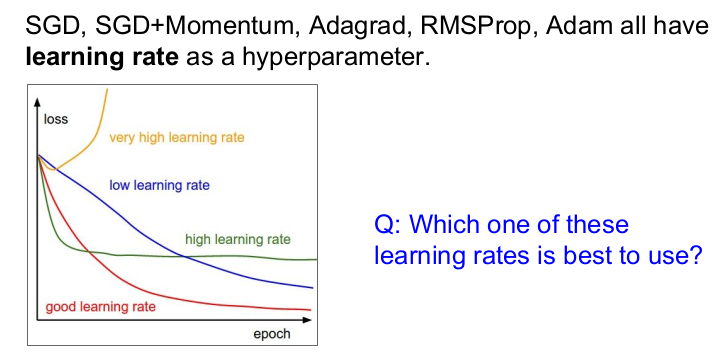
지금까지의 모든 Opimization 알고리즘은 learning rate라는 하이퍼파라미터를 가지고 있다. Learning rate가 지나치게 높으면 노란색 선처럼 솟구치고, 파란색 선처럼 너무 낮으면 수렴하는데 너무 오래걸린다. 따라서 learning rate를 잘 고르는 것은 상당히 까다롭다.

따라서 각각의 learning rates의 특성을 적절히 이용하여 learning rates dacay 전략을 사용할 수 있다. 처음에는 learning rates를 높게 설정한 다음에 학습이 진행될수록 learning rates를 점점 낮출 수 있다. step decay 방법에서는 몇 개의 epochs마다 높은 learning rates를 낮출 수 있다. exponential decay 방법으로는 학습과정 동안에 꾸준히 learning rate를 낮출 수도 있다. 그 외에도 다양한 전략이 있다.

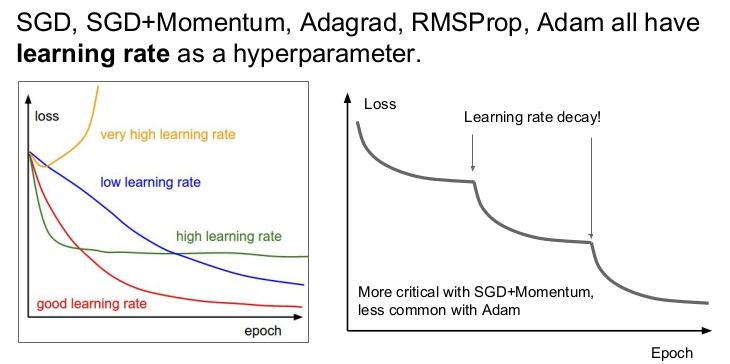
오른쪽의 그림은 Resnet 논문에 있는 그림이다. Loss가 계속 내려가다가 어느순간 평평해지더니 다시 또 내려가는 것을 반복한다. Resnet 논문에서는 step decay learning rate 전략을 사용하였다. 평평해지다가 갑자기 내려가는 구간은 Learning rate를 낮추는 구간이다. 수렴을 잘 하고 있는 상황에서 gradient가 점점 작아지면, learning rate가 너무 높아서 더 깊게 들어가지 못한다. 그 때 learning rate를 낮추면 속도가 줄어들어 계속 Loss가 내려갈 수 있다.

참고할 것은 learning rate decay는 Adam 보다는 SGD Momentum을 사용할 때 자주 쓴다는 것이다. 또한 learning rate decay는 부차적인 하이퍼파라미터이므로 학습 초기부터 고려하지는 않는다. 보통 학습 초기에는 learning rate decay가 없다고 생각하고 learning rate를 잘 선택하는 것이 중요하다. 우선 decay 없이 학습을 시키고, Loss curve를 잘 살피고 있다가 decay가 필요한 곳이 어디인지 고려해 사용하면 된다.

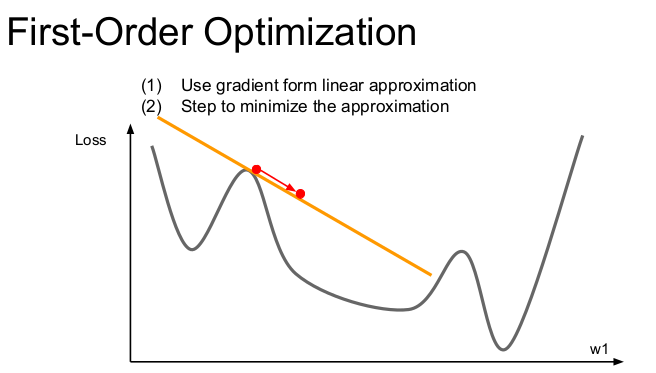
지금까지 배운 Optimization 알고리즘들을 모두 1차미분을 활용한(first-order, 1번 미분하는 것) 방법이다. 위의 그림처럼 빨간색 점에서 손실함수의 gradient를 구했다고 하자. 이 gradient 정보를 이용해서 손실함수를 선형함수로 근사(1차 테일러 근사)시킨다. 이 1차 근사함수를 실제 손실함수라고 가정하고 Step을 내려가지만 이 근사함수로는 멀리갈 수 없다.

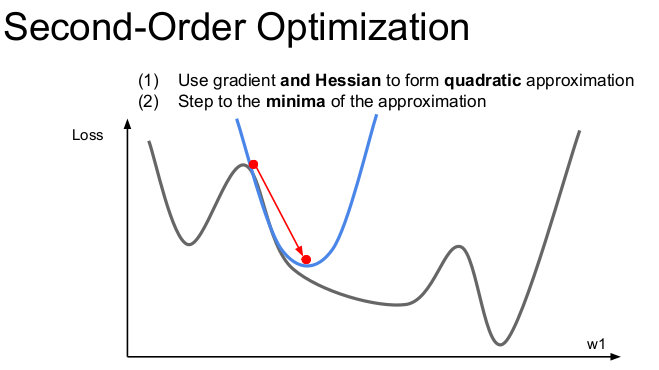
따라서 2차 근사 (second-order approximation)의 정보를 추가적으로 활용하여 minima에 더 잘 근접하도록 한다. 이것이 바로 2nd-order optimization의 기본 아이디어이다. 2차 근사를 이용한 함수는 2차 테일러 근사 함수이고, 이 함수는 2차함수의 모양을 가진다. 2차 미분한 함수는 기울기의 변화율을 알 수 있으므로 그 점이 변곡점인지, minima인지 알 수 있다.

위의 예시를 다차원으로 확장시킨 것이 'Newton step'이다. 2차 미분값들로 된 행렬인 Hessian matrix를 계산하고, Hessian matrix의 역행렬을 이용하면 실제 손실함수의 2차 근사를 이용해 minima로 바로 이동할 수 있다.

이론적으로 "Newton's method" 에서는 learning rate는 필요없고, 매 step마다 항상 minima를 향해 이동한다. 그러나 실제로는 2차 근사도 사실상 완벽하지 않기 때문에 learning rate가 필요하다. Newton's method는 minima로 이동하는게 아니라 'minima의 방향'으로 이동하기 때문이다.

어쨌든 이론적으로 Newton's method에서는 learning rate가 필요하지 않다. 그러나 안타깝게도 Newton's method는 Deep learning에서 사용할 수 없다. 왜냐하면 Hessian matrix는 N x N 행렬(N: Network의 파라미터 수)이므로 N이 1억이면 1억의 제곱만큼 존재한다. 이를 메모리에 저장할 방법은 없고 역행렬 계산도 불가능하다.

따라서 실제로는 'Quasi-Newton methods'를 이용한다. Quasi-Newton methods는 Full Hessian을 근사시킨다. 즉 Low-rank approximations 하는 방법이다.

L-BFGS도 Hassian을 근사시켜서 사용하는 방법이다. 그러나 L-BFGS도 DNN에서는 잘 사용하지 않는다. 왜냐하면 L-BFGS에서 2차근사가 stochastic case에서 잘 동작하지는 않고 non-convex 문제(참고: Convex 최적화(1): Convex Function, Set)에도 적합하지 않기 때문이다. (?)

하지만 full batch update가 가능하고 확률성(stochasticity)이 적은 경우에는 L-BFGS가 좋은 선택일 수도 있다. L-BFGS가 Neural network를 학습시키는데 많이 사용되지 않지만 Style tranfer와 같은 알고리즘에서는 L-BFGS을 종종 사용한다. (Style tranfer같은 stochasticity와 파라미터가 적을 때 Optimization을 해야할 경우)

실제로는 Adam을 제일 많이 쓴다.

optimization 알고리즘은 training error를 줄이고 손실함수를 최소화시키기 위한 역할을 한다. 그러나 Training error보다는 "한번도 보지 못한 데이터"에 대한 성능이 더 중요하다. 즉 train/test error의 격차를 줄이는 것이 더 중요하다.

Model Ensembles

train/test error의 격차를 줄이는 가장 빠르고 쉬운 길은 바로 모델 앙상블이다. 모델 앙상블은 n개의 모델을 독립적으로 학습시키고 n개 모델 결과의 평균을 이용한다. 모델의 수가 늘어날수록 overfitting 줄어들고 성능이 조금씩(2%정도) 향상된다. ImageNet 같은 대회에서는 모델의 성능을 최대화시키기 위해 앙상블 기법을 사용하기도 한다.

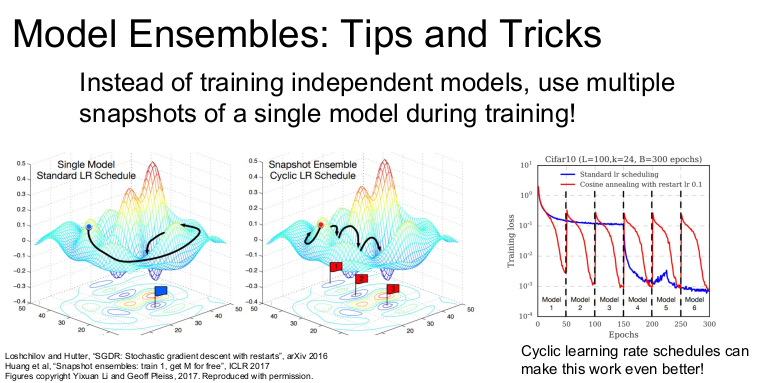
더 창의적인 방법으로는 학습 도중 중간 모델들을 저장(snapshots)하여 앙상블로 사용하고, Test time에는 여러 snapshots에서 나온 예측값들을 평균을 내서 사용하는 방법이 있다. 이런 앙상블 기법은 모델을 한 번만 Train시켜도 좋은 성능을 얻을 수 있게 한다.

Q. 모델간의 Loss 차이가 크면 한쪽이 overfiting일 수 있으니 별로 안좋고, 또 차이가 작아도 안 좋을 것 같다. 그러므로 좋은 앙상블 결과를 위해서 모델 간의 최적의 갭을 찾는 것이 중요하지 않을까?
중요한 것은 validation set의 성능을 최대화시키는 것이다. 따라서 우선 loss gap을 신경쓰지 않고 모델을 조금 더 Overfitting 시킬 수 있다면 좋은 성능을 낼 수 있을 것이다. validation set 성능과 이 갭 사이에는 묘한 관계가 있지만 Validation set 성능만 신경쓰면 된다.

Q. 앙상블 모델마다 하이퍼파라미터를 동일하게 정하는가?
다르게 정할 수도 있다. 다양한 "모델 사이즈", "learning rate", 그리고 "다양한 regularization 기법" 등을 앙상블할 수 있다.

또 다른 방법으로는 Polyak averaging이 있다. 학습하는 동안에 파라미터의 exponentially decaying average를 계속 계산한다. 이 방법은 학습중인 네트워크의 smooth ensemble 효과를 얻을 수 있다. checkpoints에서의 파라미터를 그대로 쓰지 않고 smoothly decaying average를 사용하는 방법이다. (?) 때로 성능이 조금 향상할 수 있다. 시도해볼만한 방법이나 자주 사용하지 않는다.

그러나 앙상블을 한다면 test time에 n개의 모델을 돌려야 할 수도 있으므로 좋은 방법이 아니다. (비용이 비싸므로 잘 사용하지 않는다.)

Regularization

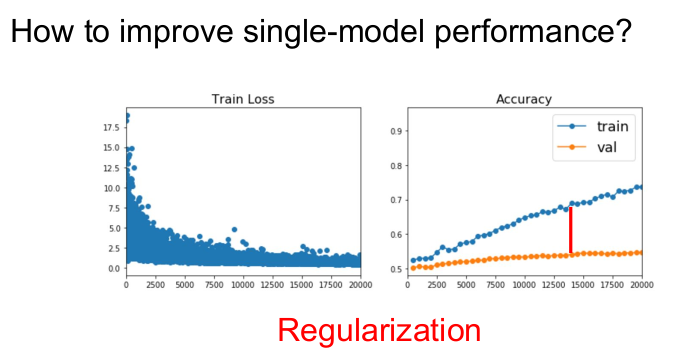
단일 모델로 성능을 향상시킬 수 있는 방법은 Regulaization이다. 3강에서 배웠듯 Regulaization은 모델이 training data에 overfit하는 것을 방지하고, 처음 본 데이터에서의 성능을 향상시킨다.

3강에서는 기존의 loss function에 regularization term을 더해주는 방법을 사용하였다. 그 때는 L2 regularization이 일반적으로 사용된다고 하였다. 그러나 L2 regularization는 Neural Network에서는 잘 사용하지 않는다. NN에서 자주 사용하는 regularization은 dropout이다.

Regularization: Dropout

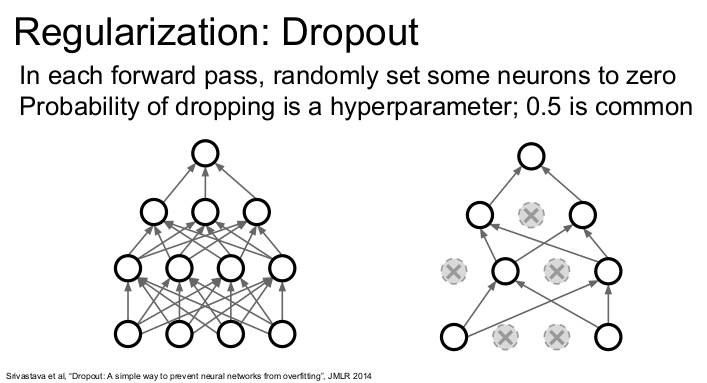
dropout은 forward pass 과정에서 임의로 일부 뉴런을 0으로 만든다. dropout은 먼저 한 레이어의 출력을 전부 구하고 일부의 뉴런(activation)을 0으로 만든 후 다음 레이어로 넘어간다. dropout은 forward pass iteration마다 모양이 계속 바뀐다. 위의 오른쪽 그림이 dropout이 적용된 것이다. 기본값은 p=0.5이다.

dropout은 FC layer에서 흔히 사용되지만 conv layers에서도 사용된다. activaton map에서 dropout을 시행하고, 일부 채널을 dropout할 수도 있다.

forward pass에서 dropout의 규현은 임의로 0으로 설정하는 2줄(H1, H2)이면 할 수 있다.

dropout은 일부의 activation 값을 0으로 만들어 training time의 네트워크를 훼손시키는데, 성능이 좋아지는 이유는 뭘까? 그 이유는 dropout이 특징들 간 상호작용을 방지하기 때문이다. dropout을 적용하면 네트워크가 일부의 features에만 의존하지 못하게 하고, 다양한 features를 고루 이용할 수 있게 한다. 따라서 dropout은 overfitting을 어느 정도 막아준다.

dropout에 대한 다른 해석도 있다. 왼쪽의 dropout을 적용한 네트워크는 뉴런의 일부만 사용하는 서브네트워크임을 알 수 있다. dropout으로 만들 수 있는 서브네트워크의 경우의 수는 다양하다. 따라서 dropout은 파라미터를 공유하는 서브네트워크 앙상블을 동시에 학습시키는 것이라고 할 수 있다. 즉 dropout은 거대한 앙상블 모델을 동시에 학습시키는 것과 같다. 그러나 뉴런의 수가 많아질수록 앙상블 가능한 서브네트웤크의 수가 기하급수적으로 늘어나므로 모든 서브네트워크를 사용할 수는 없다.

dropout을 test time에 사용하면 어떻게 될까? dropout을 사용하면 Neural network의 동작이 변한다. 기존 NN은 가중치 w와 입력 x에 대한 함수(f)이다. dropout을 사용하면 NN에 "random dropout mask"라는 임의의 입력 z가 추가된다. test time에는 임의의 값을 넣는 것은 좋지 않다. 예를 들어 분류하는 문제에서 결과가 매번 다르게 나온다면 좋지 않기 때문이다. 따라서 test time에서는 임의성을 적분을 통해 average out시킨다. (?) 이 적분을 다루는 것은 상당히 어렵기 때문에 이 문제를 해결하기 위해 z를 여러 번 샘플링해서 average out하여 적분을 근사시키는 방법도 사용한다. 하지만 이 방법도 test time에서 임의성을 없애지는 못한다.

dropout에서는 이 문제를 쉽게 해결할 수 있는 방법이 있다. 출력이 a, 입력이 x, y, 가중치 $w_1, w_2$ 인 뉴런이 하나 있다고 하자. 그러면 test time에서의 a의 기댓값은 $E(a)=w_1x+w_2y$ 이다. 이 네트워크에 dropout(p=0.5)를 사용하여 학습할 것이다. train time에서의 a의 기댓값은 다음과 같이 계산할 수 있다. dropout mask에는 4가지 경우의 수 $((w_1, w_2), (w_1, 0), (0, w_2), (0, 0))$ 가 존재하고, 그 값을 4개의 마스크에 대해 평균화시킨다.

train time에서의 a의 기댓값: $E(a) =\frac{1}{4}(w_1x+w_2y) + \frac{1}{4}(w_1x+0y) + \frac{1}{4}(0x+w_2y) + \frac{1}{4}(0x+0y) = \frac{1}{2}(w_1x+w_2y)$

train time의 기댓값은 test time의 기댓값의 반이다. 따라서 이 둘의 기댓값을 같게 하기 위해 네트워크 출력에 dropout probability(p=0.5)를 곱한다. 이 방법은 이전의 복잡한 적분식을 쉽게 근사화할 수 있는 방법이다.

많은 사람들이 Dropout을 사용할 때 test time에 모든 뉴런에 dropout probability을 곱하는 방법을 많이 사용한다.

정리하면 Forward pass에서는 Dropout을 추가하기 위해 일부 노드를 무작위로 0으로 만들어준다(코드 2줄). 그리고 test time에 dropout probability(p)를 네트워크 출력에 곱해준다.

Dropout을 역으로 계산하는 방법이 더 효율적이다. (inverted dropout) test time에는 계산 효율이 중요하므로 연산을 하나 추가하는 것은 좋지 않다. 따라서 test time에는 기존의 연산을 그대로 사용하고 대신 trian time에서 p를 나눠준다.

Q. dropout을 사용하면 Train time에서 gradient에는 어떤 일이 일어날까?
Dropout이 0으로 만들지 않은 노드에서만 Backpropagation이 발생하고, 각 스텝마다 업데이트되는 파라미터의 수가 줄어든다. 따라서 dropout을 사용하면 전체 학습시간이 늘어나지만 (?) 모델이 수렴한 후에는 더 좋은 일반화 능력을 얻을 수 있다.

dropout은 일반적인 regularization의 한 예이다. regularization의 패턴은 1) train time에는 네트워크에 임의성을 추가해 training data에 overfit하지 않게 한다. 2) Test time에서는 임의성을 평균화(근사화)시켜서 일반화한다.

Batch normalization도 regularization과 비슷한 동작을 한다. Train time에서 BN은 하나의 데이터를 mini batch로 샘플링하여 매번 서로 다른 데이터들과 만나게 한다. 샘플링된 데이터에 대해서 이 데이터를 얼마나 어떻게 정규화시킬 것인지에 대한 활률성(stochasticity)을 주었다(γ, β). 반면 test time에서는 정규화를 전체 데이터 단위로 수행함으로써 확률성을 평균화시킨다. 이런 특성은 BN이 regularization의 역할을 할 수 있게 한다. 따라서 BN을 사용할 때는 Dropout을 사용하지 않는다.

하지만 Dropout은 자유롭게 조절할 수 있는 파라미터 p가 있기 때문에 여전히 유용하다.

Regularization: Data Augmentation

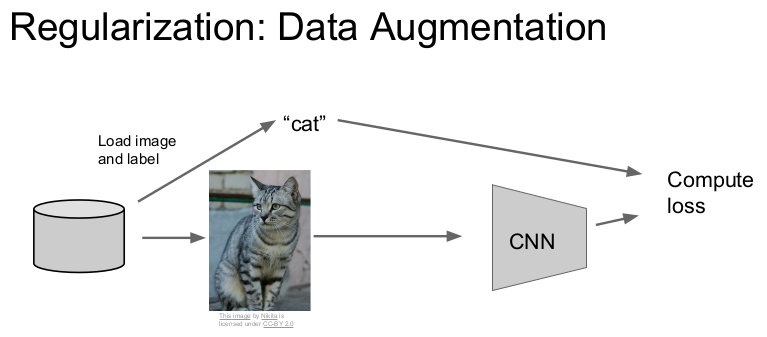
Regularization의 다른 예는 data augmentation가 있다. 기본적인 학습과정에서는 데이터와 레이블이 있고 이를 통해 loss를 계산해 매 스텝마다 CNN을 업데이트한다.

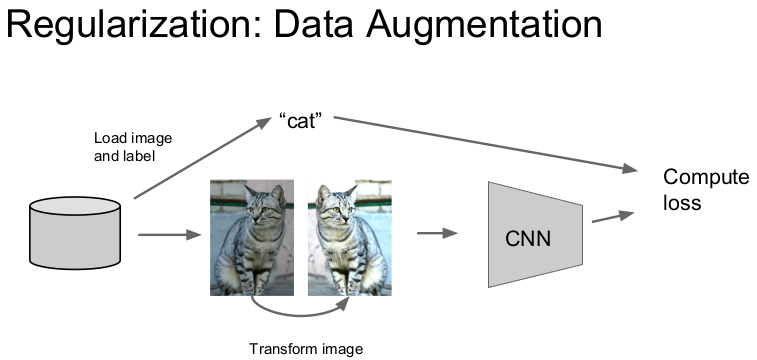
그러나 data augmentation에서는 train time에 이미지를 무작위로 변환시켜서 학습한다.

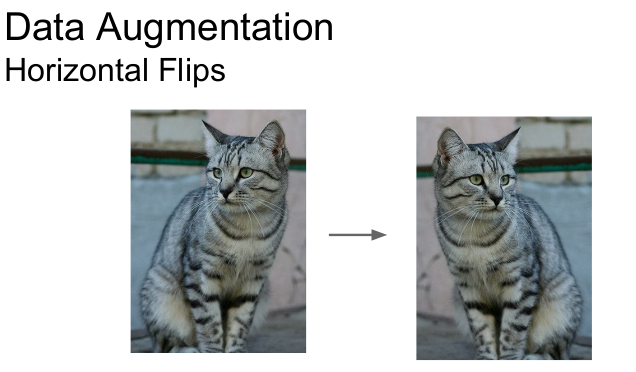
이미지를 세로축을 기준으로 하여 회전시킬 수 있다. (회전시켜도 고양이이다.)

이미지를 임의의 사이즈로 잘라서(crop) 사용할 수도 있다. test time에서는 "4개의 각 코너"와 "중앙"에서 잘라낸 이미지와 이들의 "반전 이미지"를 평균화시킨다. ImageNet 관련 모델들의 논문에서는 저자들이 하나의 이미지를 그대로 사용했을 때의 성능과 이미지 한장에서 10개를 잘라낸 결과의 성능을 비교하기도 한다. (10개 = (4개코너 + 중앙) x (원래 + 반전))

또 다른 방법으로는 학습 시 이미지의 contrast와 brightness를 바꾸는 color jittering도 있다. 더 복잡한 방법으로는 PCA의 방향대로 이미지를 샘플링하여 color offset을 학습 이미지에 더하는 방법이 있다. 이 방법은 color jittering을 좀 더 data-dependent하게 사용하는 방법이지만 자주 사용하는 방법은 아니다.

Regularization: 다른 방법

일반적으로 data augmentation는 어떤 문제에도 적용할 수 있는 "일반적인 방법" 이다. 어떤 문제를 풀 때, 이미지의 label을 바꾸지 않으면서 이미지를 변환시킬 수 있는 많은 방법들을 생각할 수 있다.

Train time에 입력 데이터에 임의의 변환을 시켜주게 되면 일종의 regularization 효과를 얻을 수 있다. 그 이유는 train time에는 확률성(stochasticity)이 추가되고 test time에는 평균화되기 때문이다. 지금까지 dropout, Batch Normalization, Data Augmentation를 살펴보았다. 이 외에도 다른 방법들도 있다. Regularization의 패턴을 잘 숙지하고 논문을 읽다보면 다른 방법들을 발견할 수 있을 것이다.

Dropout과 유사한 방법인 DropConnect이 있다. DropConnect은 weight matrix를 임의로 0으로 만들어준다. Dropout과 동작이 비슷하다.

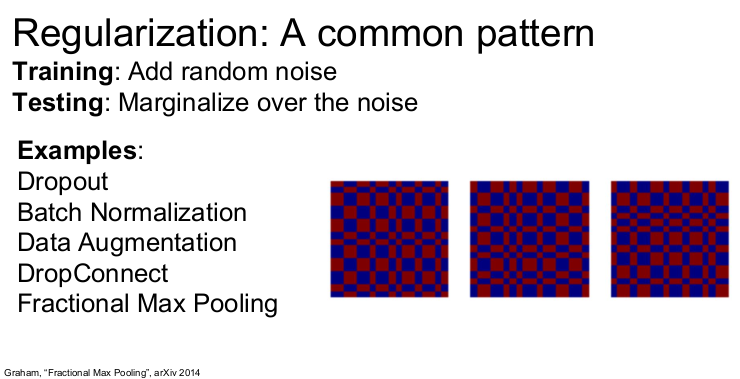
다른 한가지 방법은 Fractional Max Pooling이다. 자주 쓰지는 않지만 좋은 아이디어이다. 보통 2x2 maxpooling 연산은 고정된 2x2 지역에서 수행지만 fractional max pooling에서는 pooling 연산할 지역이 임의로 선정된다. 오른쪽 그림에서 Train time에 샘플링될 수 있는 임의의 pooling region을 볼 수 있다. test time에 stochasticity를 평균화시키려면 pooling regions를 고정시키거나 여러 개의 pooling regions을 만들고 평균화시킨다.

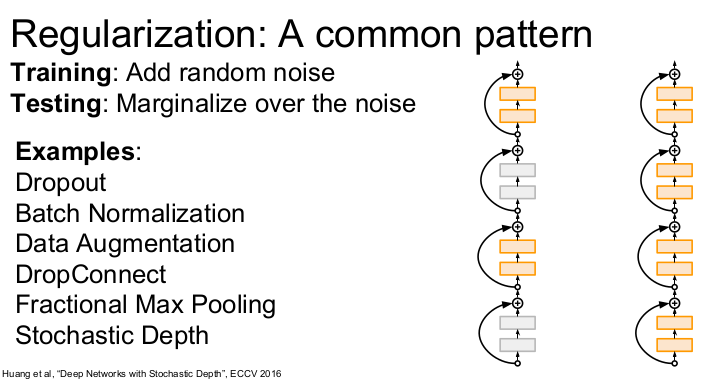
마지막으로 소개할 regularization 방법은 Stochastic Depth이다. 아주 깊은 네트워크가 있다고 하자. train time에 네크워크의 레이어를 임의로 제거하고, 일부만 사용해 학습한다. test time에는 전체 네트워크를 다 사용한다. (중요한 방법)

Q. 보통 하나 이상의 regularization 방법을 사용하는가?
일반적으로는 대부분의 네트워크에서 보통 잘 동작하는 batch normalization를 많이 사용한다. 보통 BN만으로 충분하지만 overfitting이 발생하면 다른 방법을 추가할 수 있다.

Transfer Learning

충분한 데이터가 없을 때, 학습이 overfitting할 수 있다. 이 문제를 해결할 수 있는 방법 중 하나가 Transfer learning 이다. Transfer learning은 적은 데이터로도 모델을 빠르게 학습시킬 수 있다.

Transfer learng은 기존에 학습된 모델을 가지고 와서 마지막 레이어만 초기화시켜 작은 데이터를 학습시킴으로써 모델이 잘 동작하게 만든다. 즉 ImageNet과 같이 큰 데이터셋을 CNN 모델로 학습시켜 학습된 features를 가져와 우리가 가진 작은 데이터셋에 적용한다. 만약 우리가 가진 문제가 C개(예: 10개)의 클래스로 분류하는 것이라면 기존 모델의 나머지 layers의 가중치는 고정시키고 CNN 모델의 가장 마지막 층인 FC Layer(최종 feature와 class scores 연결)만 초기화 시켜 ImageNet 학습 때 사용했던 (4096 x 1000)차원의 행렬을 (4096 x 10)행렬로 바꿔준다. 이 과정은 linear classifier를 학습시키는 것과 같다.

만약 데이터가 조금 더 있다면 네트워크의 더 많은 부분을 학습/업데이트 시킬 수 있다. 이 과정이 네트워크 fine_tuning 이다. 최종 레이어들을 학습시키고 난 후 전체 네트워크를 학습시킬 수도 있다. 데이터가 많을수록 네트워크의 더 많은 부분을 학습시킬 수 있다.

그러나 기존 Learning rate보다는 낮춰서 학습해야 한다. 그 이유는 기존의 가중치들이 이미 ImageNet으로 학습되어 있기 때문에 잘 동작하기 때문이다. 따라서 우리가 가진 데이터셋의 성능을 높이려면 이미 학습된 가중치를 조금씩만 수정하면 된다.

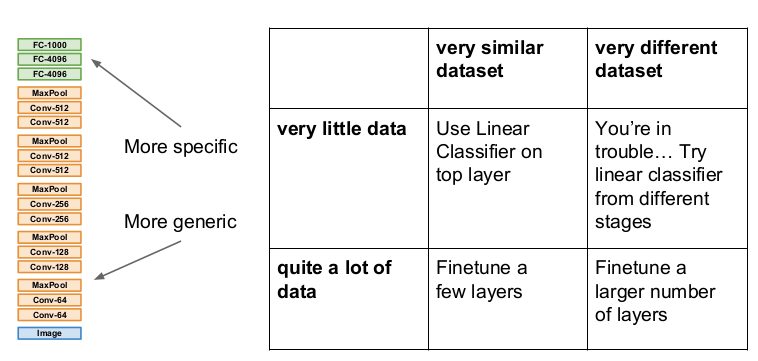
Transfer Learning에서는 위와 같이 4가지 사례를 살펴볼 수 있다. ImageNet과 비슷한 아주 작은 양의 데이터셋이 있다면 기존 모델의 마지막 레이어인 FC layer만 학습하는 Linear classifier를 사용한다. 데이터가 조금 더 많다면 모델 전체를 fine-tuning할 수 있다.

그러나 ImageNet과 다르게 생긴 데이터(예: 의료 영상 데이터)라면 다른 방법을 생각해야 한다. 만약 데이터셋이 크다면 더 많은 레이어를 fine-tuning함으로써 해결할 수도 있다. (아닐 수도 있다.)

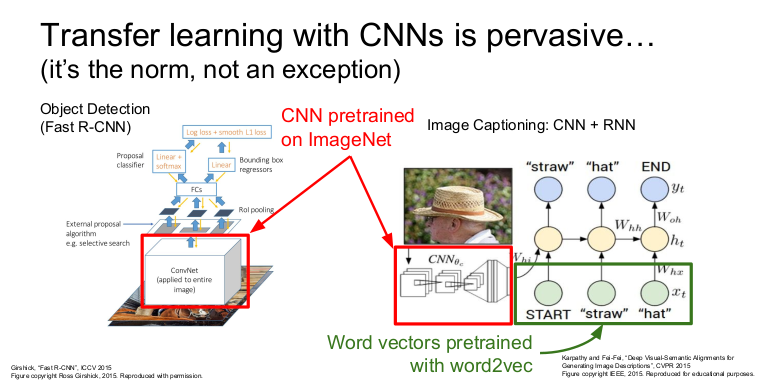
Transfer learning은 표준이 되었다. 왼쪽 그림은 Object Detection이고 오른쪽 그림은 Image Captioning의 시스템 다이어그램이다. 두 모델 모두 CNN모델을 가지고 이미지를 처리한다. 대부분의 이미지 처리는 ImageNet pretrained model을 사용하고 각자의 문제에 맞게 fine-tuning한다. Image Captioning의 경우 word vectors를 pretrain된 word2vec을 사용하기도 한다.

만약 문제에 대한 데이터셋이 작다면 가지고 있는 문제와 유사한 데이터셋으로 미리 학습된 pretrained model을 다운로드하여 그 모델의 일부를 초기화시키고 네트워크를 fine-tuning하면 잘 동작할 것이다. 이런 경우는 일반적이므로 대부분의 딥러닝 소프트웨어 패키지들은 model zoo를 제공한다. 접속하여 다양한 모델의 pretrained 버전을 다운로드할 수 있다.