그래프(Graph)는 가장 널리 사용되는 자료구조 중 하나 이다. 그래프는 데이터 간의 관계를 나타내는데 사용되며, 복잡한 데이터를 직관적으로 이해할 수 있게 해준다.
그래프의 구조
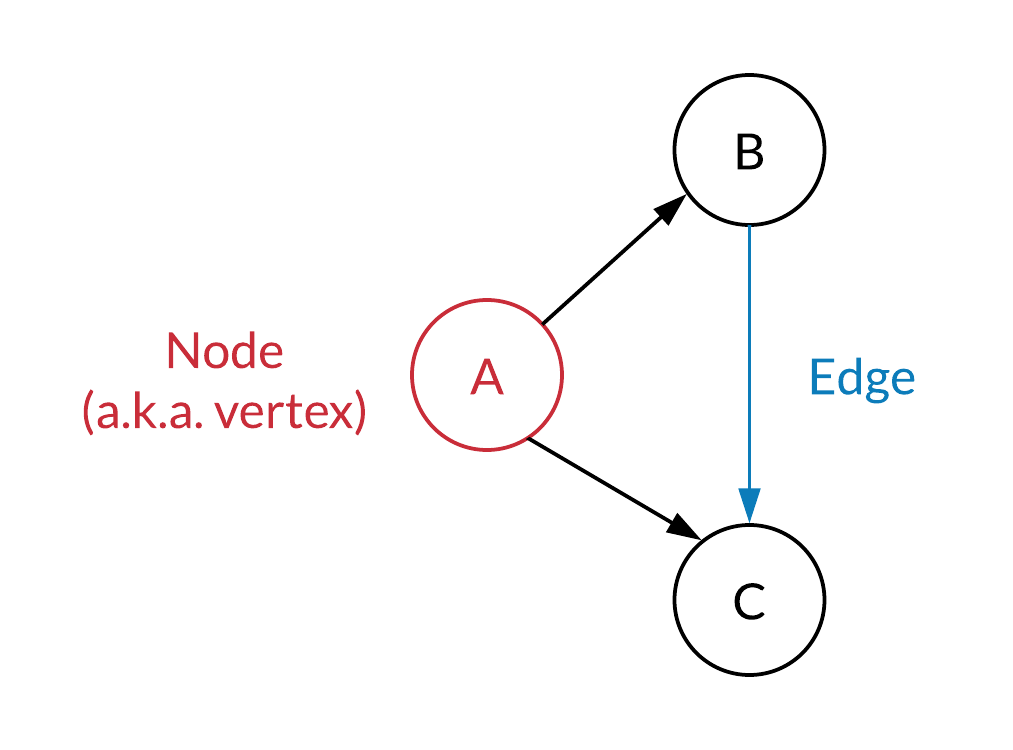
그래프는 보통 Node(노드)와 Edge(엣지)로 이루어져 있다.
Node(노드)는 데이터의 지점을 나타내며, Edge(엣지)는 노드 간의 관계를 나타낸다.
그래프 알고리즘의 종류
Directed vs unDirected
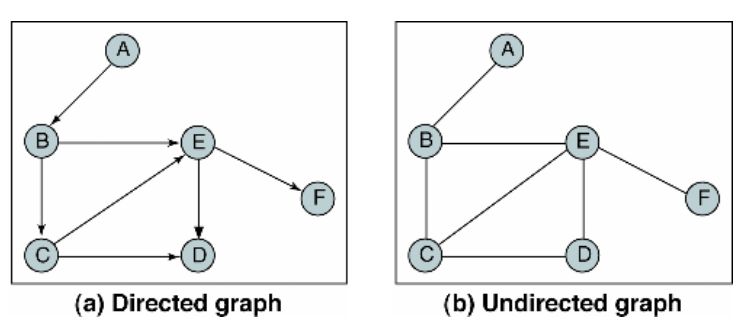
그래프는 방향성이 있을 수도 있고, 없을 수도 있다. 그래서 방향성이 있는 그래프를 directed graph라 불리며, 방향성이 없는 그래프를 undirected graph 로 불린다. 방향성 그래프에서 자기 자신을 가리키는 그래프도 있다. 그것을 self edge라 불린다.
Directed Graph
방향성 그래프에서도 여러가지 종류의 그래프로 나뉜다.
Acyclic graph vs Cyclic graph
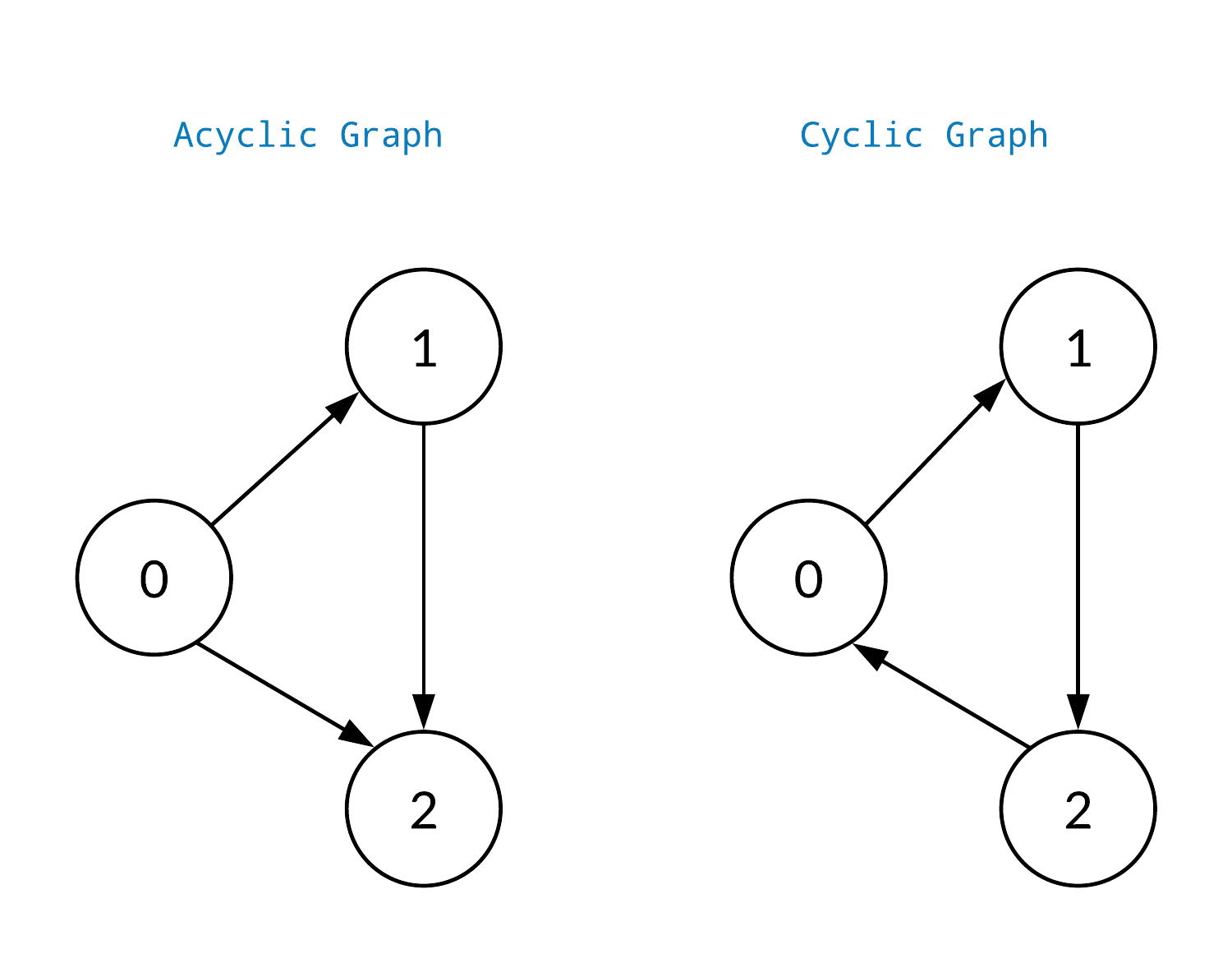
그래프 내부에 Cycle이 회전하는 것이 하나라도 있으면 cyclic graph 라 불리며, 없다면 acyclic graph 라 불린다.
Graph를 표현하는 방법
대개 그래프를 표현하는 방법은 3가지가 있다.
인접 행렬(Adjacency Matrix)
2차원 배열에다가 표현하는 방법
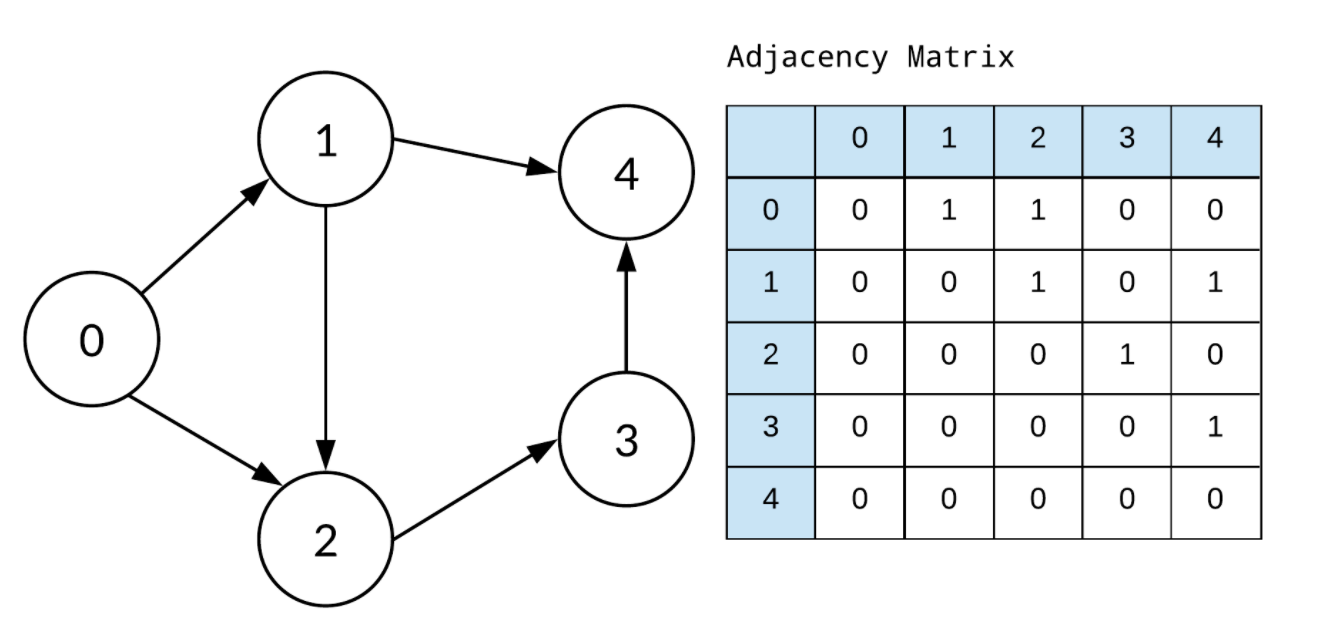
위 그림과 같이 표현할 수 있다. 하나의 예를 들어보자.
현재 0에서 1로 이동하는 노드는 가능하기 때문에 matrix[0][1] = 1 이다.
하지만 1에서 0으로 이동하는 노드는 불가능하기 때문에 matrix[1][0] = 0 이다.
이렇듯 2차원 배열로 이동이 가능한지 불가능 한지 표기하는 방법이다.
인접 리스트(Adjacency List)
배열에 노드들을 나열하고 Linked List로 표현하는 방법
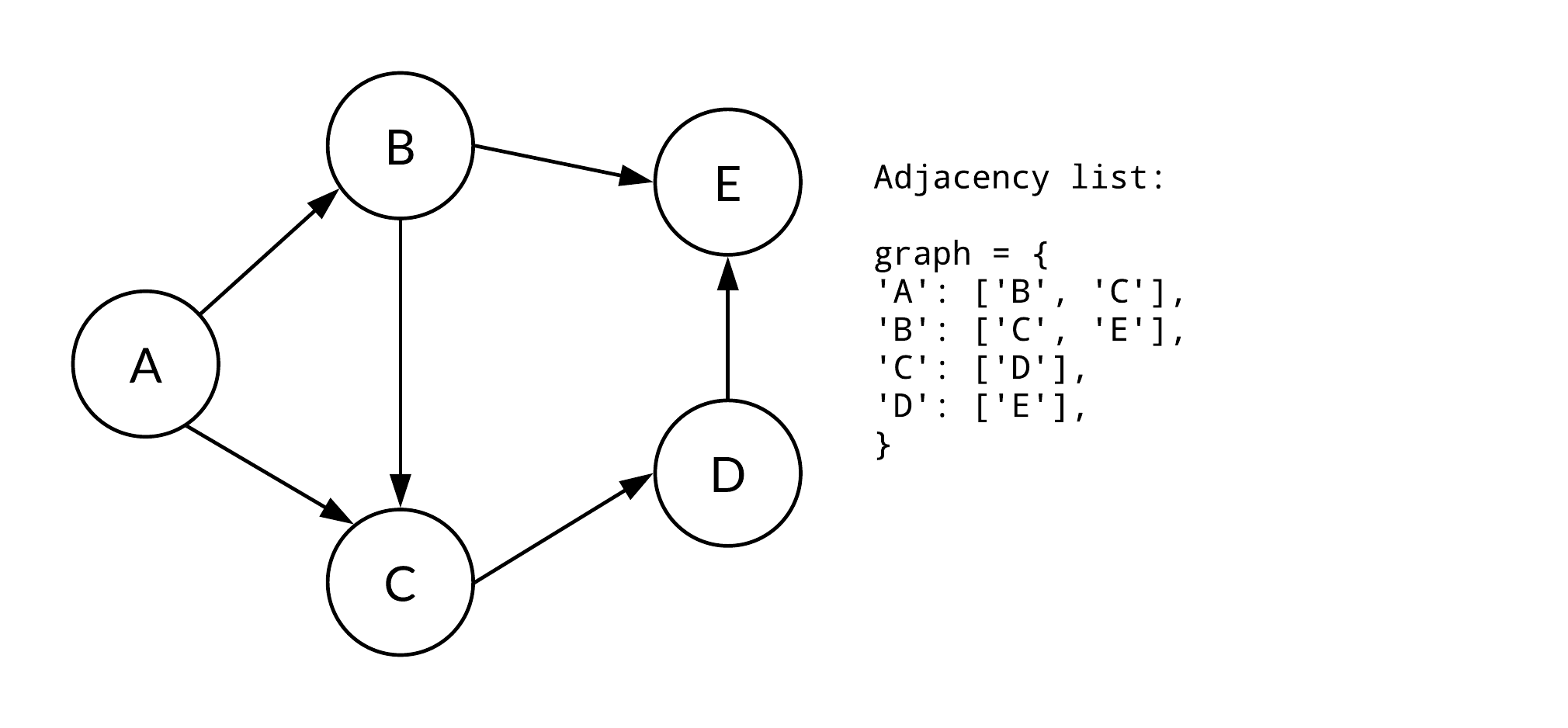
Adjacency List는 그래프를 표현하는 가장 흔한 방법 중 하나이다. 각 노드의
위 그림를 참고하여, 설명해보겠다.
노드 A에서 갈 수 있는 노드는 B와 C이다. 이것을 A라는 키값에 리스트를 저장하고 있으며, 리스트 내부에 B와 C를 저장 해놓는 것이다.
간선 집합(Edge sets/lists)
배열에 갈 수 있는 노드끼리 tuple로 묶어 저장하는 방법

Edge sets은 매우 간단한 그래프 표현 방법이다.
Graph 표현 방법에 대한 시간 복잡도
| 표현 방식 | 정점에 인접한 모든 간선 가져오기 | 전체 그래프 순회 | hasEdge(u, v) | 공간 |
|---|---|---|---|---|
| 인접 행렬 | O(V) | O(V2) | O(1) | O(V2) |
| 간선 집합 | O(E) | O(E) | O(E) | O(E) |
| 인접 리스트 | O(1) | O(V + E) | O(정점이 가지는 최대 간선 수) | O(E + V) |
