자료구조 알고리즘

코딩을 하다보면 sort를 여러번 사용해야하는 경우가 자주 발생한다. 특히 알고리즘을 풀다보면 시간초과(time out)가 되는 것을 종종 볼 수 있는데, sort 함수도 시간복잡도 계산에 포함되는 내용이기 때문에 신경을 써야하는 부분이다.그래서 sort의 대해서 알아

소수는 '1과 자기 자신 외의 약수를 가지지 않는 1보다 큰 자연수'입니다.2, 3, 5 이 세 가지 수의 경우를 보면2는 1과 23은 1과 35는 1과 5로 나누어집니다.이처럼 어떤 수를 나누었을 때 나머지가 0인 수를 그 수의 '약수' 라 합니다.위 숫자들은 1과

지구 둘레의 길이를 처음으로 계산했던고대 그리스의 학자 '에라토스테네스'그는 많은 수 중 소수를 찾아내는 방법을 생각해냈습니다.소수가 아닌 숫자를 하나씩 지워나가면서 구하는 방법이죠.모든 수의 약수인 1을 제외하고먼저, 소수 2를 제외한 2의 배수를 지웁니다.그리고 소

DP(Dynamic Programing)란?

이분 탐색(Binary Search)은 결정 문제(Decision Problem)의 답이 이분적일 때 사용할 수 있는 탐색 기법입니다. 이때 결정 문제란 답이 Yes or No인 문제를 의미하며 (이분 탐색 문제에서는) 보통 1개의 parameter를 가집니다.

GitHub: javascript 코드Heap Sort는 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법입니다. 내림차순 정렬을 위해서는 최소 힙을 구성하고 오름차순 정렬을 위해서는 최대 힙을 구성하면 됩니다. 만약 내림차순 정렬을 위한 최대 힙을 구현하려면

위 그림을 보면 좀 더 쉽게 이해할 수 있을 것 같다.퀵 정렬은 Pivot 이라는 선정된 기준값에서 작으면 왼쪽으로 모으고, 크면 오른쪽으로 모아서 Pivot을 기준으로 정렬을 시키는 방법이다. 그래서 1회 작업이 끝나면, Pivot의 위치는 고정이 된다.그래서 퀵 정

머지 정렬은 위 내용을 보면 쉽게 이해할 수 있을 것 같다.말 그대로 배열을 그룹화 하면서 모두 하나로 쪼갠 다음에 그룹별로 값을 비교하면서 하나의 배열로 합치면서 정렬이 진행되는 방식이다.위 그림의 과정 전체는 아래와 같다.그래서 합병 정렬의 시간 복잡도는 n개의 데

해시(Hash)는 데이터를 효율적으로 검색하기 위한 자료구조 중 하나입니다.해시는 데이터를 저장할 위치를 계산하는 데 사용하는 해시 함수와, 계산된 위치에 데이터를 저장하는 데 사용하는 배열로 이루어져 있습니다. 이렇게 함으로써 데이터를 빠르게 검색할 수 있습니다.해시

그래프(Graph)는 가장 널리 사용되는 자료구조 중 하나 이다. 그래프는 데이터 간의 관계를 나타내는데 사용되며, 복잡한 데이터를 직관적으로 이해할 수 있게 해준다.그래프는 보통 Node(노드)와 Edge(엣지)로 이루어져 있다. Node(노드)는 데이터의 지점을 나

전위탐색 vs 중위탐색 vs 후위탐색

그래프는 연결된 노드와 간선으로 이루어진 자료구조이다. 그래프는 다양한 분야에서 활용되며, 그래프를 탐색하는 알고리즘은 이러한 분야에서 중요한 역할을 한다.DFS는 깊이 우선 탐색 알고리즘으로, 스택이나 재귀 호출을 이용하여 구현할 수 있다. DFS는 시작 노드에서부터

스패닝 트리(Spanning Tree)는 그래프에서 모든 정점을 포함하면서 사이클이 존재하지 않는 부분 그래프이다. 그래프 내에서 가장 작은 비용을 가지는 간선을 선택하고, 이어진 정점을 그래프에서 제외하여 생성된다. 스패닝 트리는 그래프 내에서 여러 개를 가질 수 있

이진 탐색 트리(Binary Search Tree)는 노드들이 부모 노드보다 작은 값을 가지는 왼쪽 서브트리와 부모 노드보다 큰 값을 가지는 오른쪽 서브트리로 이루어진 트리이다. 이진 탐색 트리에서 탐색, 삽입, 삭제 연산은 모두 O(log n)의 시간복잡도를 가진다.

Dynamic Programming (DP)와 Depth-First Search (DFS)의 차이점은 무엇일까요? 문득 문제를 풀다보니, DP(동적프로그래밍)과 DFS(깊이우선탐색)이 뭐가 다른지 궁금해져서 조사해보면서 정리를 해보았다.우선 각자의 개념부터 먼저 알아보

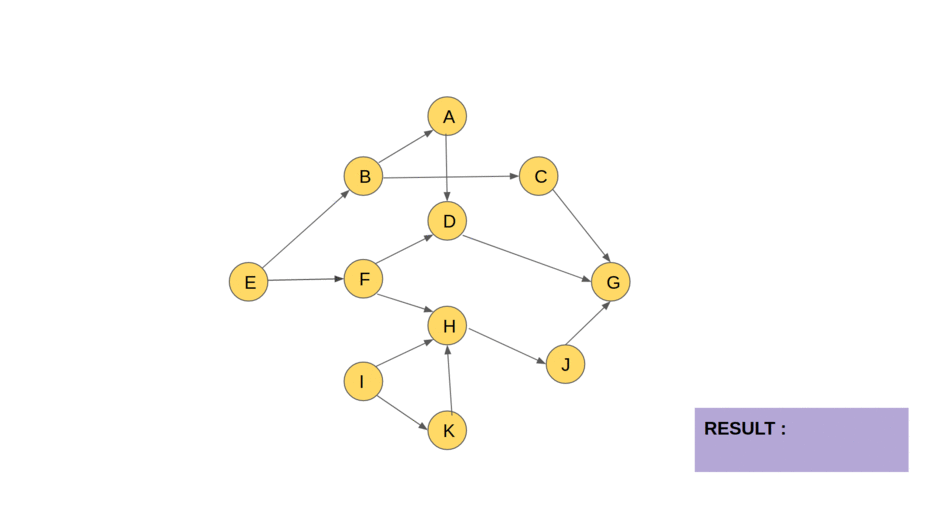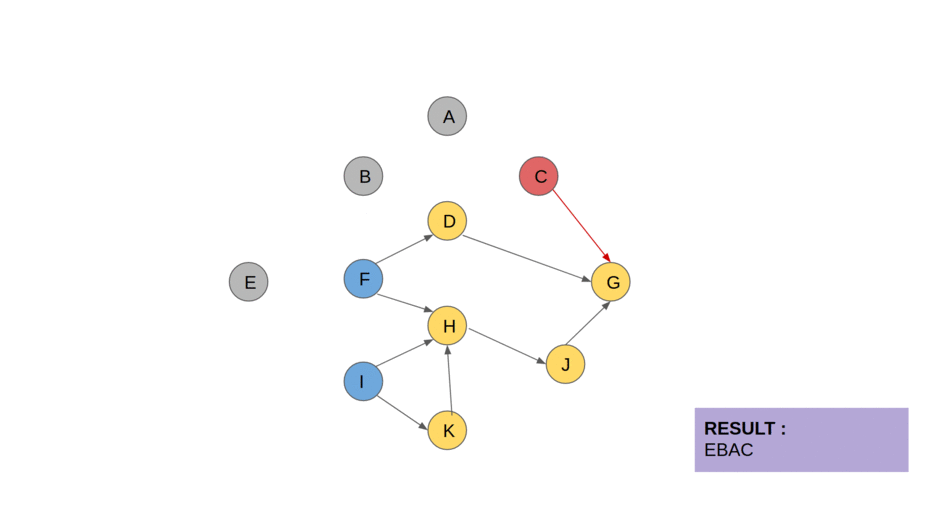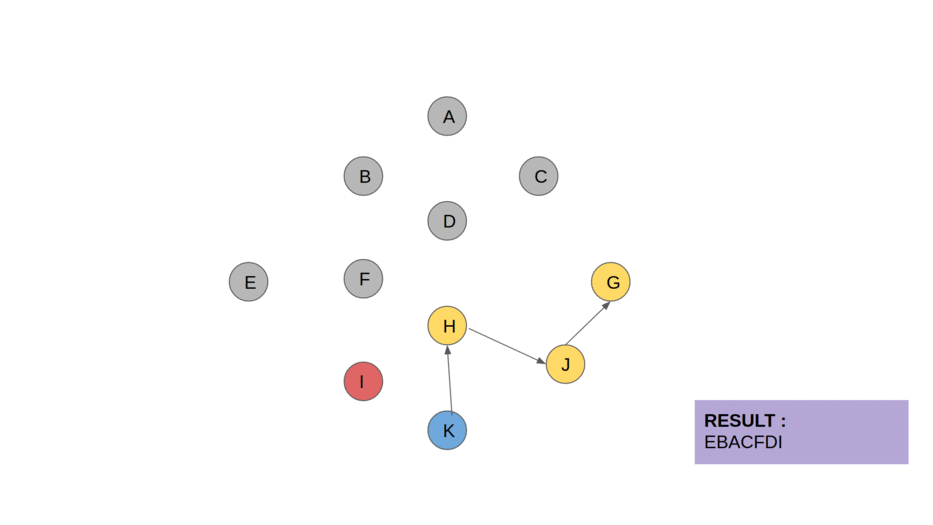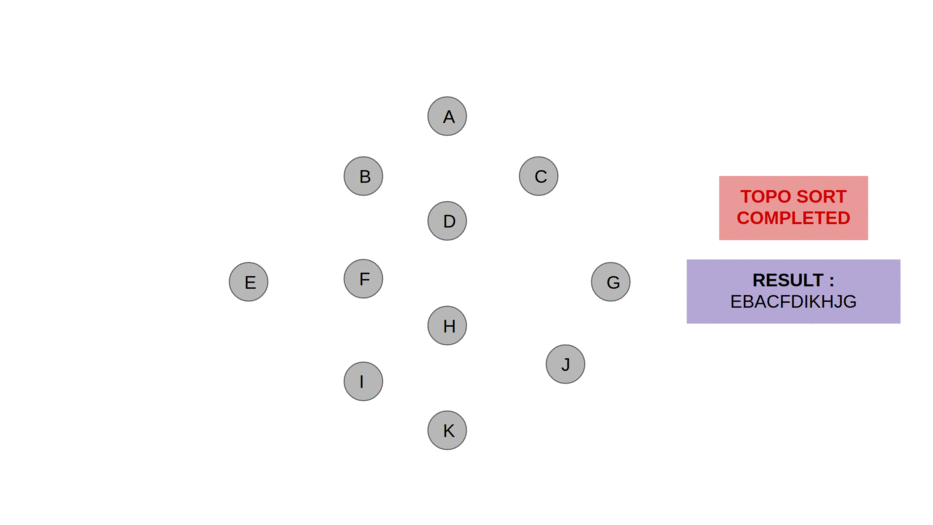
위상 정렬은 그래프 이론에서 사용되는 알고리즘으로, 각 노드들이 어떤 순서로 방문되어야 하는지를 결정하는 방법입니다. 이는 그래프에서 각 노드 간의 관계를 파악하고, 각 노드를 방문하는 순서를 결정할 때 사용됩니다.예를 들어, 일상적인 상황에서도 위상 정렬의 개념을 쉽