위상정렬이란?
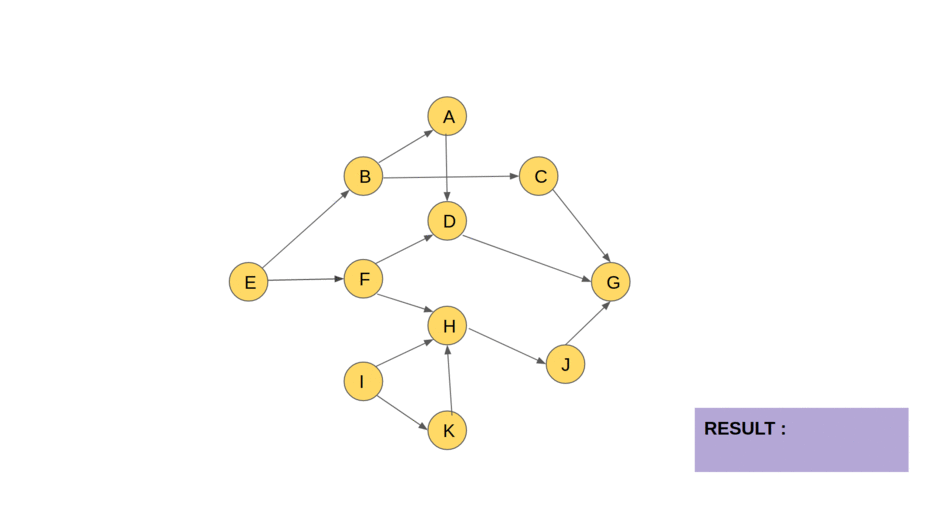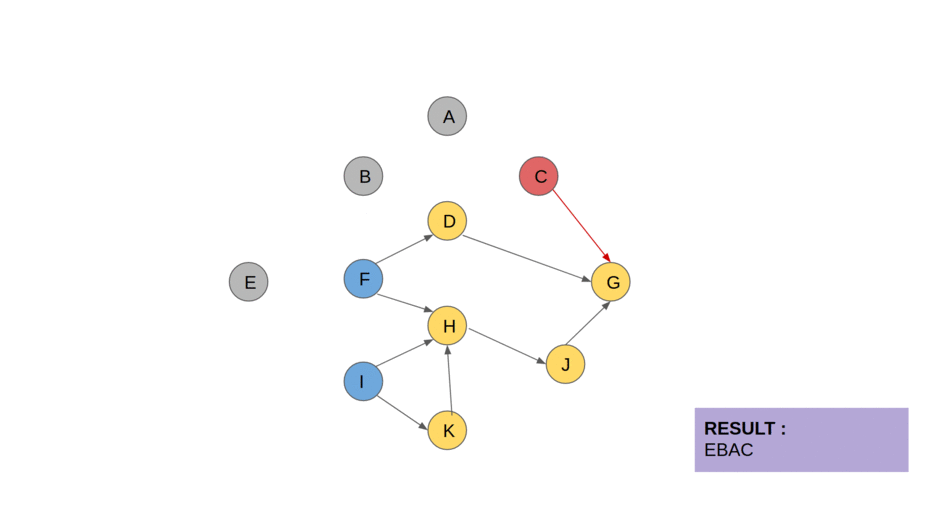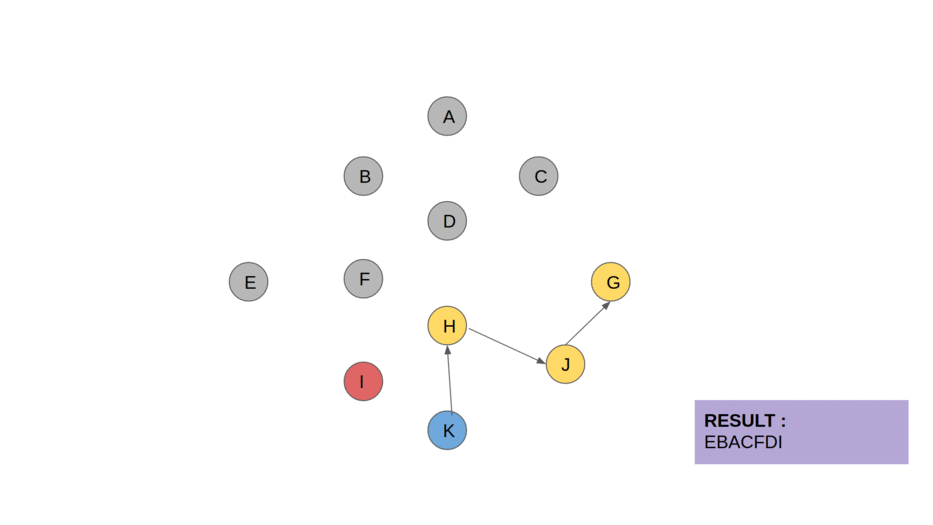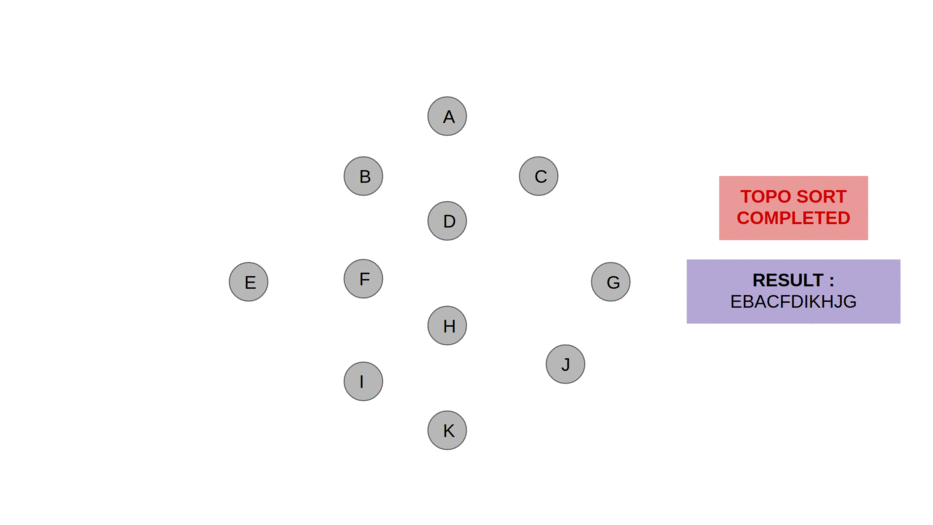
위상 정렬은 그래프 이론에서 사용되는 알고리즘으로, 각 노드들이 어떤 순서로 방문되어야 하는지를 결정하는 방법입니다. 이는 그래프에서 각 노드 간의 관계를 파악하고, 각 노드를 방문하는 순서를 결정할 때 사용됩니다.
예를 들어, 일상적인 상황에서도 위상 정렬의 개념을 쉽게 이해할 수 있습니다. 만약 여러분이 이번 주말에 청소를 하려고 한다면, 먼저 바닥 청소를 하고, 이어서 창문과 책상 등의 청소를 하게 될 것입니다. 즉, 바닥 청소라는 선행 작업이 완료되어야만, 이어지는 후행 작업들이 시작될 수 있습니다. 이때 바닥 청소와 창문 청소, 책상 청소 등을 각각 노드로 표현하고, 이들 간의 선행 관계를 간선으로 표현한 그래프를 생각해볼 수 있습니다.
위상 정렬은 이러한 그래프에서 각 노드를 정해진 순서대로 방문할 수 있는 순서를 찾아내는 알고리즘입니다. 이를 통해 어떤 작업을 수행할 때, 그 작업이 선행되어야 하는 작업들을 먼저 수행하는 순서를 알 수 있습니다.
예를 들어, 대학에서 수강 과목을 선택할 때, 선행 과목을 먼저 수강해야 하는 경우가 있습니다. 이때 위상 정렬을 이용하면, 선행 과목을 먼저 수강하고, 그 이후에 이어지는 수강과목을 결정할 수 있습니다.
위상 정렬 알고리즘은 다양한 방법으로 구현될 수 있습니다. 일반적으로는 DFS(Depth-First Search)나 BFS(Breadth-First Search)를 이용하여 구현합니다. 각 노드를 방문할 때마다 해당 노드와 연결된 간선들을 모두 탐색하면서, 선행 작업이 먼저 수행되어야 하는 노드들을 우선적으로 처리하게 됩니다.
이렇게 처리된 각 노드들은 위상 순서(topological order)라고 불리며, 위상 정렬 알고리즘을 통해 찾아낸 순서가 유효한 위상 순서인 경우, 모든 노드를 방문하는 일련의 작업을 수행할 때, 어떠한 충돌도 없이 작업을 마칠 수 있게 됩니다.
위상 정렬은 그래프 이론에서 중요한 개념 중 하나이며, 다양한 분야에서 활용됩니다. 예를 들어, 컴파일러에서 코드의 컴파일 순서를 결정하는 데 사용되기도 합니다. 또한, 프로젝트의 작업 일정을 수립하거나, 데이터 흐름을 분석하는 경우 등에도 활용됩니다.
코드 구현
파이썬에서 위상 정렬을 구현하기 위해서는 queue와 collections 라이브러리를 사용할 수 있습니다. 우선, 각 노드의 진입 차수(in-degree)를 구해야 합니다. 이후, 노드들을 진입 차수가 0인 것부터 큐에 넣습니다. 큐에서 노드를 꺼내면서 해당 노드와 연결된 간선들을 삭제하고, 진입 차수를 업데이트합니다. 이후, 진입 차수가 0이 된 노드들을 큐에 넣습니다. 큐가 빌 때까지 이 과정을 반복하면 위상 정렬 결과를 얻을 수 있습니다.
아래는 파이썬으로 위상 정렬을 구현한 예시 코드입니다.
from collections import deque
def topological_sort(graph):
# 각 노드의 진입 차수 계산
in_degree = [0] * len(graph)
for nodes in graph.values():
for node in nodes:
in_degree[node] += 1
# 진입 차수가 0인 노드들 큐에 삽입
q = deque()
for i in range(len(in_degree)):
if in_degree[i] == 0:
q.append(i)
# 정렬 결과 리스트
result = []
# 큐가 빌 때까지 반복
while q:
# 큐에서 노드 꺼내기
node = q.popleft()
result.append(node)
# 해당 노드와 연결된 간선 삭제 및 진입 차수 업데이트
for next_node in graph[node]:
in_degree[next_node] -= 1
if in_degree[next_node] == 0:
q.append(next_node)
# 사이클이 존재하는 경우
if len(result) != len(graph):
return []
return result
위 코드는 주어진 그래프를 딕셔너리 형태로 입력받아, 각 노드의 인접 리스트를 값으로 갖는 딕셔너리 graph를 생성합니다. in_degree 리스트는 각 노드의 진입 차수를 저장하며, 초기값은 0으로 설정됩니다. 이후, graph를 순회하면서 각 노드의 진입 차수를 계산합니다. 이어서, 진입 차수가 0인 노드들을 큐에 넣습니다. 큐에서 노드를 꺼내면서 해당 노드와 연결된 간선들을 삭제하고, 진입 차수를 업데이트합니다. 이후, 진입 차수가 0이 된 노드들을 큐에 넣습니다. 큐가 빌 때까지 이 과정을 반복하면 위상 정렬 결과를 얻을 수 있습니다.
