🔸이분탐색(Binary Search) 이란?

이분 탐색(Binary Search)은 결정 문제(Decision Problem)의 답이 이분적일 때 사용할 수 있는 탐색 기법입니다. 즉, 검색 범위를 줄여 나가면서 원하는 데이터를 검색하는 알고리즘이다.

선형 검색(Linear Search)의 경우에는 input 값을 하나하나 비교하면서 순서대로 찾아가는 방식이기 때문에, 인풋값이 길어지면 길어질 수록 시간이 증가한다.

그래서 이를 해결하기 위해서 나온 것이 이분탐색이다. 단, 이분탐색은 Sorted Array(정렬된 배열) 에서만 사용이 가능하다. 이분 탐색은 선형 탐색보다 엄청 빠른 속도로 값을 찾는다. 하지만 정렬된 배열이 필요하기 때문에 데이터 값을 추가하는데 오랜 시간이 걸리는게 특징이다.

🔸이분탐색vs선형탐색

종류	선형 탐색(Linear Search)	이분 탐색(Binary Search)
최고(Best)	O(1)	O(1)
최악(Worst)	O(n)	O(logN)

따라서, 데이터가 많고 검색이 많은 상황이라면, 이분탐색을 사용한다.
만약 데이터가 많지 않고, 데이터 추가되는 상황이 많다면, 선형탐색을 사용한다.

🔸이분탐색을 해보자

아래 그림과 함께 설명을 읽어보면 이해하기가 쉽다.

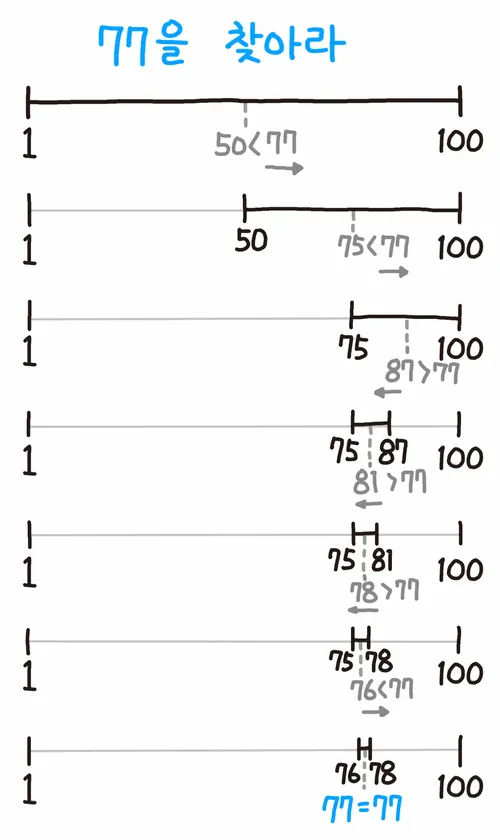
1. 정렬된 배열의 절반인 50부터 탐색을 시작한다.
2. 77은 50보다 크므로 왼쪽 포인터를 오른쪽으로 이동한다.
3. 다음은 75이며, 77은 75보다 크므로 마찬가지로 왼쪽 포인터를 오른쪽으로 이동한다.
4. 다음은 87이며, 77은 87보다는 작으므로 이번에는 오른쪽 포인터를 왼쪽으로 이동한다.
5. 이런 식으로 점점 범위를 좁혀 나가면 7번 이내에 무조건 숫자를 맞출 수 있게 된다.

🔸이분탐색을 사용할 때 주의해야할 점

1. lo, hi는 항상 정답의 범위를 나타낼 수 있도록 해야합니다. 예를 들어 lo를 출력해야 하는 문제의 답이 최대 n일 때 hi = n으로 선언하거나, hi를 출력해야 하는 문제의 답이 최소 0일 때 lo = 0으로 선언하면 안됩니다. (hi = n + 1, lo = -1로 선언해야 합니다)
2. 오버플로우에 주의해야 합니다. 이분 탐색을 사용하는 문제는 대부분 수의 범위가 크기 때문에 오버플로우가 발생할 수 있습니다.
3. 결정 문제의 정의에 맞게 Check함수를 잘 구현해야 합니다. 예를 들어 lower_bound는 v[i] >= k인 i의 최솟값을 구하는 함수이고, upper_bound는 v[i] > k인 i의 최솟값을 구하는 함수인데, Check 함수의 부등호를 조금만 틀려도 전혀 엉뚱한 값이 튀어나올 수 있습니다.

참고 문서

• 백준: 이분 탐색(Binary Search) 헷갈리지 않게 구현하기
• 나무위키: 이진탐색