이진 탐색 트리(Binary Search Tree)는 노드들이 부모 노드보다 작은 값을 가지는 왼쪽 서브트리와 부모 노드보다 큰 값을 가지는 오른쪽 서브트리로 이루어진 트리이다. 이진 탐색 트리에서 탐색, 삽입, 삭제 연산은 모두 O(log n)의 시간복잡도를 가진다.
이진 탐색 트리 구현하기

위 그림은 [21, 28, 14, 32, 25, 18, 11, 30, 19, 15]의 순서로 주어지는 값으로부터 이진 탐색 트리를 구축하는 과정을 보여준다. 맨 먼저 입력된 값이 뿌리(root) 노드가 되며, 그 다음부터는 입력값과 노드 간 대소관계에 따라 입력값의 노드 위치가 결정된다.
클래스 정의 및 초기화
자바스크립트로 이진 트리를 구현해 보았다.
우선 이진 탐색 트리를 구현하려면 먼저 그 재료가 되는 Node 클래스를 정의해야 한다. 그리고 Node 클래스는 노드의 값 value와 좌우 노드를 연결 시켜줄 left와 right 속성을 가진다.
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}이제 Node 클래스를 사용해 이진 탐색 트리 클래스인 BinarySearchTree를 구현해보자. 처음에는 비어 있는 트리이며, root에 null을 선언해준다.
class BinarySearchTree {
constructor() {
this.root = null;
}
}여기에 Node를 추가(insert()), 삭제(remove()), 탐색(search())할 수 있도록 메서드를 추가해야 한다.
추가 메서드 - insert()
BinarySearchTree에 insert() 메서드를 구현하여 트리에 새 원소를 추가할 수 있도록 해보자. 재귀를 사용하면 쉽다. 새로 추가할 원소의 값을 현재 노드의 값과 비교하여 왼쪽/오른쪽 중 알맞은 위치로 노드를 옮겨가며 삽입 위치를 체크한다.
// 새로운 node를 만든다.
insert(value) {
const newNode = new Node(value);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
// 대소관계를 비교하면서 트리의 빈 자리를 찾아 추가한다.
insertNode(node, newNode) {
if (node.value > newNode.value) {
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}탐색 메서드 - search()

원하는 값의 존재유무를 확인할 수 있도록 search() 메서드를 구현해보자. 이 역시 재귀와 값의 대소관계 비교를 통해 쉽게 구현할 수 있다.
search(value) {
return this.searchNode(this.root, value);
}
searchNode(node, value) {
if (node === null) {
return null;
}
if (node.value === value) {
return node.value;
}
if (node.value > value) {
return this.searchNode(node.left, value);
} else {
return this.searchNode(node.right, value);
}
}삭제 메서드 - remove()
삭제는 비교적 까다롭다. 왜 그럴까?
삭제할 노드의 자식이 없으면 문제가 없다. 자식이 하나인 경우엔 자식 노드를 삭제한 노드 위치로 가져오면 된다. 그러나, 삭제할 노드의 자식이 두개일 때는 어느 자식 노드를 어떻게 가져와야 할까?
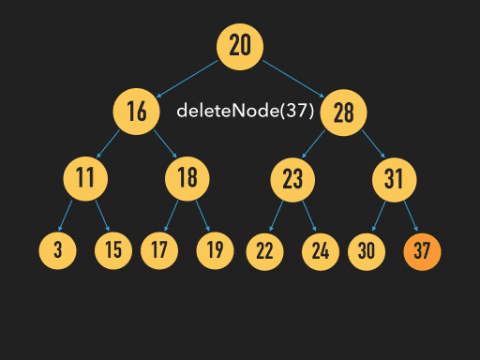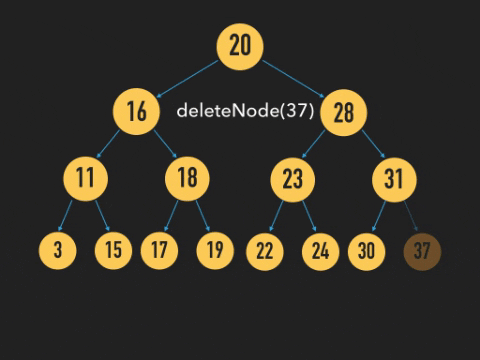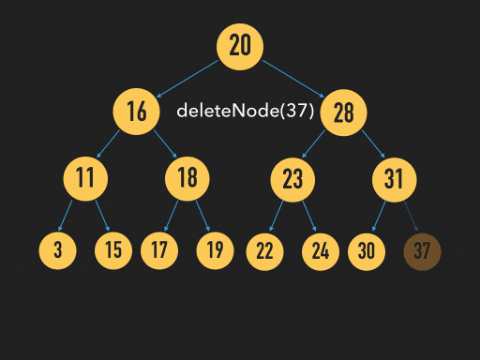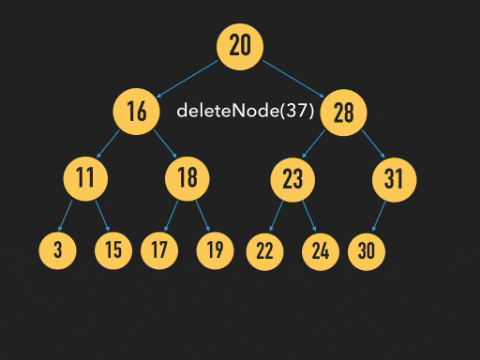
위와 같이 자식이 없는 Node의 경우에는 바로 삭제를 하면 된다.
하지만 자식이 있는 경우는 어떻게 해야 할까?
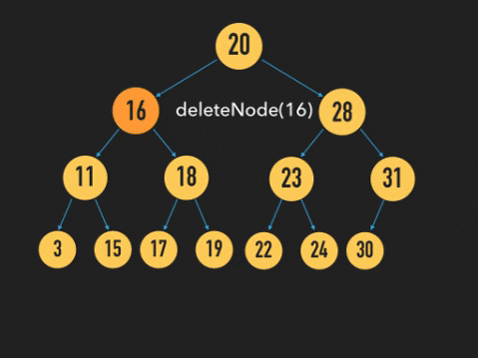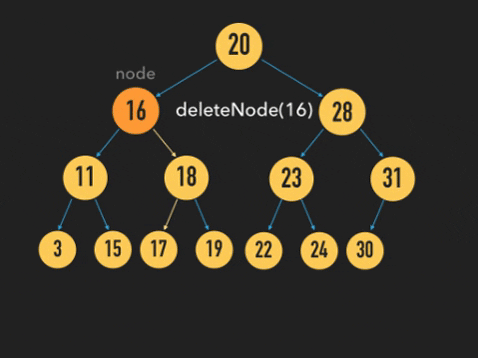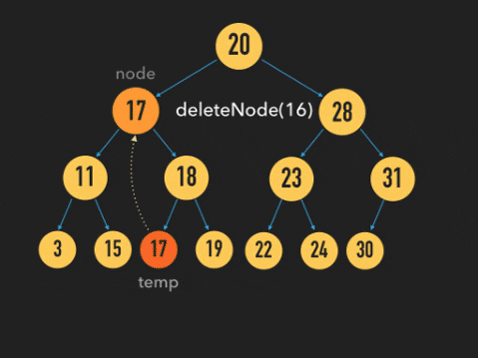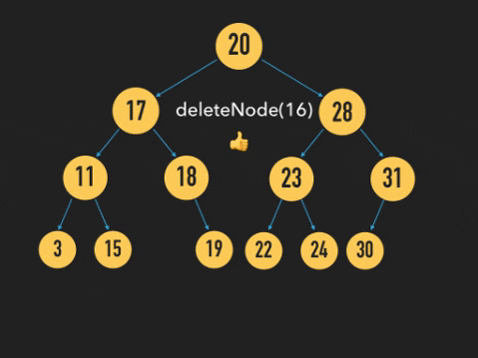
위 그림과 같이 삭제할 Node를 찾은 후, 삭제할 Node의 오른쪽 자식 Node에서 가장 왼쪽 Node 노드의 값을 삭제할 Node의 위치에 넣은 후, 노드를 삭제하는 방법을 사용했다.
remove(value) {
this.root = this.removeNode(this.root, value);
}
removeNode(node, value) {
if (node === null) {
return null;
}
if (node.value === value) {
if (
node.left === null &&
node.right === null
) {
return null;
}
if (node.left === null) {
return node.right;
}
if (node.right === null) {
return node.left;
}
const aux = this.findMinNode(node.right);
node.value = aux.value;
node.right = this.removeNode(
node.right,
aux.value,
);
return node;
}
if (node.value > value) {
node.left = this.removeNode(node.left, value);
return node;
} else {
node.right = this.removeNode(
node.right,
value,
);
return node;
}
}
findMinNode(node) {
if (node.left === null) {
return node;
}
return this.findMinNode(node.left);
}
아래 와 같이 노드를 삭제하는 방법이 더 있다.
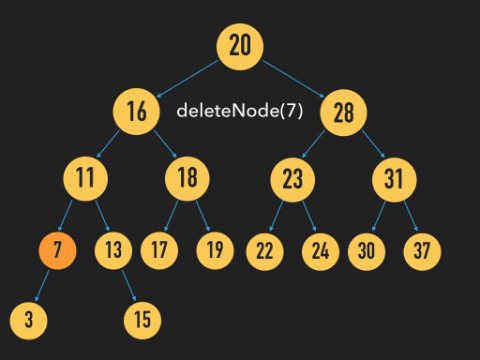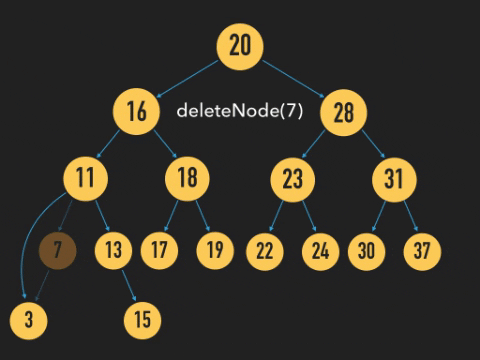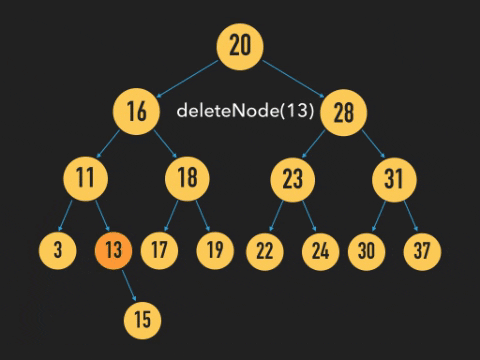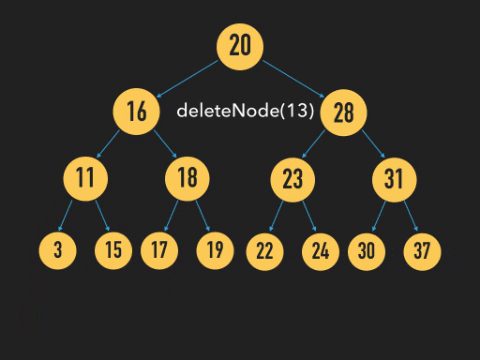
위 그림과 같이 아래 삭제할 Node의 root 노드와 자식 노드를 연결시켜주고 노드를 삭제시켜주면 된다.
전체코드
전체코드는 아래를 참고하시면 된다.
전체 코드 보기: [ GitHub ] BinarySearchTree
