Heap Sort ? 🤔
GitHub: javascript 코드

Heap Sort는 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법입니다. 내림차순 정렬을 위해서는 최소 힙을 구성하고 오름차순 정렬을 위해서는 최대 힙을 구성하면 됩니다. 만약 내림차순 정렬을 위한 최대 힙을 구현하려면 힙은 1차월 배열로 쉽게 구현될 수 있습니다.
Heap Sort는 2가지 단계로 이루어집니다. 첫 번째 단계에서는 최대 힙을 구성하는 과정이며, 두 번째 단계에서는 삭제 연산을 통해 힙에서 최대 값을 차례로 빼내어 정렬하는 과정입니다.
- 최대 힙을 구성합니다. 이를 위해 정렬할 요소들을 힙에 모두 삽입한 후, 힙의 루트 노드부터 시작하여 부모 노드와 자식 노드 중 더 큰 값이 있는 쪽으로 이동시키면서 힙을 구성합니다. 이 과정을 모든 노드에 대해 반복하면 최대 힙이 완성됩니다.
- 최대 값을 가지는 루트 노드를 삭제하고 루트 노드를 가장 마지막 노드와 교환합니다.
- 처음부터 끝까지 다시 최대 힙을 구성하고, 루트 노드를 삭제하고 교환하는 과정을 반복합니다.
- 이러한 과정을 반복하면서 정렬된 배열을 얻을 수 있습니다.
Heap Sort 장점
- in-place algorithm 과 merge sort는 보다 효율적이며, 추가적인 배열이 필요하지 않다.
- 항상 nlogn을 보장해준다.
- max 또는 min 값을 구할 때는 시간복잡도는 O(1)이다.
vs Quick Sort / vs Merge Sort
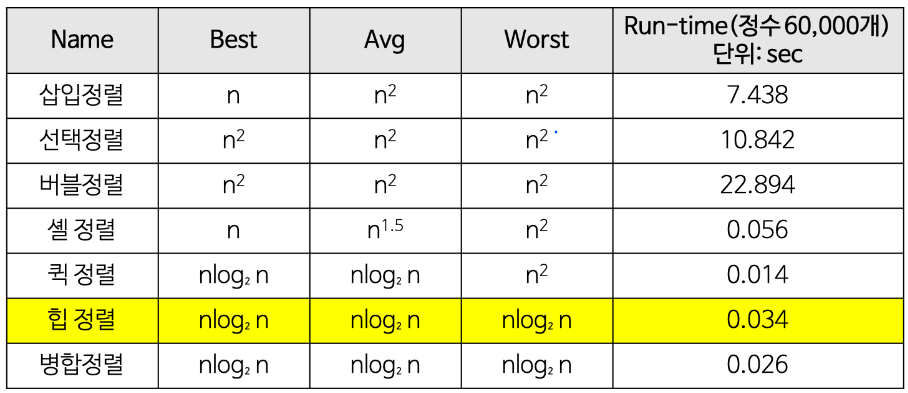
일반적인 속도만 비교하자면, Quick sort나 Merge Sort보다 느리다.
안정성을 보장하지 않는다. 즉, 같은 값에 대해서는 순서가 보존되지 않을 수 있다.
