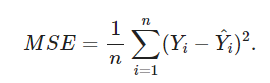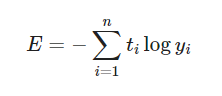1. 신경망의 구성
신경망이란?
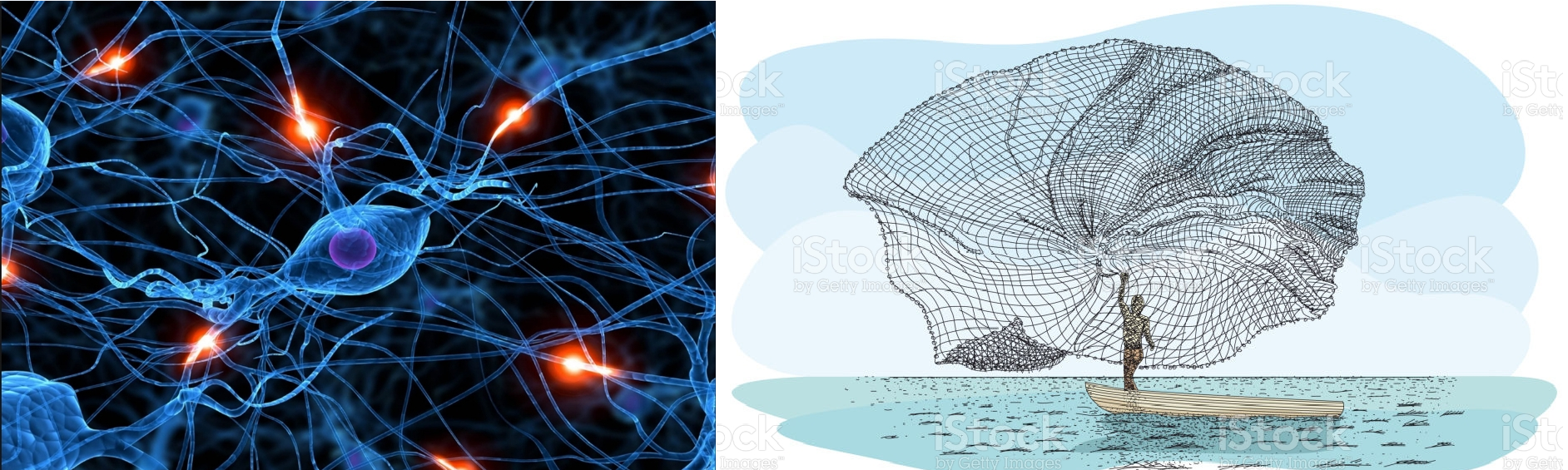
우리 뇌에는 1000억개에 가까운 신경계 뉴런들이 있고 이 뉴런들은 매우 복잡하게 얽혀 조금 물러서서 보면 하나의 거대한 그물망과 같은 형태를 이루고 있다. 이를 우리는 신경망이라고 부른다.
퍼셉트론(Perceptron)
그리고 머신러닝/딥러닝 과학자들은 이런한 뇌의 신경망 구조를 착안하여 퍼셉트론(Perceptron)이라는 형태를 제안하며 이를 연결한 형태를 인공신경망이라고 부르기 시작했다.
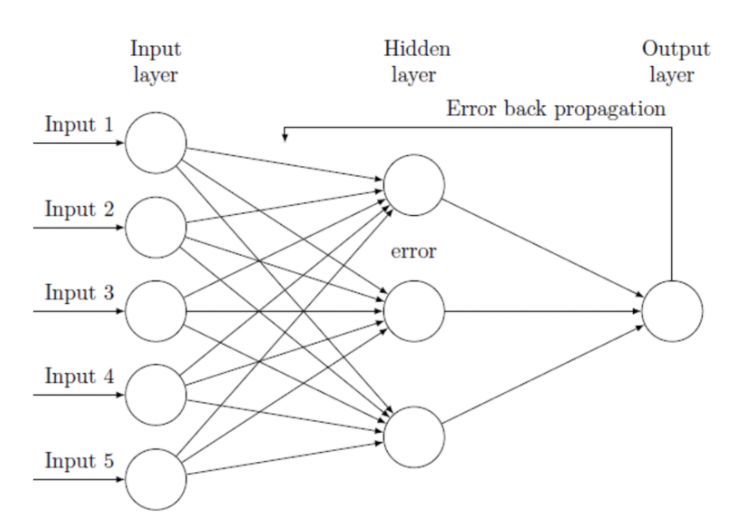
 (좌)퍼셉트론, (우)다중 퍼셉트론
(좌)퍼셉트론, (우)다중 퍼셉트론
다중 퍼셉트론에서 보이는 레이어를 살펴보면 입력층(input layer), 출력층(output layer)그리고 은닉층(hidden layer)가 있다. 보통 입력층과 출력층 사이에 있는 모든 층을 은닉층이라고 부르고 인공신경망을 표현할 때에는 노드를 기준으로 레이어를 표시해서 3개의 레이어라고 생각 할 수 있지만 실제로는 총 2개의 레이어를 가졌다.
💡 ( Tip ) 레이어 개수를 셀 때는 노드와 노드사이에 연결 부분이 몇 개인지 세면 쉽게 알 수 있다.
인공신경망을 구성하며 위의 다중 퍼셉트론처럼 은닉층이 많아지면 많아질수록 인공신경망이 "깊어졌다(DEEP)"라고 이야기하며 우리가 하려는 딥러닝은 충분히 깊은 인공신경망을 활용하며 이를 보통의 단어로 DNN(Deep Neural Network)라고 부른다.
파라미터(Parameters) / 가중치(Weights)
앞에서 설명한 입력층-은닉층, 은닉층-출력층 사이에는 사실 각각 행렬이 존재합니다.
그 행렬의 형태는 입력값이 100개, 은닉노드가 20개라면 "100x20"의 형태를 가진 형렬이 존재하고 여기에 출력값이 10개라면 은닉층-출력층 사이에는 "20x10"의 형태를 가진 행렬이 존재한다.
이 행렬들을 Parameter 혹은 Weight라고 부르며 인접한 레이어 사이에는 아래와 같은 관계가 성립한다.
2. 활성화 함수와 손실 함수
활성화 함수(Activation Functions)
다중 퍼셉트론의 또 다른 중요한 구성요소는 바로 활성화 함수인데 딥러닝에서 이 활성화 함수의 존재가 필수적이다.
간단하게 설명하자면 이 활성화 함수는 보통 비선형 함수를 사용하는데 이 비선형 함수를 다중 퍼셉트론 안에 포함시키면서 모델의 표현력을 좋아지게 만들어준다.
활성화 함수 1. Sigmoid
위와 같은 비선형 함수를 sigmoid라고 하며 파이썬으로 표현하면 아래와 같다.
def sigmoid(x): return 1 / (1 + np.exp(-x)) sig = sigmoid(a1) print(sig[0]) # sigmoid의 출력은 모든 값이 0에서 1사이에 있다.출력값
[0.71054984 0.52905551 0.46431738 0.51448048 0.64600668 0.67992026
0.8476983 0.40783071 0.3255252 0.6023858 0.46674095 0.55724645
0.87741522 0.72357138 0.61354501 0.4436175 0.78866167 0.34391609
0.63633906 0.4455516 0.33747163 0.73799929 0.60717187 0.59668883
0.41398438 0.60611891 0.64394084 0.2900367 0.64890973 0.4893765
0.08570879 0.53722463 0.48556319 0.74993183 0.41667574 0.54007566
0.33218701 0.22148587 0.56820075 0.4827034 0.24750372 0.28449555
0.28886275 0.34270077 0.32269618 0.24979073 0.41965474 0.60008566
0.79189452 0.53188799]
예전부터 많이 사용해 왔지만 현재에는 여러 문제점이 발생하여 ReLU 함수를 더 많이 사용한다.
💡 ( Tip ) sigmoid의 문제
- Vanishing gradient현상 발생
- exp함수 사용 시 비용이 커짐
활성화 함수 2.Tanh
tanh 함수는 함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결 했지만 여전히 Vanishing Gradient문제가 존재한다.
활성화 함수 3. ReLU(Rectified Linear Unit)
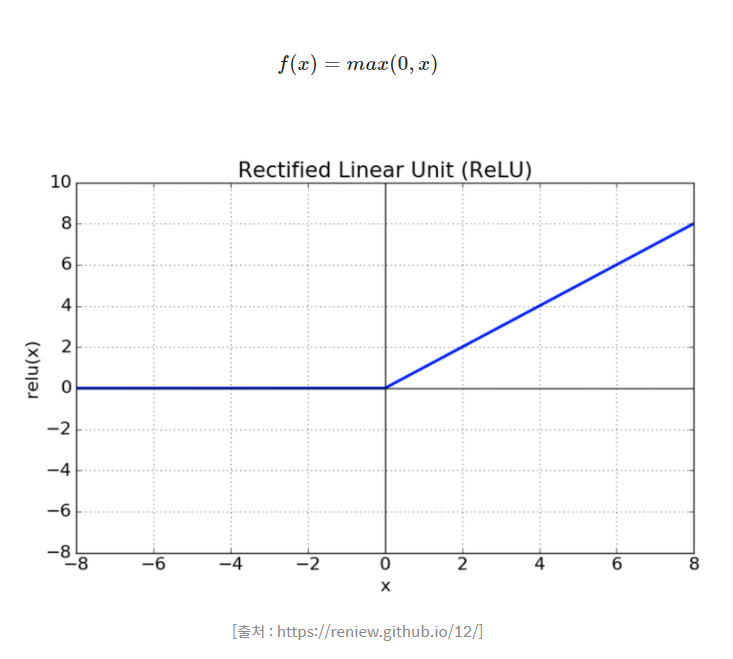 ReLU의 경우 sigmoid나 tanh함수에 비해 학습이 빠르고 exp()를 사용하지 않아 연산 비용이 크지 않고 구현이 매우 간단한 장점이 있다.
ReLU의 경우 sigmoid나 tanh함수에 비해 학습이 빠르고 exp()를 사용하지 않아 연산 비용이 크지 않고 구현이 매우 간단한 장점이 있다.
이 함수 또한 DeadReLU와 같은 몇몇 문제점이 있지만 그건 다음에 알아보자.
손실함수(Loss Functions)
이렇게 비선형 활성화 함수를 가진 여러 개의 은닉층을 거쳐 다음 신호 정보들은 출력층으로 전달 된다. 이때 우리가 원한느 정답과 전달된 신호 정보들 사이의 차이를 계산하고, 이 차이를 줄이기 위해 각 파라미터들을 조정하는 것이 딥러닝의 전체적인 학습 흐름이다.
이 차이를 구하는 데 사용되는 함수는 손실함수 또는 비용함수라고 부르며 대표적으로 평균제곱오차(MSE : Mean Square Error)와 교차 엔트로피(Cross Entropy)가 존제한다.
- 평균제곱오차
교차 엔트로피
더 자세한 내용을 알고 싶다면 --> 손실함수
3. 경사하강법
이제 앞에서 오차를 구했으니 우리는 그 오차를 줄여나가야 한다.
이 과정은 우리가 산 정상에 있다고 생각하고 빠르고 정확하게 내려가는 것을 목표로 하는 것과 유사하다.
이를 위해 경사하강법이 존재하고 아래의 사진과 같이 산에서 안전하게 내려오는 방법을 찾는 것처럼 각 단계의 기울기를 구해서 오차가 적은 방향으로 이동하는 것이 우리의 목표이다.
그러면 위의 사진 처럼 경사하강법을 사용하면 산 아래에 잘 도착할 수 있는가?
만약 보폭이 매우 큰 거인이라면 산 아래로 내려가지 못하고 골짜기에 빠지고 말 것이다.
여기서 우리는 학습률(Learning Rate)이라는 개념을 도입해 적절한 보폭으로 내딛으며 산을 내려가야 한다.
단, 보폭을 적절히 설정했다해도 출발점에 따라 하산하는 시간이 빨라지거나 느려질 수도 있다. 그것을 알기 위한 Parameter 값의 초기화를 참고해보자.
4. 오차역전파법(Backpropagation)
우리는 손실 함수를 통해 구해진 오차를 가지고 각 파라미터들을 조정하는 경사하강법에 대해 알게 되었다. 그러면 이 기울기를 어떻게 입력층까지 전달하며 파라미터들을 조정해 나갈 것인가?
이에대한 해답은 오차역전파법(Backpropagation)이다.
오차역전파법은 앞에서 설명한 다중 퍼셉트론을 학습시키기 위한 일반적인 알고리즘 중 하나이다. 이는 출력층의 결과와 내가 뽑고자 하는 타겟값과의 차이를 구한 뒤 그 오차값을 각 레이어들을 지나면서 역전파 해가며 노드가 가지고 있는 변수들을 갱신해 나가는 방식이다.