- 필요한 선수과정
확률, 확률변수, 조건부 확률 등등의 기본적인 확률론 개념이 필요하다.
아래의 링크는 베이즈 정리 설명 전 필요한 확률개념을 설명하며 전개해나간다. 참고해 공부하면 좋을 것 같다 :)
http://infoso.kr/?cat=35
- 베이즈 정리란?
사전확률(prior)과 우도(likelihood)를 이용해 사후확률(posterior)을 구하는 Thm이다.
이렇게 3가지 용어 사전확률, 우도, 사후확률이 등장하는데 식을 보며 이해해보자.
P(A|B) = =
(위의 식에서 분모의 P(B)가 시그마...로 변경되는 이유는 Joint Probability와 조건부확률 부분을 공부해보자.)
결론부터 말하면 사전확률(prior)는 P(A)이고 우도(likelihood)는 P(B|A)이고 사후확률(posterior)은 P(A|B)이다. 즉, 식을보면 우도와 사전확률로 사후확률을 구하는 것을 확인할 수 있다.
그래서, 우도와 사전확률을 가지고 사후확률을 구하는 것은 알겠으나 사후확률이 갖는 의미는 뭔데??
이는 베이즈정리의 대표적인 예시인 유방암 검사관련 문제를 보며 의미를 알아보자.
- 예제 1) 미국에서 정기적으로 건강 검진을 받는 40대 여성의 1%가 유방암을 가지고 있다. 유방암에 걸린 여성의 80%가 유방촬영검사(mammogram test)에서 양성 반응을 보였으며, 유방암을 걸리지 않은 여성 중 9.6%도 유방촬영검사에서 양성 반응을 나타냈다. 어떤 40대 여성이 정기 검진 때 유방촬영검사에서 양성 반응이 나왔다면 그녀가 실제로 유방암에 걸려 있을 확률은 얼마인가?
Sol)
두 확률변수 X, Y가 있다고하자.
X = 실제로 유방암에 걸렸는가
: 실제로 유방암이 발병
: 실제로 유방암이 발병하지 않았다.
Y = 유방촬영검사 결과
: Possitive
: Negative
문제에서 "40대 여성의 1%가 유방암을 가지고 있다."는
P(X = ) = 0.01 (당연히, P(X = ) = 0.99) 뜻한다.
문제에서 "유방암에 걸린 여성의 80%가 유방촬영검사(mammogram test)에서 양성 반응을 보였으며"는 P(Y = | X = ) = 0.8 (당연히, P(Y = | X = ) = 0.2) 뜻한다.
문제에서 "유방암을 걸리지 않은 여성 중 9.6%도 유방촬영검사에서 양성 반응을 나타냈다." P(Y = | X = ) = 0.096 (당연히, ~ ) 뜻한다.
문제에서 구하고 싶은 것은 "40대 여성이 정기 검진 때 유방촬영검사에서 양성 반응이 나왔다면 그녀가 실제로 유방암에 걸려 있을 확률은?"
즉, P( X = | Y = ) = =
을 구해야한다. 위에 문제에서 수치를 다 줬으니 대입만 해주면 끝난다.
P( X = | Y = ) = = 0.078이다.
- 베이즈정리를 두가지 관점으로 해석
-
두 조건부확률 (우도와 사후확률)의 관계성
: 사후확률 P(A|B)를 구하고 싶을 때 P(B|A)를 가지고 구할 수 있다. (이는 수학적으로 관계성의 측면에서 의미가 깊다고 생각한다.) -
사전확률과 추가적인 데이터(우도)를 가지고 의미있는 사후확률을 만든다.
: 이는 위의 문제에서 사전확률(P(X=))은 0.01이었다. 하지만, 사후확률(P( X = | Y = ))은 0.078이다. 추가적인 데이터를 사용해 0.01 -> 0.078로 끌어올렸다. (물론, 이 끌어올림이 쓰임에 따라 좋고 나쁨이 정해질 것이다.)내가 중요하게 생각하는 부분은 추가적인 데이터로 구제화된 의미를 찾아낼 수 있다는 부분이다. ( 구체화된 의미 : 유방암촬영검사의 결과가 양성으로 나왔는데도 그 사람이 실제로 유방암에 걸렸을 확률이 0.08밖에 되지 않는다. 여기서, 0.08인 이유는 유방암 발현 자체의 확률이 0.01이라 매우 작아서이다.)
- ML에서 베이즈 정리가 쓰이는 부분
검색을 해보니 ML에서 베이즈 정리는 Classification(분류)문제에 많이 응용된다. Naive Bayes Classifier, Gaussian Naive bayes classifier(GNB), Bayesian Networks들을 이용해 스팸필터, 텍스트분류, 추천시스템등 다양하게 이용된다.
1. Naive Bayes Classifier
Naive Bayes Classifier는 베이즈 정리를 기반인 통계적 분류기이다. 성능을 내기위해서는 2가지 조건이 있는데 모든 Feature들이 서로 독립이어야하고 데이터가 대용량으로 있어야한다. 그 이유는 아래의 분류기 작동방식을 살펴보면서 알아보자.
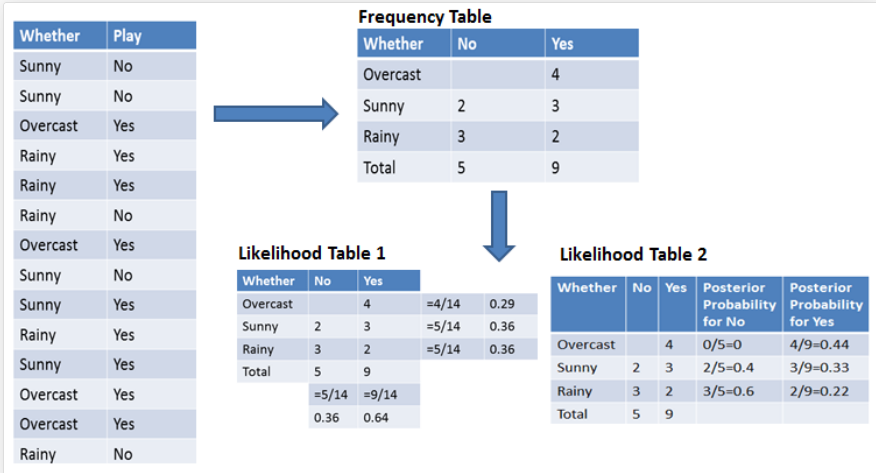
사진 출처: DataCamp
Q1. Overcast 날씨에 경기를 하는지 안하는지 분류해라!
즉, 우리가 구하고 싶은 것은 훈련데이터를 사용해 아래의 확률값을 구해
이때, Feature는 1개이다. (날씨가 흐린지 맑은지 등등)
-
P( Yes | Overcast ) =
-
P( No | Overcast ) =
더 높은 확률로 예측 Label을 주도록 기계를 학습시키면 된다.
Sol 1)
P( Overcast | Yes ) = 4/9 = 0.44 & P(Yes) = 9/14 = 0.64 & P(Overcast) = 4/14 = 0.29 이다. 이를 위의 식에 대입해 계산하면 P( Yes | Overcast ) = 0.98 이다. 즉, 흐린날씨에는 경기를 진행할 확률이 무려 0.98이나 되는 것이다.
Sol 2)
사전확률(Prior) P(Overcast) = 4/14 = 0.29, P(No) = 5/14 = 0.36이다. 우도(likelihood)는 P(Overcast|No) = 0/5 = 0 이다. 따라서, P( No | Overcast ) = 0 이다.
Now, Naive Bayes Classifier은 새로운 Overcast데이터가 입력되면 Play를 한다고 분류해 Predict Label을 출력할 것이다.
보통 데이터는 Feature의 특징이 여러 개이다. 이때는 어떻게 구하는지 살펴보자.
Q2. 날씨가 overcast, 기온이 Mild일 때 경기를 하는지 않하는지 분류해라.
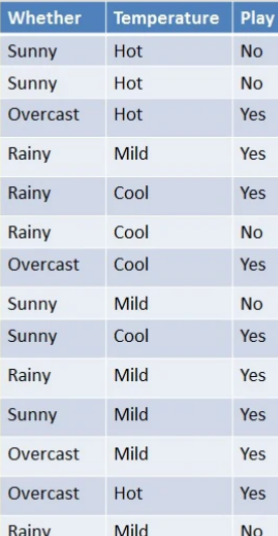
사진출처: DataCamp
위의 문제와 비슷하게 아래의 확률을 구해 비교하면 된다.
-
P( Yes | Overcast, Mild ) =
-
P( No | Overcast, Mild ) =
이때, Feature들이 서로 독립이어야하는 이유가 중요하다.
Sol 1)
사전확률
: P(Overcast, Mild) = P(Overcast) P(Mild) (독립이라서) = (4/14) * (6/14) = 0.1224
( 위의 식이 변하는게 궁금한 분들은 Joint Probability의 Overcast, Milde확률변수가 서로 Independent 할때 특성을 공부해보자! )
우도
: P(Weather=Overcast, Temp=Mild | Play=Yes) = P(Overcast|Yes) P(Mild|Yes)이다. 각각을 구해보면 P(Overcast|Yes) = 4/9 = 0.44, P(Mild|Yes) = 4/9 = 0.44이므로 최종값은 0.44 * 0.44 = 0.1936 이다.
이제 베이즈 정리에 대입하면 = 0.1936 * 0.64 / 0.1224 = 1이다. 따라서, 분류기는 Sol 2)를 구해서 하면되는 Sol 1)의 값을 이길 수 없으니 Play 한다고 Predict한다.
이렇게, Naive Bayes Classifier의 Feature들의 독립성이 중요한 이유를 문제를 풀면서 이해해보았다.
이제 데이터의 대용량일때 좋은 성능을 낸다고 했는데 한 가지 가정을 해보자. 관측 기간을 일주일이라고 하고 관측한 날중 날씨 Feature가 Sunny한 Sample이 한 개 있고 그 Label이 Play값이 No이면 분류기는 무조건 예측값을 No라고 한다. 이는, 의미있는 분류를 하지 못하는 것이다. 따라서, 데이터양이 많으면 많을 수록 정확한 분류를 한다. (근데, 이건 모든 ML Model에 해당할 것 같다 :) )
시간이 날때 코드로 Naive Bayes Classifier를 구현해야겠다! (2023 01 10)
2. Gaussian Naive bayes classifier(GNB)
위의 Naive bayes classifier 방식에서 likelihood를 구할 때 Feature(즉, 확률변수)가 정규분포를 따르는 개념을 기반으로 사후확률을 구하는 것이다.
쉽게 이야기 하자면 Whether ~ 를 따른다는 것이다.
(https://datascienceschool.net/02%20mathematics/08.04%20%EC%A0%95%EA%B7%9C%EB%B6%84%ED%8F%AC%EC%99%80%20%EC%A4%91%EC%8B%AC%EA%B7%B9%ED%95%9C%EC%A0%95%EB%A6%AC.html)
정규분포를 사용해 likelihood를 구해보자.
Whether = Overcast | Play = Yes가 평균 와 표준편차 를 가지는 정규분포를 따른다고 하자. 그러면, P(Overcast|Yes)를 구할때 정규분포의 pdf를 사용해 값을 구할 수 있다. ( pdf = 이다.)
위의 pdf의 x값에 Whether = Overcast | Play = Yes의 확률변수의 값을 넣어주면 P(Overcast|Yes)값을 구할 수 있다.
즉, Gaussian Naive bayes classifier은 Naive bayes classifier의 likelihood를 구하는 과정 빼고는 분류하는 방식 및 계산이 다 똑같다.
3. Bayesian Networks
베이지안 네트워크는 Feature의 인과 관계를 그래프로 나타내고 분석하는 확률모형이다. 딥러닝의 성능이 월등히 올라가기전에 주목을 받았던 모델로 확률 변수의 분포를 학습하는 확률 그래프 모형(Probabilistic Graphical Model, PGM)이다.
Graph는 노드(Node)와 엣지(Edge)나타낸다. 베이지안 네트워크에서의 노드는 데이터의 Feature가 되고, 엣지는 확률적인 관계가 됩니다.
아래의 예시를 통해 베이지안 네트워크를 만들어보자.
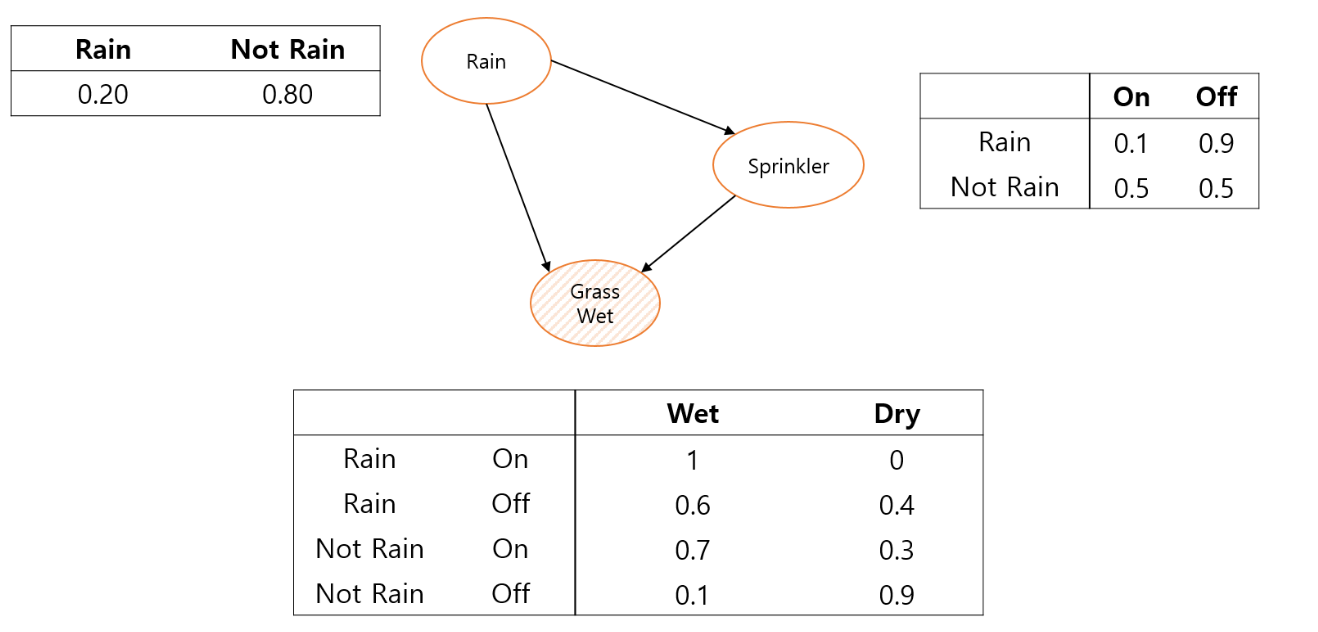
사진출처: tmax_ai
여기서, Grass Wet은 2개의 edge를 받고 있다. 즉, P(Grass Wet | Rain, Sprinkler)
로 Grass Wet은 Rain과 Sprinkler Feature에 영향을 받는 것임을 알 수 있다.
Sprinkler는 1개의 edge를 받고있다. 즉, P(Sprinkler | Rain)로 Rain Feature의 영향을 받는 것을 알 수 있다.
이처럼 베이지안 네트워크는 우리가 관심 있는 확률 변수들 간의 상관 관계 혹은 인과 관계를 그래프로 나타내고, 주어진 데이터를 통해 확률 분포를 계산하여 원하는 질문에 대답을 찾는 모델입니다.
