문제

https://programmers.co.kr/learn/courses/30/lessons/42898

계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.

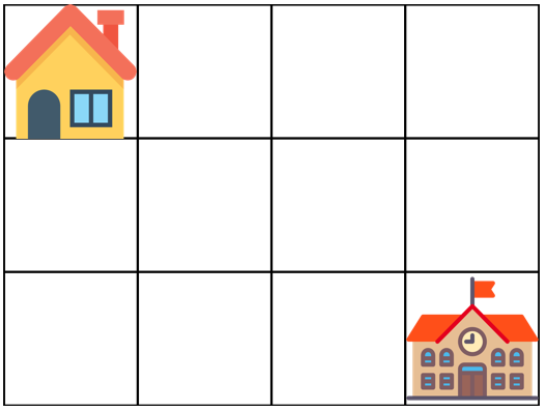
아래 그림은 m = 4, n = 3 인 경우입니다.

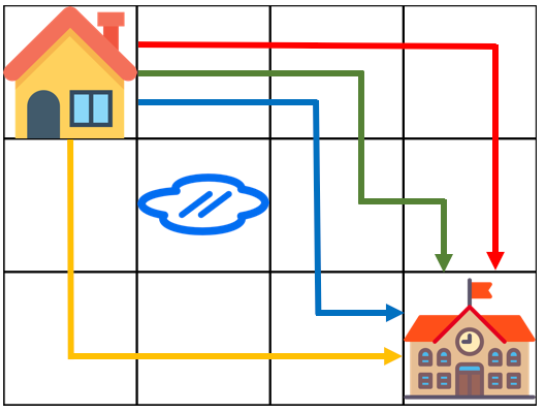
가장 왼쪽 위, 즉 집이 있는 곳의 좌표는 (1, 1)로 나타내고 가장 오른쪽 아래, 즉 학교가 있는 곳의 좌표는 (m, n)으로 나타냅니다.

격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.

제한 사항

• 격자의 크기 m, n은 1 이상 100 이하인 자연수입니다.
• m과 n이 모두 1인 경우는 입력으로 주어지지 않습니다.
• 물에 잠긴 지역은 0개 이상 10개 이하입니다.
• 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않습니다.

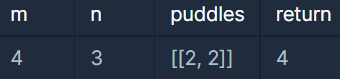
입출력 예시

• 위의 입력의 결과는 아래와 같다.
  

아이디어

👎 문제를 잘못 읽어서 최소 거리(제일 적게 블럭을 밟아서 이동)를 묻는 문제인줄 알고 풀었다.

✔️틀렸지만 작성한 코드 설명
1. path로 2차원 리스트를 만들어 0으로 채우고, 물 웅덩이를 -1로 채운다.
2. 시작 위치는 [0, 0]이므로 queue에 미리 넣어두고 x, y가 각 이동할 위치인 xx, yy를 만든다.
(xx, yy를 이용해서 위, 아래, 양 옆으로 이동한다.)
3. queue에 아무것도 없을 때까지 왼쪽 하나를 제거하여 범위에 있고, 물 웅덩이가 아니고 0인 경우, queue에 추가한다.
4. path[new_x][new_y] = path[x][y]에 하나를 더한다.

[#Error]solution함수_python

:: 문제 잘못 읽었다..... 최소 거리를 구하는 풀이를 했는데 경로의 개수를 구하는 문제였따...

from collections import deque

def solution(m, n, puddles):
    path = [[0] * m for _ in range(n)]
    for p in range(len(puddles)):  # 장애물 표시
        path[puddles[p][0] - 1][puddles[p][1] - 1] = -1
    queue = deque()
    queue.append([0, 0])
    path[0][0] = 1

    xx = [0, 1, 0, -1]
    yy = [1, 0, -1, 0]

    while queue:
        now = queue.popleft()
        x = now[0]
        y = now[1]
        for i in range(4):
            new_x = x + xx[i]
            new_y = y + yy[i]
            if 0 <= new_x < n and 0 <= new_y < m:
                if path[new_x][new_y] != -1 and path[new_x][new_y] == 0:
                    queue.append([new_x, new_y])
                    path[new_x][new_y] = path[x][y] + 1

    return min(path[-1][-2], path[-2][-1])-1

[#Clone] solution함수_python

✅ 하나씩 이동하면서 해당 위치까지 갈 수 있는 방법을 저장해둔다.

1. path라는 2차원 리스트를 이용해서 길을 만든다.
2. [1, 1]에서 출발하므로 path[1][1] = 1로 만들어 두고 for문을 이용하여 순서대로 이동한다.
3. i = 1, j = 1인 경우는 집위치 이므로 넘어간다.
4. puddles에서 주어진 물 웅덩이의 위치와 for문에서는 좌표가 반대이므로 [j, i]가 있으면 갈 수 없으므로 0으로 만들어준다.
5. 해당 위치까지 올 수 있는 방법은 순서대로 이동했기 때문에 위에서 오는 방법과 왼쪽에서 오는 경우를 더해주면 된다.
6. 마지막에 학교가 위치해 있으므로 path[-1][-1]이 정답이다.

def solution(m, n, puddles):
    path = [[0]*(m+1) for _ in range(n+1)]
    path[1][1] = 1
    for i in range(1, n+1):
        for j in range(1, m+1):
            if i == 1 and j == 1:
                continue
            if [j,i] in puddles:
                path[i][j] = 0
            else:
                path[i][j] = path[i-1][j] + path[i][j-1]

    return path[-1][-1]%1000000007

clone함수 출처