[백준 1018번] 체스판 다시 칠하기 with Java

guswls·2024년 4월 23일

백준 브루트포스

알고리즘

목록 보기

5/39

문제

https://www.acmicpc.net/problem/1018

코드

import java.io.*;
import java.util.*;

class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		String[][] map = new String[N][M];

		for (int i = 0; i < N; i++) {
			String[] input = br.readLine().split("");
			for (int j = 0; j < M; j++) {
				map[i][j] = input[j];
			}
		}

		System.out.println(solve(N, M, map));
	}

	static int solve(int N, int M, String[][] map) {
    	//첫번째로 흰색이 나오는 경우와 검은색이 나오는 경우, 두가지로 나눔.
		String[] whiteLine = { "W", "B", "W", "B", "W", "B", "W", "B" };
		String[] blackLine = { "B", "W", "B", "W", "B", "W", "B", "W" };

		//N-7, M-7까지로 범위를 정한 이유는 8 X 8범위에 대해 고려해야하기 때문이다.
        //예를 들어 N이 9라면, [0 ~ 7], [1 ~ 8] 총 두 경우를 고려할 수 있다.
		int result = Integer.MAX_VALUE;
		for (int w = 0; w < N - 7; w++) {
			for (int h = 0; h < M - 7; h++) {
				int count = 0;
				
                //whiteLine과 blackLine을 번갈아가며 비교하기 위한 플래그
				boolean isCheck = false;
				for (int i = w; i < w + 8; i++) {
                	//비교할 패턴의 인덱스
					int idx = 0;
					for (int j = h; j < h + 8; j++) {
                    	//패턴에서 기대한 색깔과 다른 경우, count를 더함.
						if (!isCheck) {
							if (!whiteLine[idx].equals(map[i][j])) {
								count++;
							}
						} else {
							if (!blackLine[idx].equals(map[i][j])) {
								count++;
							}
						}
						idx++;
					}
                    //한 줄을 모두 검사할 때 마다 플래그를 바꾸어 번갈아가며 패턴을 갖도록
					isCheck = !isCheck;
				}

				//64 - count는 나올 수 있는 다른 패턴을 만들기 위한 개수를 의미함
                //예를 들어 검은색부터 시작하는 체스판을 만들 때 하나만 변경해도 됐다면
                //흰색부터 시작하는 체스판으로 만드려면 그 하나의 칸을 제외한 모든 칸을 변경해야 함.
				int curResult = Math.min(count, 64 - count);
				result = Math.min(result, curResult);
			}
		}

		return result;
	}
}

이번 문제의 경우, 알아두어야 코드 요소가 많기 때문에 주석으로 상세하게 설명함.

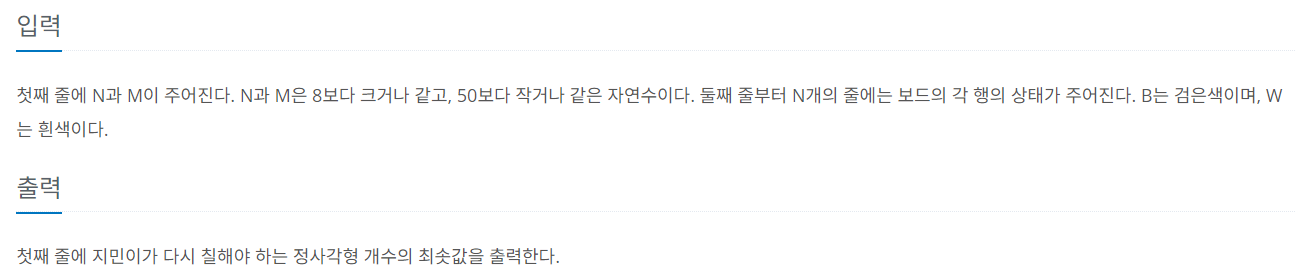
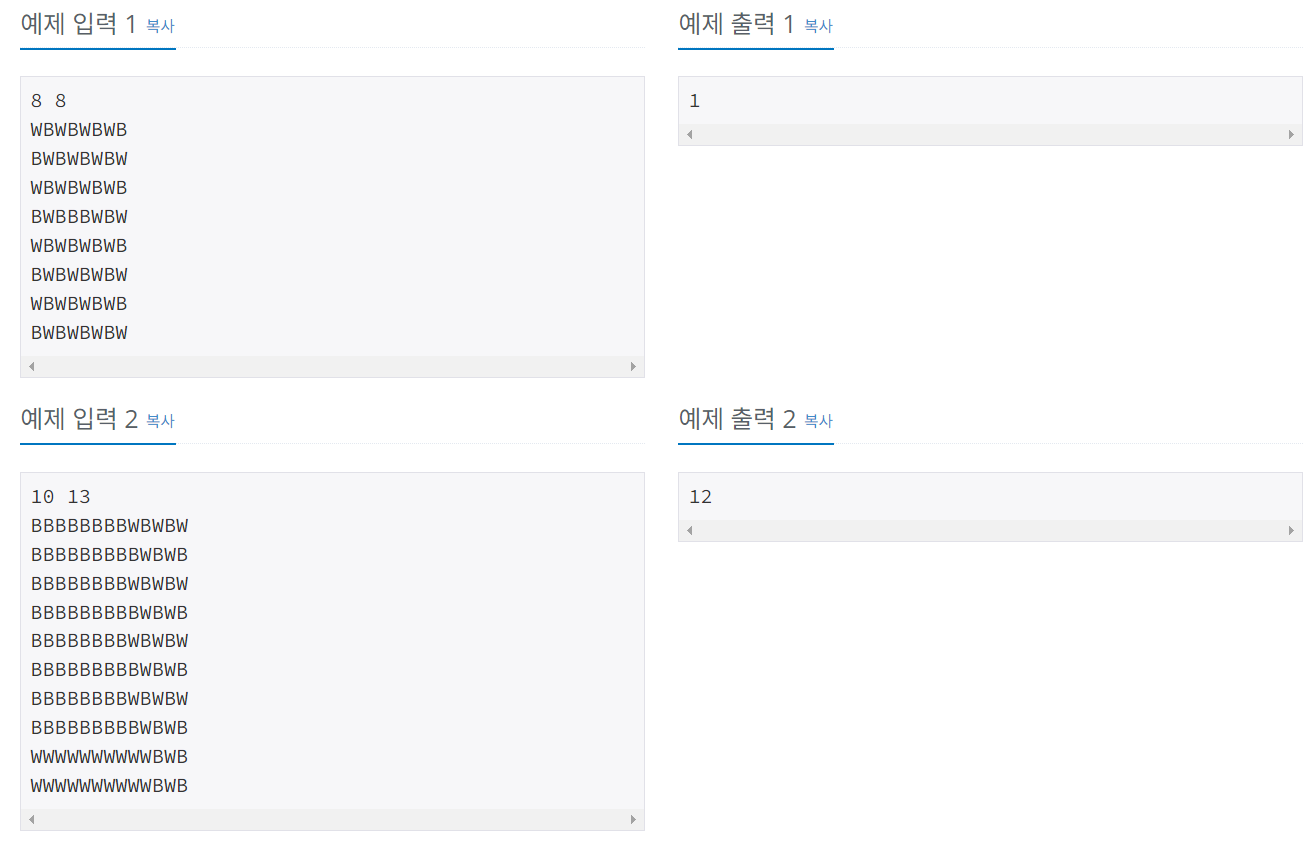
문제 이해

N X M 크기의 2차원 배열에서 8 X 8크기의 영역을 선택한다.
그 영역이 체스판 형태가 되도록 색을 변경한다.
체스판 형태는 B와 W가 번갈아서 나타나는 형태를 의미한다.
8 X 8영역을 골라 체스판 형태를 만들 수 있는 최소 색깔 변환 횟수를 구하는 문제이다.

풀이 방법

체스판의 한 라인을 구성하고 있는 경우는 다음의 두가지와 같다.
1) B W B W B W B W
2) W B W B W B W B
체스판은 위의 1번 패턴과 2번 패턴이 번갈아 나타나게 된다.
또한 1번 패턴 -> 2번 패턴, 2번 패턴 -> 1번 패턴과 같이 순서가 변경될 수도 있다.
위 사항들을 고려하여, 만들 수 있는 모든 8 X 8배열에 대해 변경 회수를 구하고 그중 최소 값을 구하면 된다.
그 외의 코드적인 부분은 따로 주석에 자세히 달아두었다.

핵심 포인트

체스판은 흰색부터 시작하는 경우와 검은색부터 시작하는 경우, 두 경우가 존재할 수 있다.
만약 검은색으로 시작하는 체스판을 만들기 위해 2번의 변경만 필요하다면, 흰색으로 시작하는 체스판은 그 2개의 칸을 제외한 모든 칸을 변경해야 한다. 따라서 64 - 2 = 62가 변경이 필요한 회수이다.
이를 이용하면, 두 경우를 모두 구할 필요 없이 한 경우만 구해도 된다.
N개의 배열에서 8개씩 순차적으로 탐색한다고 가정하면 범위를 N - 7로 설정할 수 있다.

보완할 점 / 느낀 점

첫 접근때는 단순히 흰색과 검은색의 개수가 같기만 하면 되는줄 알았다. 하지만, 예제 입력 6을 테스트하면 알 수 있듯이 개수가 같아도 다른 경우가 존재한다.
따라서 브루트포스로 해결할 수 밖에 없었는데 번갈아가며 똑같아야한다는 것이 매우 까다로웠다.
그래서 결국 풀이를 참고해서 문제를 해결할 수 있었다.
핵심 아이디어는 결국 8 X 8크기로 만들 수 있는 두 종류의 체스판을 만들기 위해 각각 필요한 변경 회수를 구하는 것었다.
그 외에 배열의 탐색 범위를 N-7로 정하는 것과 같은 개념은 다른 문제를 풀 때도 유용할 것 같았다.
좋은 문제였다고 생각하며, 꼭 다시 풀어봐야겠다.