문제
https://www.acmicpc.net/problem/1932
코드
import java.io.*;
import java.util.*;
class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] arr = new int[N + 1][N + 1];
int[][] dp = new int[N + 1][N + 1];
for (int i = 1; i < N + 1; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 1; j < i + 1; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < i + 1; j++) {
dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i - 1][j]) + arr[i][j];
}
}
int result = Arrays.stream(dp[N]).max().getAsInt();
System.out.println(result);
}
}문제 이해
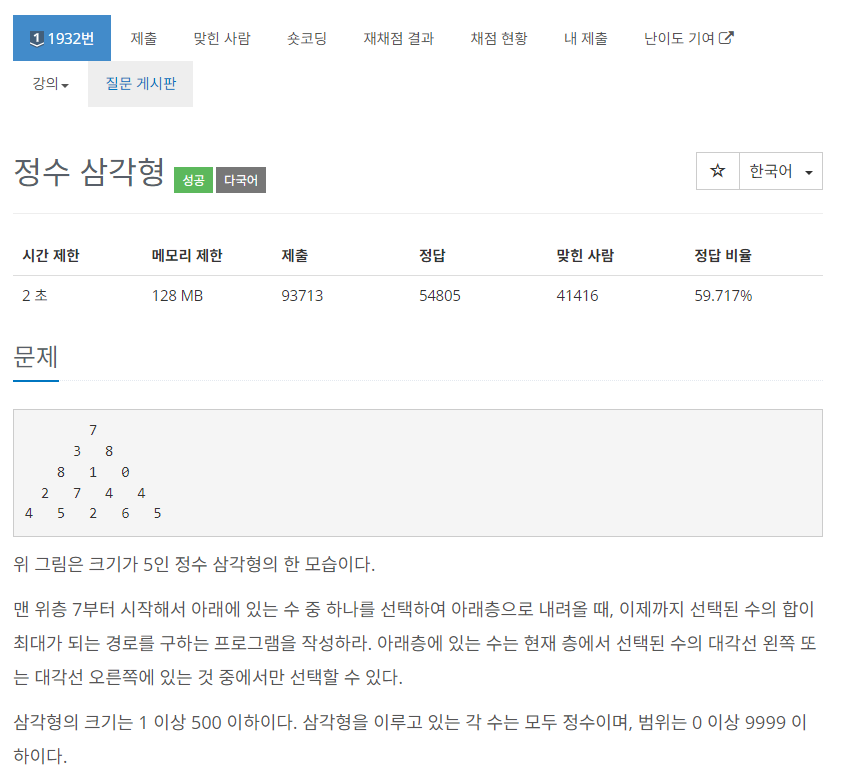
- 위 문제 사진과 같이 정수로 이루어진 삼각형이 주어진다.
- 첫번째 꼭지점에 위치한 값부터 시작하여 밑으로 내려간다. 이떄 내려갈 때는 대각선 좌, 우 만을 선택할 수 있으며 선택한 값들의 합이 가장 최대가 되어야 한다.
풀이 방법
- 언뜻 봤을 떈 단순히 그리디, 즉 각 마다 왼쪽, 오른쪽 값을 비교하여 그 중 더 큰수를 선택하는 문제처럼 보인다.
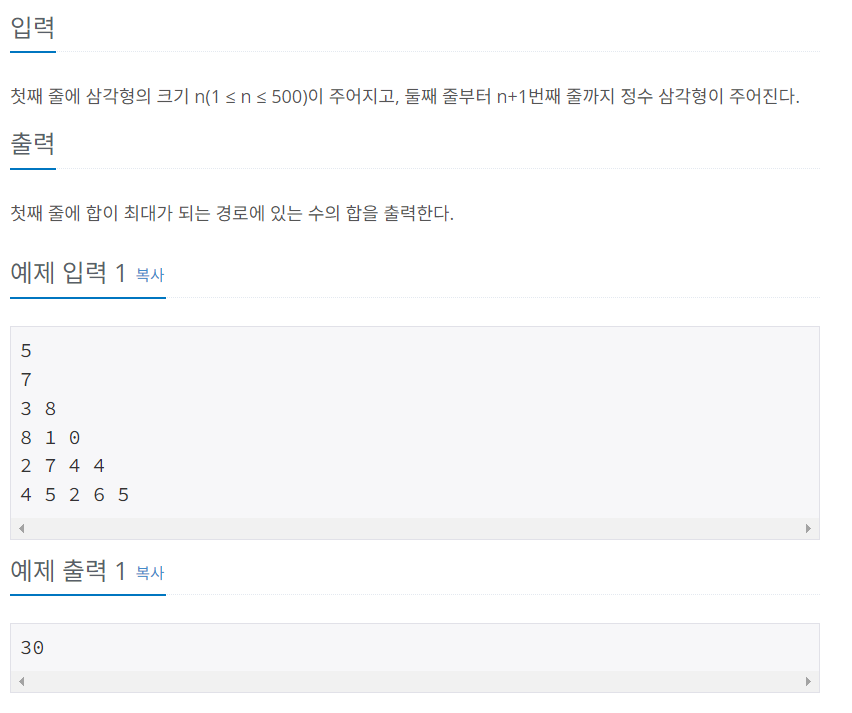
- 하지만 문제의 예시로 계산해보면 알겠지만, 그리디한 방법은 항상 최대값을 보장하지 않는다. (문제 예시의 경우, 그리디하게 답을 구하면 28이 나와 오답이 나온다)
- 따라서 모든 경우를 구하고 그중 최대값을 구하는 방식, 즉
dp로 풀어야한다. - 위 코드의 경우는 경계조건을 고려하지 않고 점화식만을 이용하여 푼 문제이다.
- 삼각형의 모든 값을 순회하며 점화식을 활용해 dp배열을 갱신한 해나가면, dp배열의 마지막 행이 각 경우의 합이 된다.
- 그 합들 중 최대값을 구하면 된다.
핵심 포인트
dp로 풀어야된다는 것을 알았으면, 핵심은 점화식이다. 각 삼각형의 위치를 인덱스로 나타내면 다음과 같다.
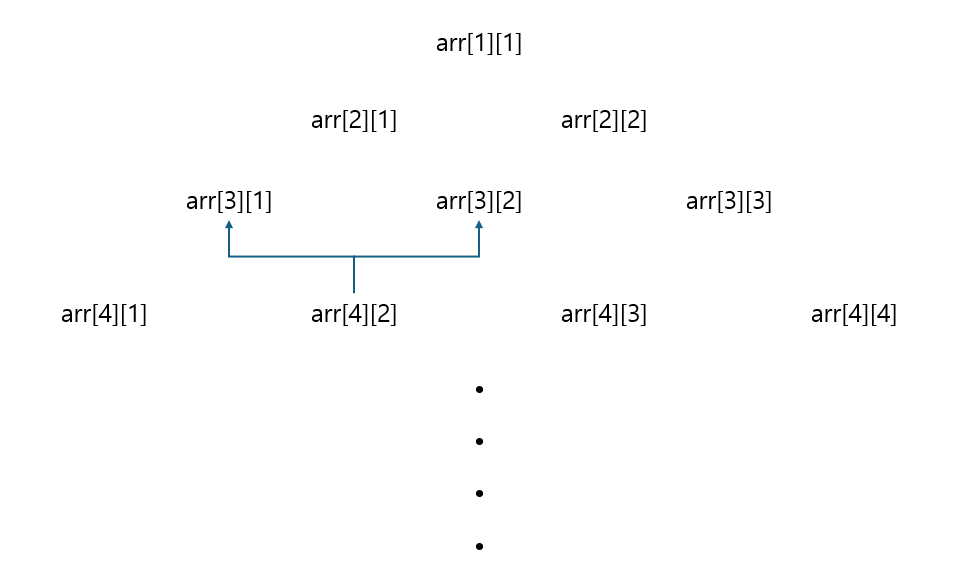
arr[4][2]에서의 최대값은arr[3][1]까지의 합과arr[3][2]까지의 합중에 더 큰 값을arr[4][2]에 더한 값이다.- 즉, 이전 층의 왼쪽 합과 오른쪽 합 중 더 큰 값을 현재 값과 더하면 현재 경우에서 구할 수 있는 최대값이 된다.
- 따라서 이를 점화식으로 뽑아내면 코드에서처럼 아래의 점화식이 나오게 된다.
dp[i][j] = arr[i][j] + Math.max(dp[i-1][j], dp[i-1][j-1])
보완할 점 / 느낀 점
dp인줄 모드고그리디로 풀었다가 뒤늦게 깨달은 문제였다.dp문제를 처음 풀어보는 것이었기에, 친구의 도움을 많이 받아서 해결할 수 있었다.- 문제를 다 이해한 다음에야 정말 naive하게 경계조건을 고려하지 않고 위의 코드처럼 짤 수 있었다.
- 다른 알고리즘에 비해
dp를 아직 공부하지 않았기 때문에,dp문제에 대해서도 꾸준히 풀어봐야겠다.
참고자료
경계조건을 고려한 코드
import java.io.*;
import java.util.*;
class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] arr = new int[N][N];
int[][] dp = new int[N][N];
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < i + 1; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
dp[0][0] = arr[0][0];
for (int i = 1; i < N; i++) {
for (int j = 0; j < i + 1; j++) {
if (j == 0) {
dp[i][j] = arr[i][j] + dp[i - 1][j];
} else if (j == i) {
dp[i][j] = arr[i][j] + dp[i - 1][j - 1];
} else {
dp[i][j] = arr[i][j] + Math.max(dp[i - 1][j], dp[i - 1][j - 1]);
}
}
}
int result = Arrays.stream(dp[N - 1]).max().getAsInt();
System.out.println(result);
}
}수행시간 비교

- 위에 제출이 경계조건을 고려한 코드이고, 아래 조건이 고려하지 않은 코드이다.
- 입력값이 기본적으로 작고, 결국 O(N^2)의 시간복잡도를 가지는 풀이들이기에 별 차이는 없는 것으로 보인다.
- 하지만 핵심포인트와 같이 그림을 좀만 그려보면 경계조건을 금방 캐치할 수 있기 때문에, 입력이 더 커지는 경우를 고려해서 경계조건을 잡는 연습도 해야겠다.
