문제

---

https://www.acmicpc.net/problem/9095

코드

---

class Main {
	static StringBuilder sb = new StringBuilder();

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());

		for (int i = 0; i < N; i++) {
			solve(Integer.parseInt(br.readLine()));
		}

		System.out.println(sb);
	}

	static void solve(int num) {
		int[] dp = new int[11];
		dp[1] = 1;
		dp[2] = 2;
		dp[3] = 4;

		for (int i = 4; i <= num; i++) {
			dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
		}

		sb.append(dp[num]).append("\n");
	}
}

문제 이해

---

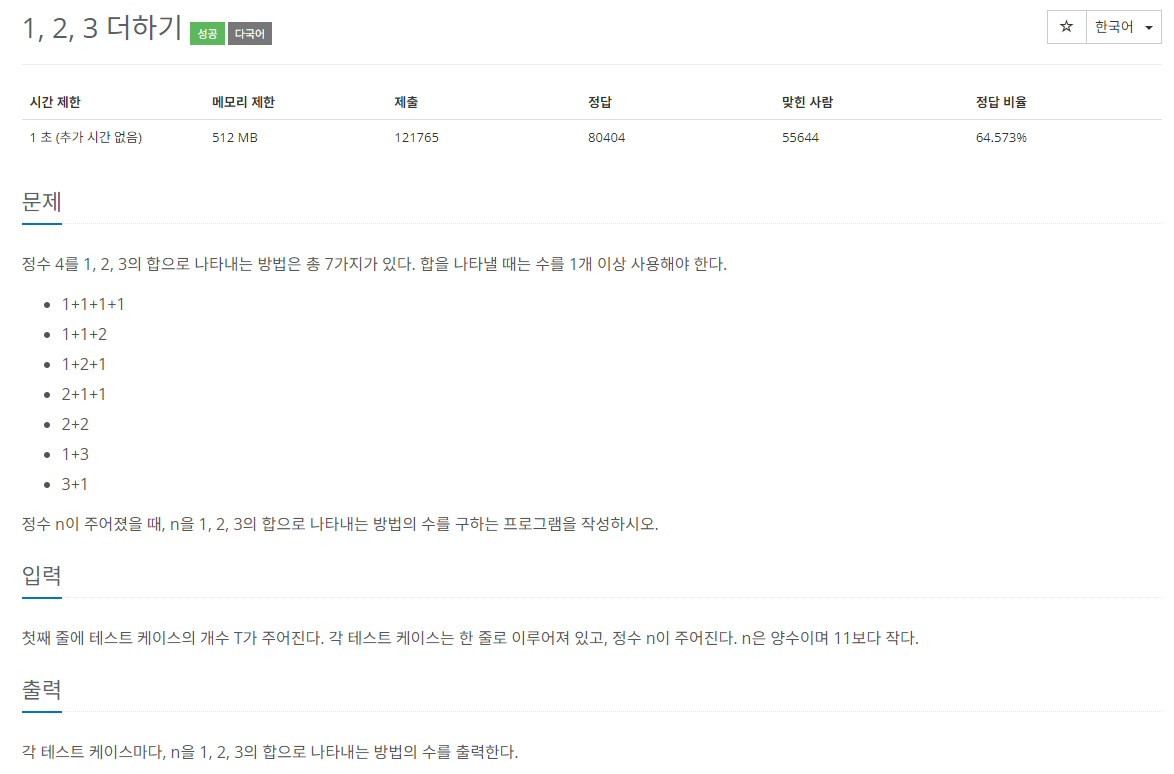
• 문제는 단순하다. 1, 2, 3을 더해서 n을 만들 수 있는 조합의 개수를 구하면 된다.
• 이때 순서가 같은 수로만 이루어졌더라도, 다른 조합으로 생각한다. 예를 들어 1 + 3은 3 + 1과 다르다.

풀이 방법

---

• 1부터 3까지 만들 수 있는 경우의 수를 생각하면 다음과 같다.
• 1은 1개, 2는 2개, 3은 4개가 있다.
• 4는 7개의 조합이 있으며, 5도 따져보면 13개가 있다.
• 즉, 만들 수 있는 조합의 개수를 dp테이블에 저장한다고 했을 때 n이 4이상인 경우에 한해서는 dp[n] = dp[n-3] + dp[n-2] + dp[n-1]을 만족한다.
• 위 점화식을 코드에 그대로 적용하면 된다.

핵심 포인트

---

• 위에서 말한 규칙성을 파악하고 문제에 적용하는 것이 핵심이다.

보완할 점 / 느낀 점

---

• 이전에 dp문제를 풀었던 경험으로 조합의 개수를 구하는 방법에 대해 생각해보았으나, 위 규칙을 찾지 못하고 결국 문제를 찾아봤다.
• dp문제는 계속 풀어도 익숙해지지 않는 것 같다.
• 단순히 많이 풀어보는 것 이외에는 답이 없어보인다.. 이 문제 역시 다시 풀어봐야겠다.

참고자료

---

• https://lotuslee.tistory.com/43