아래 문제를 풀다가 이중 for문으로 풀었는데, 계속해서 시간초과가 났다.
문제 보러가기

다른 사람 코드를 참고하다가, 누적합 개념을 알아야 풀 수 있다고 해서 정리해본다.
누적합은 Memorization기법이다. 그래서 DP 문제 풀이에 적합하다.
그냥 눈으로 보면 이해가 잘 안가는데, 색칠해보면서 직접 해보면 큰 도움이 됩니다!!
1차원 누적합
1차원 누적합은 간단하다.

기존에 Array가 있으면 누적합은 처음부터 끝까지의 합이다
 식으로 나타내면 다음과 같다.
식으로 나타내면 다음과 같다.Sum_Array[i] = Sum_Array[i-1] + Array[i]
예를 들어보자
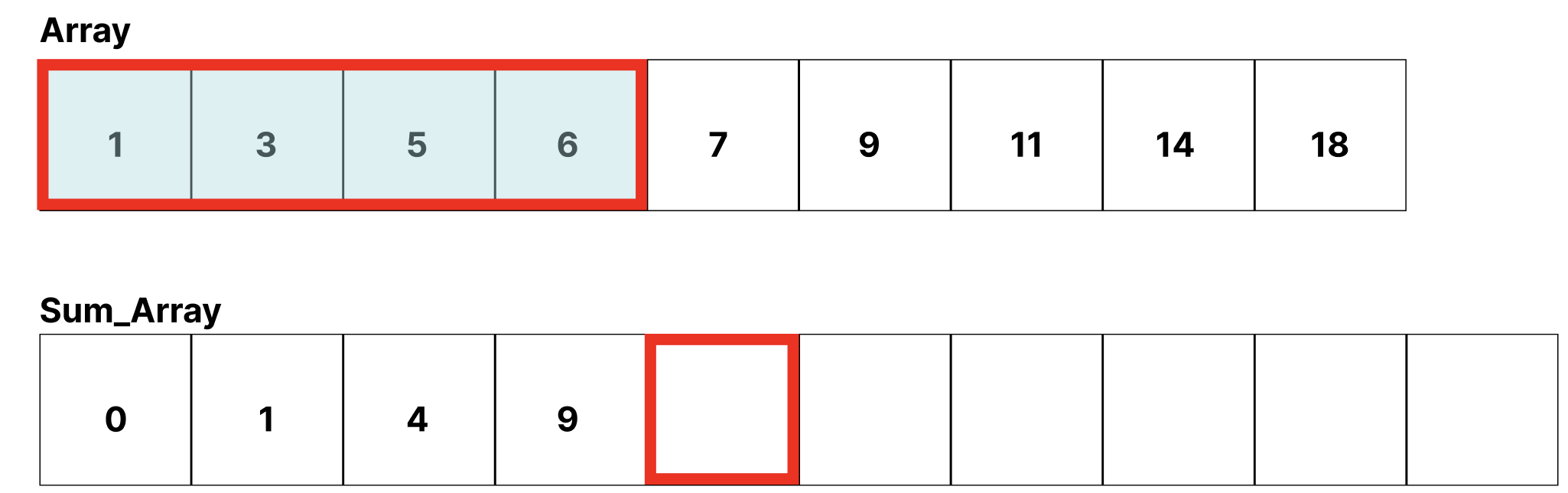
Sum_Array[4] = Array[1] + Array[2] + Array[3] + Array[4] 이다.
하지만, Array[1] ~ Array[3] 은 Sum_Array[3]이다.
다시 구해보면 다음과 같다.
Sum_Array[4] = Sum_Array[3] + Array[4]
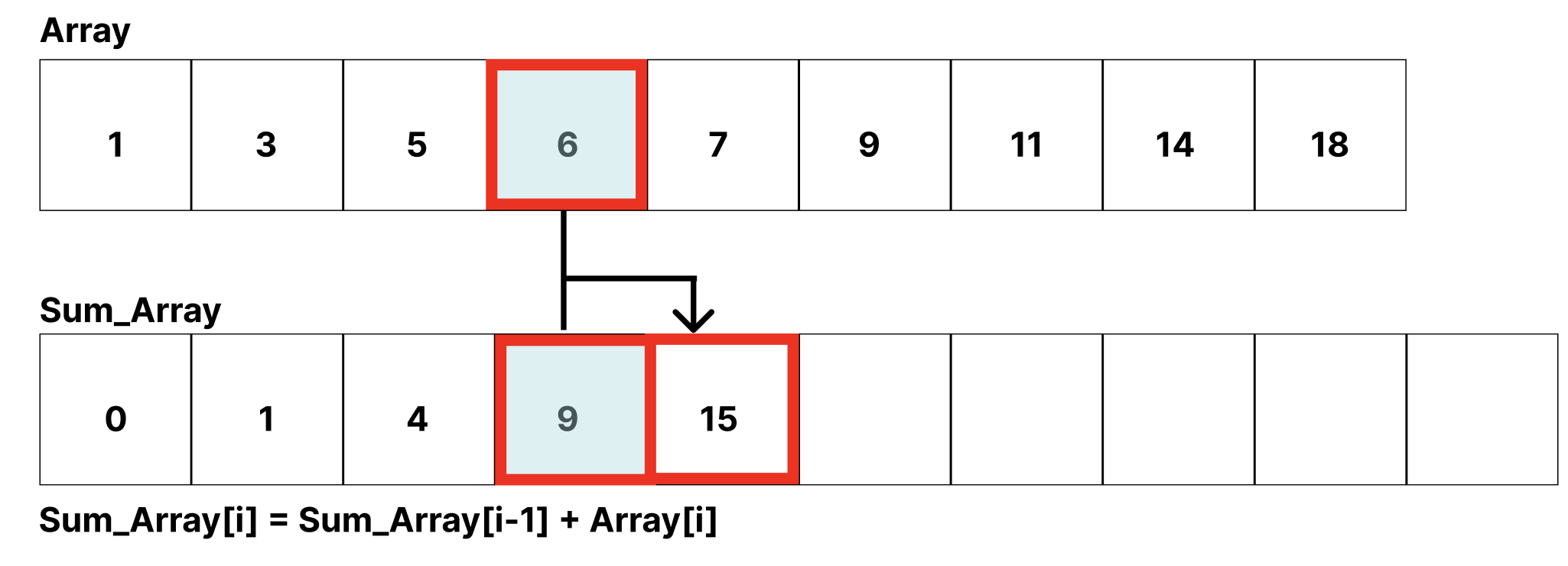
다음과 같은 식이 성립되는 것이다.
2차원 누적합
그렇다면 2차원은 누적합은 어떻게 될까? 예시를 보자.
1차원 누적합 처럼, 모든 합을 나열해두고, Memorization할 수 있는 것을 찾아보자.
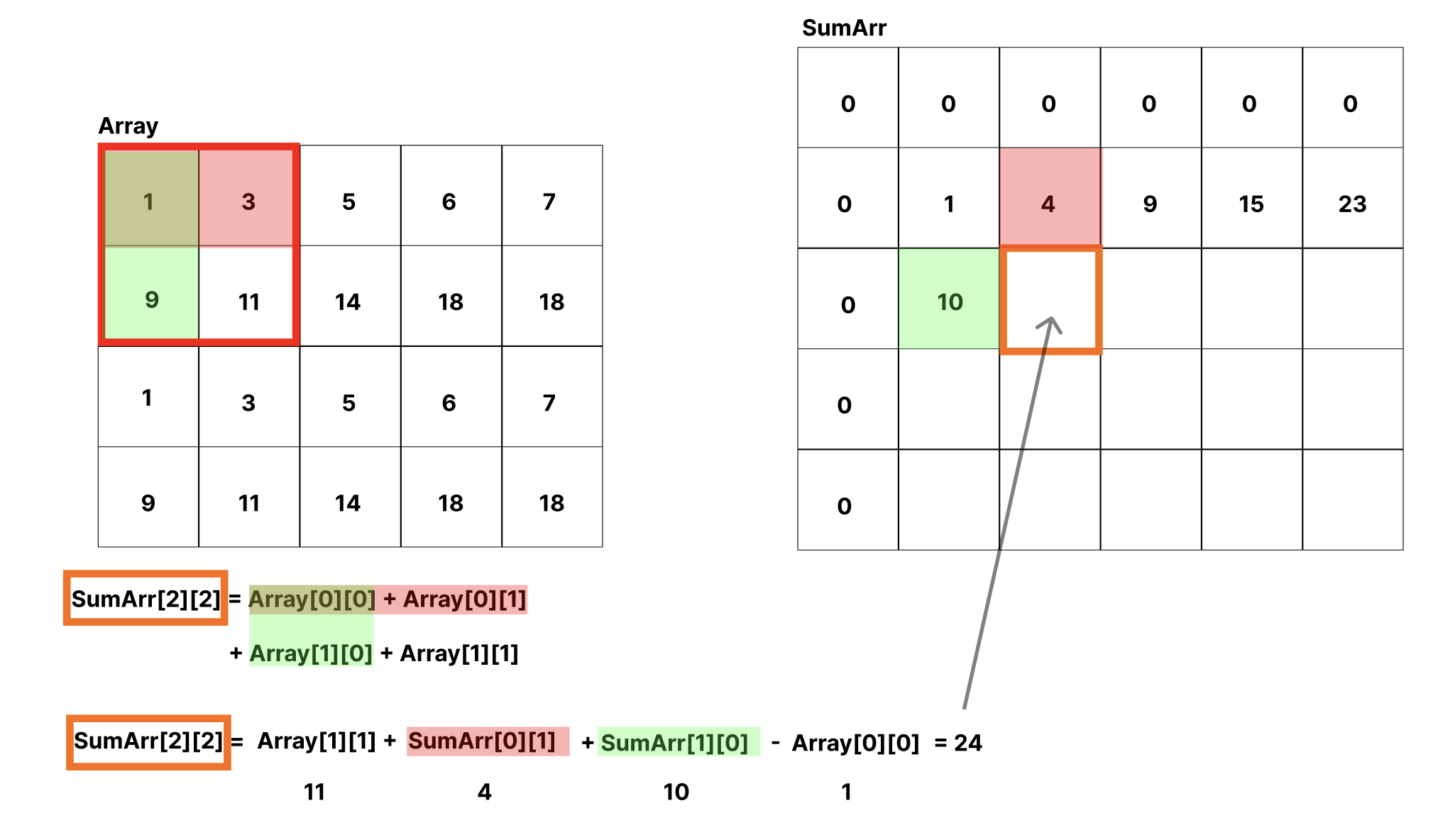
묶을 수 있는 것을 묶어보면 다음과 같다.
그러면 2 X 2가 아닌, 더 커진 배열에 대해서 알아보자.
3 X 3 배열에 대해서는,
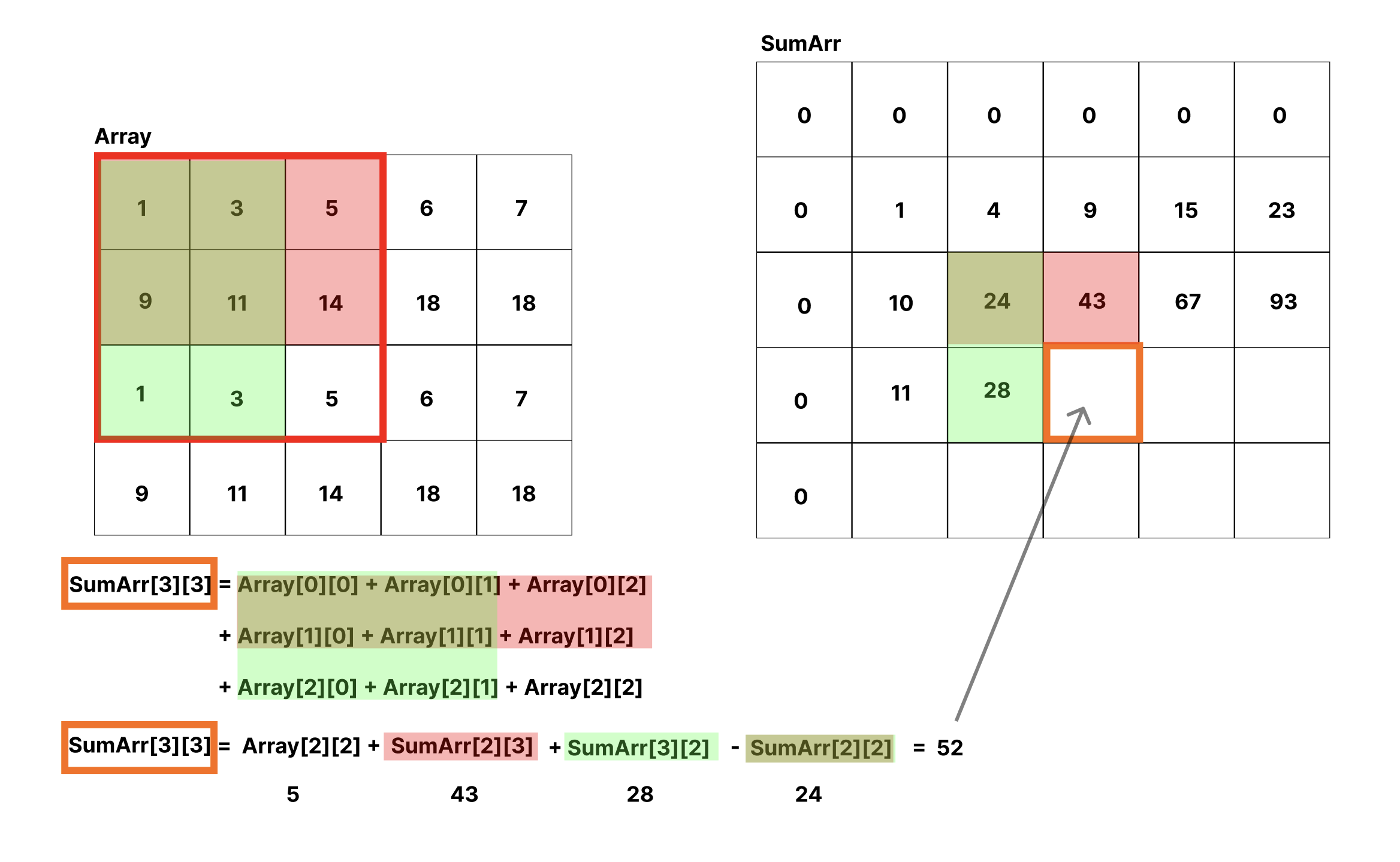
Sum으로 묶인 부분에 대해서 더하고, 겹친 부분은 뺀다. 다음과 같은 규칙을 볼 수 있다.
Array해당 칸 + Sum배열에서 바로 윗 칸 + Sum배열에서 바로 옆 칸 - Sum배열에서 바로 대각선 칸
식으로 구해보면, 다음과 같다.
sumArr[i][j] = arr[i-1][j-1] + sumArr[i-1][j] + sumArr[i][j-1] - sumArr[i-1][j-1]
이 개념을 사용하면 성능을 더 높일 수 있다.
그렇다면 특정한 좌표에서 특정한 좌표까지의 합을 구할 수 있을까?
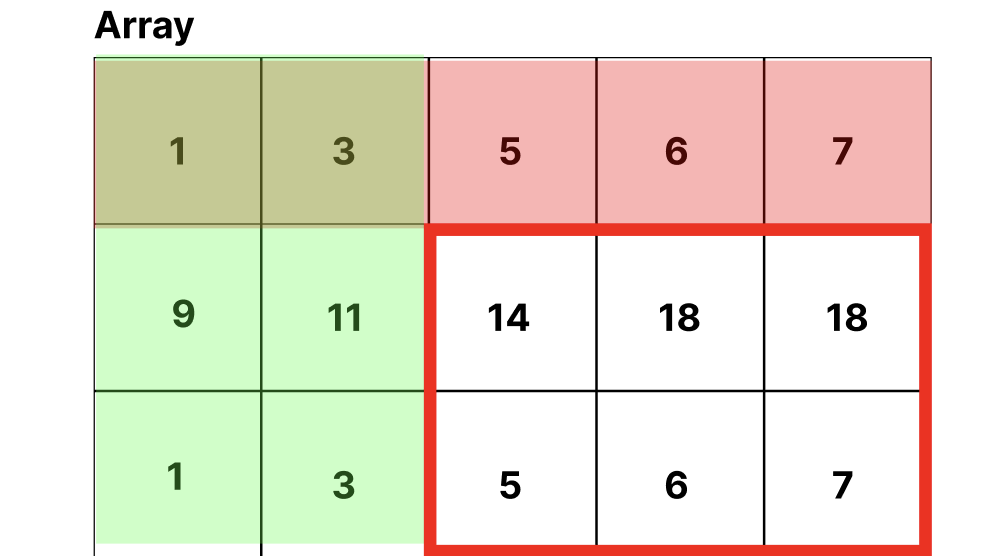
[x1, y1] = [1, 2][x2, y2] = [2, 4]
전체 SumArr[3][5]
(-) SumArr[1][5]
(-) SumArr[3][2]
(+) SumArr[1][2]
이걸 식으로 나타내면 다음과 같다.
SumArr[x2+1][y2+1] - SumArr[x1][y2+1] - Sum[x2+1][y1] + SumArr[x1][y1]
