
둘 중에 하나
가장 흔한 예시가 Up & Down 게임이다.
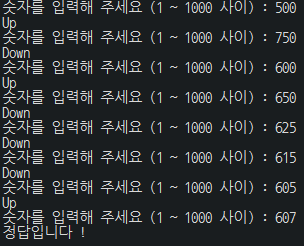
보통 Up & Down 게임을 하면, 중간 지점을 얘기하여 근접하게 소거한다.
1 ~ 1000 사이면, 500을 이야기 하여 남은 구간에 대해서 또 절반을 고려한다.
이런 중간점 탐색 방식인 이진 탐색에 대해 알아보자.
이진 탐색
정렬되어 있는 데이터에서 중간점에서 나누어 탐색하는 방법
- 이진 탐색은 정렬 된 데이터에서 절반으로 계속해서 나누며 탐색하는 방법이다.
- 정렬되지 않은 데이터는 절대 이진 탐색을 사용할 수 없다.
- 절반으로 계속해서 나누기 때문에 시간 복잡도는
O(logN)이다.
배열로 구현한 경우
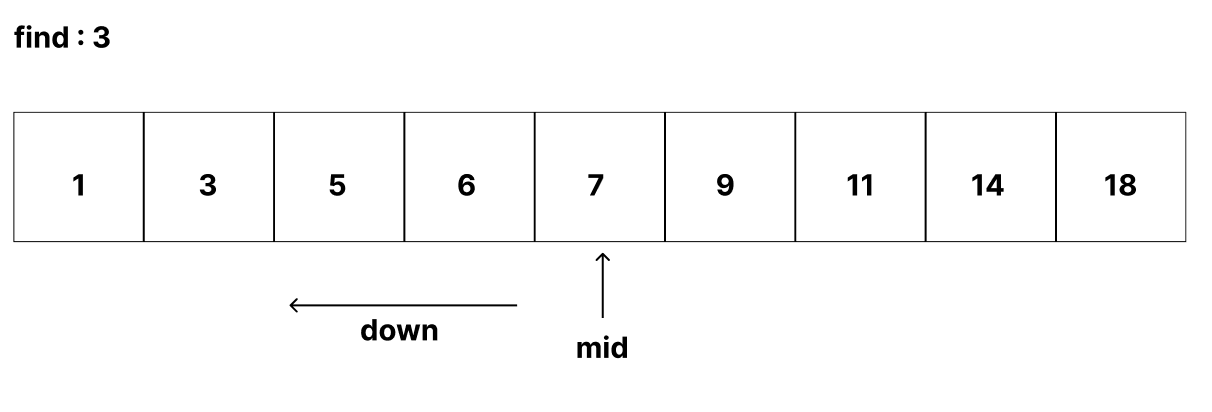
아래와 같은 배열에서 3을 찾아야 할 때, 다음과 같은 과정을 거친다.
1. 중간 값을 구해서, 그 값보다 작은지 큰지 비교한다.
- 작으면
list[:mid]에 대해서 중간 값을 찾는다.
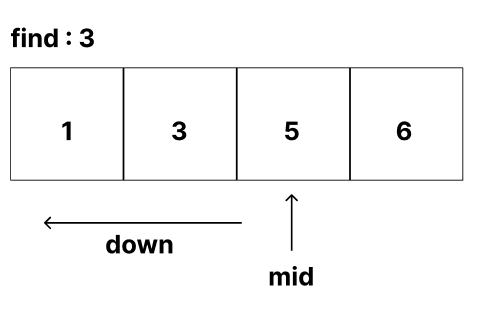
2. SubList에 대해서 다시 비교한다. 중간 값보다 더 작으니 새로운 list[:mid]로 SubList를 만든다.
3. 값이 같으면 index를 리턴한다.
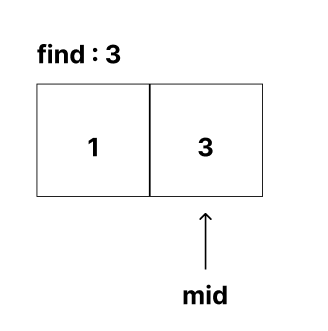
이 처럼 중간 값에 대해서 SubList를 만들고 비교한다.
위와 같이 데이터가 작은 경우에는 효율적이지 않을 수 있다.
왜냐하면 정렬의 시간 복잡도는 O(nlogn)이고, 이진 탐색의 시간 복잡도는 O(logn)이기에 결국 O(logn)이 된다.
하지만 일반적인 반복문을 이용한 시간 복잡도는 O(n)이기에, 이진 탐색을 위해 정렬을 하는 경우라면 순차 탐색이 더 유리할 수도 있다.
또한 큰 값에 대해서 비교하는 것이 더 좋기 때문에 잘 고려해야한다.
트리에서의 이진 탐색
트리에서의 이진 탐색은 BST (이진 탐색 트리)에서만 가능하다.
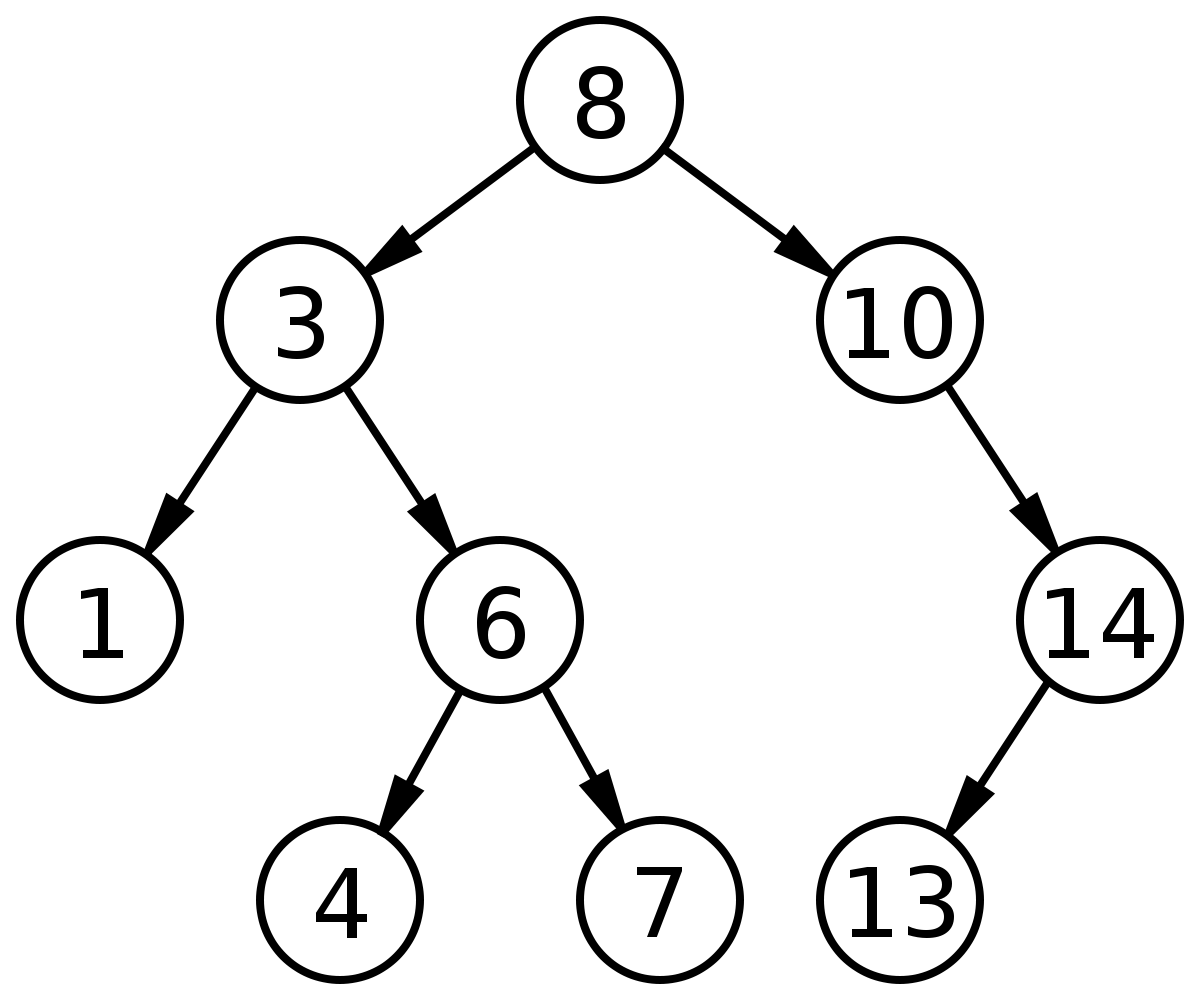
부모 노드에서 왼쪽으로 가면 작은 값, 오른쪽으로 가면 큰 값으로 탐색이 가능하다.
이렇게 값을 분할하여 탐색이 가능하므로, 트리에서도 탐색이 가능하다.
이진 탐색 장점
- 최악일 때도
O(logn)을 보장한다. O(logn)을 보장하므로, 많은 데이터에서 더 효과적이다.
순차 탐색보다 더 빠르게 데이터를 탐색할 수 있어서 효과적이다.
이진 탐색 단점
-
정렬이 되어있지 않으면 사용이 불가하다.
앞서 말했지만 작은 데이터에 대해서 정렬을 하고 이진 탐색을 하면O(nlogn)의 시간 복잡도가 나올 수 있다. 그렇게 되면, 차라리 순차 탐색이 더 나을 수 있으므로 잘 고려하여 탐색 방법을 선택해야 한다. -
계속해서 변화하는 데이터라면 적합하지 않다.
지속적으로 변화하는 데이터는 삽입/삭제할 때마다 정렬을 해주어야한다. 이로 인한 시간이 더 오래 걸릴 수 있으므로 조심해야 한다.
