[알고리즘] 완전 탐색

전현준·2024년 7월 12일

algorithm

Algorithm

목록 보기

7/13

1. 완전탐색 알고리즘이란?

완전탐색은 간단히 가능한 모든 경우의 수를 다 체크해서 정답을 찾는 방법이다.
즉, 무식하게 반복문과 조건문을 이용하여 모든 경우의 수를 다 확인한다.

이 방법은 무식하게 한다는 의미로 "Brute Force"라고도 부르며,
직관적이어서 이해하기 쉽고 문제의 정확한 결과값을 얻어낼 수 있는 가장 확실하며 기초적인 방법이다.

예를 들어, 4자리의 암호로 구성된 자물쇠를 풀려고 시도한다고 생각해보자. 이 자물쇠가 고장난 것이 아니라면, 반드시 해결할 수 있는 가장 확실한 방법은 0000 ~ 9999까지 모두 시도해보는 것이다.(최대 10,000번의 시도로 해결 가능)

이렇게 구현이 생각보다 간단하며 답이 존재한다면 경우의 수에 따라서 실행 시간이 비례한다.

알고리즘에서 구현을 통해서 문제를 해결하는 것도 중요하지만, 효율적으로 동작하는가도 중요하다.
같은 방식을 "어떻게 더 시간 복잡도를 줄일 수 있을까"를 고민하는 것도 중요하다.

예를 들어 보자
List를 반복문을 돌면서, List가 Empty할 때까지, 최댓값을 하나씩 pop하는 코드를 짜보자.

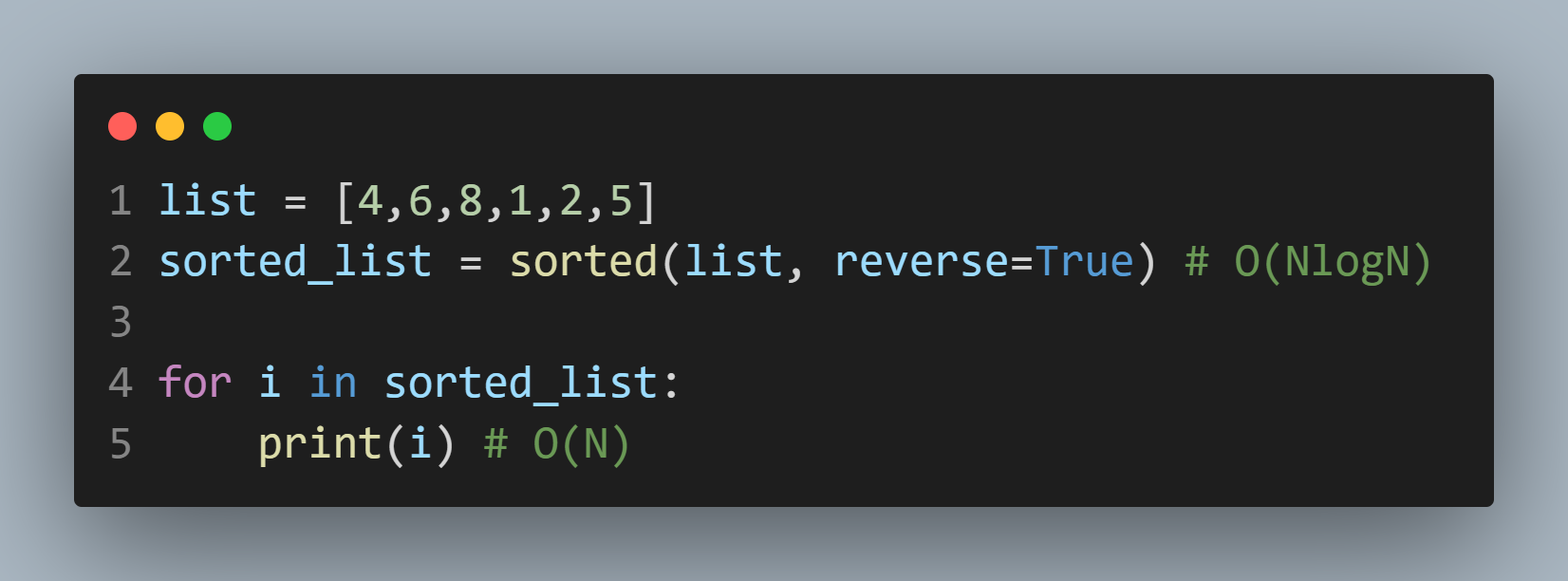
반복문과 `max` 찾기	정렬된 리스트에서 하나씩 추출

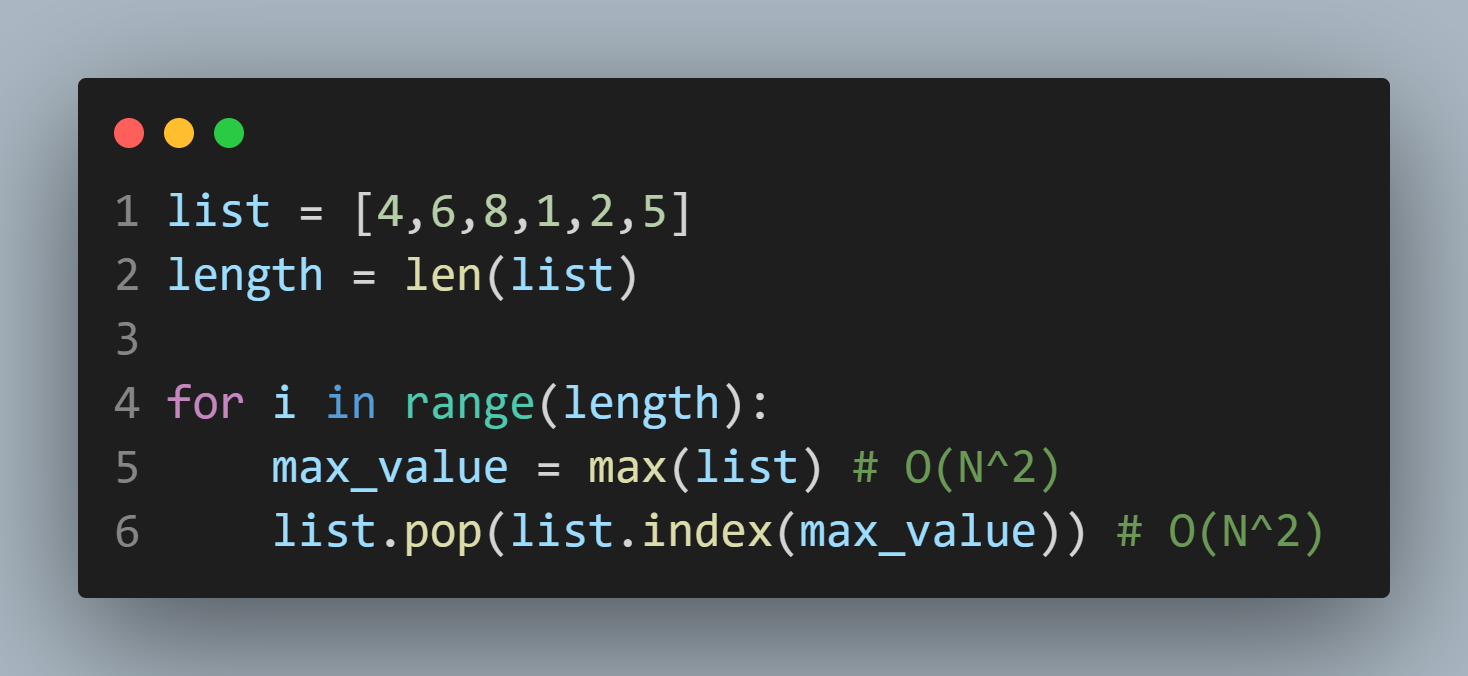두 코드의 차이를 보자.
두 코드 모두 최댓값을 하나씩 찾아내는 코드이다.
같은 기능을 하지만, 왼쪽은 max 함수가 O(N)이기 때문에 반복문 내부에 있어 O(N^2)이다.

하지만 오른쪽 코드는 내림차순 정렬을 하고, 앞에서 부터 한개씩 추출한다.
이렇게 하면 정렬이 O(NlogN)이고, 반복문이 O(N)이기에 최종 O(NlogN)이 된다.

이렇게 같은 기능을 하는 코드이지만 다른 방식으로 시간 복잡도를 줄이는 방식을 생각하여야 한다.
완전 탐색은 모든 경우의 수를 다 파악하려면 시간 초과가 날 수 있으니, 다양한 방식을 사용해야 한다.

2. 완전 탐색 종류 파악하기

2-1. Brute Force

그냥 단순히 반복문과 조건문을 세워서 모든 경우의 수를 다 파악하는 것이 Brute Force이다.
예를 들어, 자물쇠 비밀번호를 맞출 때, 0000부터 9999까지 반복문을 통해서 맞추는 것을 말한다.

2-2. 순열

일단 순열을 이해하자.
수학이 가물가물해지고, 조합과 차이도 잘 기억이 안난다.

순열 : 서로 다른 n개에서 r개를 뽑아서 일렬로 나열하는 경우의 수
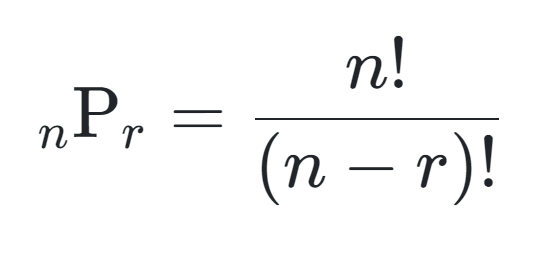
조합 : 서로 다른 n개에서 r개를 뽑아서 순서를 고려하지 않고 택하는 경우의 수

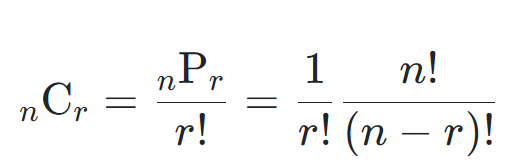
[a, b, c, d]를 가지고 있을 때 3개를 뽑는 경우

순열 : abc, acb, bac, abd .... (중복이 가능, 순서만 바뀌면 됨!)

조합 : abc, abd, acd, bcd (중복이 불가능)

이 차이를 이해하자. 순열이 순서에 대해서 모든 경우의 수를 구해야 하므로 완전 탐색이다.

어쨌든 순열은 이 순서를 구해야 한다.
N개의 데이터가 있을 때, 순열의 시간복잡도는 O(N!)이다.
O(N!)이면 N=10이면 360만번의 연산이 필요하고, N=11이면 4억번의 연산이 필요하다.

그래서 순열을 구하려면 N이 10보다는 작아야한다.

순열 Python Code

import itertools

arr = ['A', 'B', 'C']
nPr = itertools.permutations(arr, 2)
print(list(nPr))

결과 : [('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'C'), ('C', 'A'), ('C', 'B')]

Python은 순열 라이브러리가 존재한다. ~~하지만 자바는 없다는 소문이..~~

2-3. 비트마스크

비트마스크는 비트를 이용해서 연산하는 방법이다.

전공자라면 한번씩 2진수 계산을 해봤을 것이다.

AND (&)
- 11 & 10 → 10
OR (|)
- 11 | 10 → 11
NOT (!)
- !1 → 0
XOR (^) : 둘이 다르면 1, 같으면 0
- 11 ^ 10 → 01
SHIFT (<<, >>) : 한 칸씩 미루는 것
- >> 1011000 → 0101100

비트 연산은 O(1)이다.
그렇다고, 모든 값을 2진수로 변경하는 것은 추후 유지 보수 차원에서도 좋지 않다.

비트 마스크는 원소가 포함되거나, 포함되지 않는 두 가지 선택으로 구성되는 경우를 구할 수 있다.

예를 들어보자.
리스트에서 특정 원소가 포함되어 있는 경우를 알아보자.

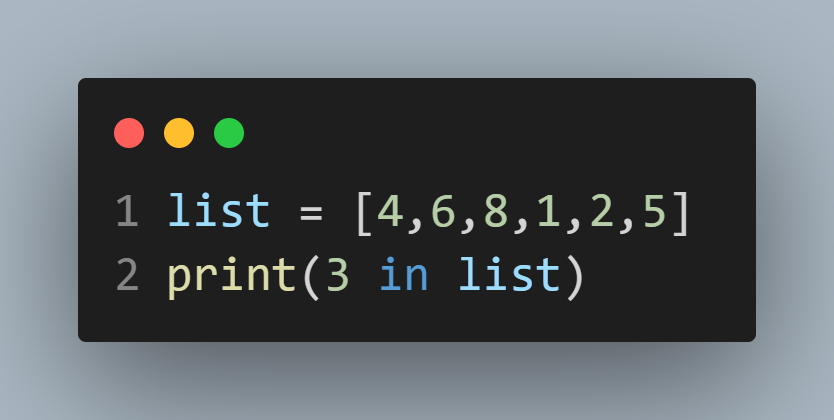
이 경우, List는 O(N)이다.
참고로 Set이나 Dictionary는 O(1)이다. 최악일 때는 O(N)이 될 수도..

하지만 비트 연산을 사용하면 O(1)로 찾아낼 수 있다.
내림 차순으로 비트를 표시해보자.

8	7	6	5	4	3	2	1	0
1	0	1	1	1	0	1	1	0

이렇게 나타내면 숫자로도 나타낼 수 있다. 101110110으로 나타낼 수 있으니
10진수로 변환하면 374로도 나타낼 수 있다.

그렇다면 아래와 같이 나타낼 수 있다.

원소가 포함되는 경우

여기서 4가 포함되어 있는지 확인하고 싶다면, 4와 AND를 하면 된다.

구분	8	7	6	5	4	3	2	1	0
`list`	1	0	1	1	1	0	1	1	0
AND (&)
`4`	0	0	0	0	1	0	0	0	0
결과	0	0	0	0	1	0	0	0	0

결과는 0000010000으로 나타났다. 0이 아닌 경우는 원소가 포함되어 있다.

원소가 포함되지 않는 경우

여기서 3이 포함되어 있는지 확인하고 싶다면, 3과 AND를 하면 된다.

구분	8	7	6	5	4	3	2	1	0
`list`	1	0	1	1	1	0	1	1	0
AND (&)
`3`	0	0	0	0	0	1	0	0	0
결과	0	0	0	0	0	0	0	0	0

결과는 0이 된다. 0이면 이 요소가 List에 존재하지 않는다는 것을 알 수 있다.

2-4 재귀 함수

재귀 함수는 비트 마스크와 마찬가지로, 각 원소가 두 가지 선택지를 가질 때 유용하다.

포함이 되면 해당 원소를 넣어 함수를 호출하고, 포함되지 않으면 그 상태에서 함수를 호출하는 등의 식

예를 들어, 4가지 숫자에서 2개를 선택하는 경우의 수를 고른다고 생각하자

반복문은 다음과 같다.

for i from 1 to 4..
    chose i
    for j from i+1 to 4..
        chose j
        print i j

하지만 값이 어마무시가 늘어나면 감당하기 힘들어진다.

재귀로 코드를 작성하면 어떨까?

def combination(n, k):
    # Base cases
    if k == 0 or k == n:
        return 1
    # Recursive step
    return combination(n-1, k-1) + combination(n-1, k)

# Calculate the number of combinations of 100 choose 5
result = combination(100, 5)
print(result)

가장 간단한 재귀이다.
10가지 숫자 중에서 3가지만 뽑는 경우의 수를 구하는 코드를 재귀로 작성하였다.

하지만 이 코드의 문제점이 있다. 시간 복잡도가 어마무시 하다는 것이다.
조합은 아래 단계의 값이 중첩되어 계산할 수 있는데, 계속해서 새로 값을 계산한다.

100가지 수에서 5가지만 뽑는 경우의 수를 찾아내는데 18초가 걸렸다.

하지만, memoization으로 성능을 높이면 어떨까?

단 0.001초 만에 계산했다.

그래서 재귀로 작성할 때는 고려할 점이 있다.

<고려할 점>
1. 종료 지점을 작성해야 한다.
재귀에서 종료 지점을 작성하여 (ex. 1일 때 return) 프로그램이 잘 종료되도록 해야 한다.

2. Memoization으로 성능 강화
현재 상태를 저장하고, 다음 재귀에 넘겨주어 성능을 강화할 수 있다.

이렇게 하면 시간 복잡도를 O(N*K)로 만들 수 있다.