정렬
정렬 알고리즘은 주어진 n개의 입력을, 사용자에 기준에 맞게 순차적으로 순서를 매기는 과정이다.
정렬 알고리즘은 여러 가지가 있고, 정렬 방식에 따라 시간 복잡도가 다르다.
대표적으로 선택 정렬, 삽입 정렬, 버블 정렬, 병합 정렬, 힙 정렬, 퀵 정렬이 있다.
그래서 오늘은 이 6가지 정렬 알고리즘에 대해서 알아보도록 하자.
선택 정렬
9 / 6 / 7 / 3 / 5 로 예시를 살펴보자.
선택 정렬은 요소를 삽입 할 위치는 정해져 있고, swap할 요소를 선택하는 알고리즘이다.
오름차순 정렬을 위해서, 최소 값을 찾아서 각 순서에 맞게 swap을 진행한다.
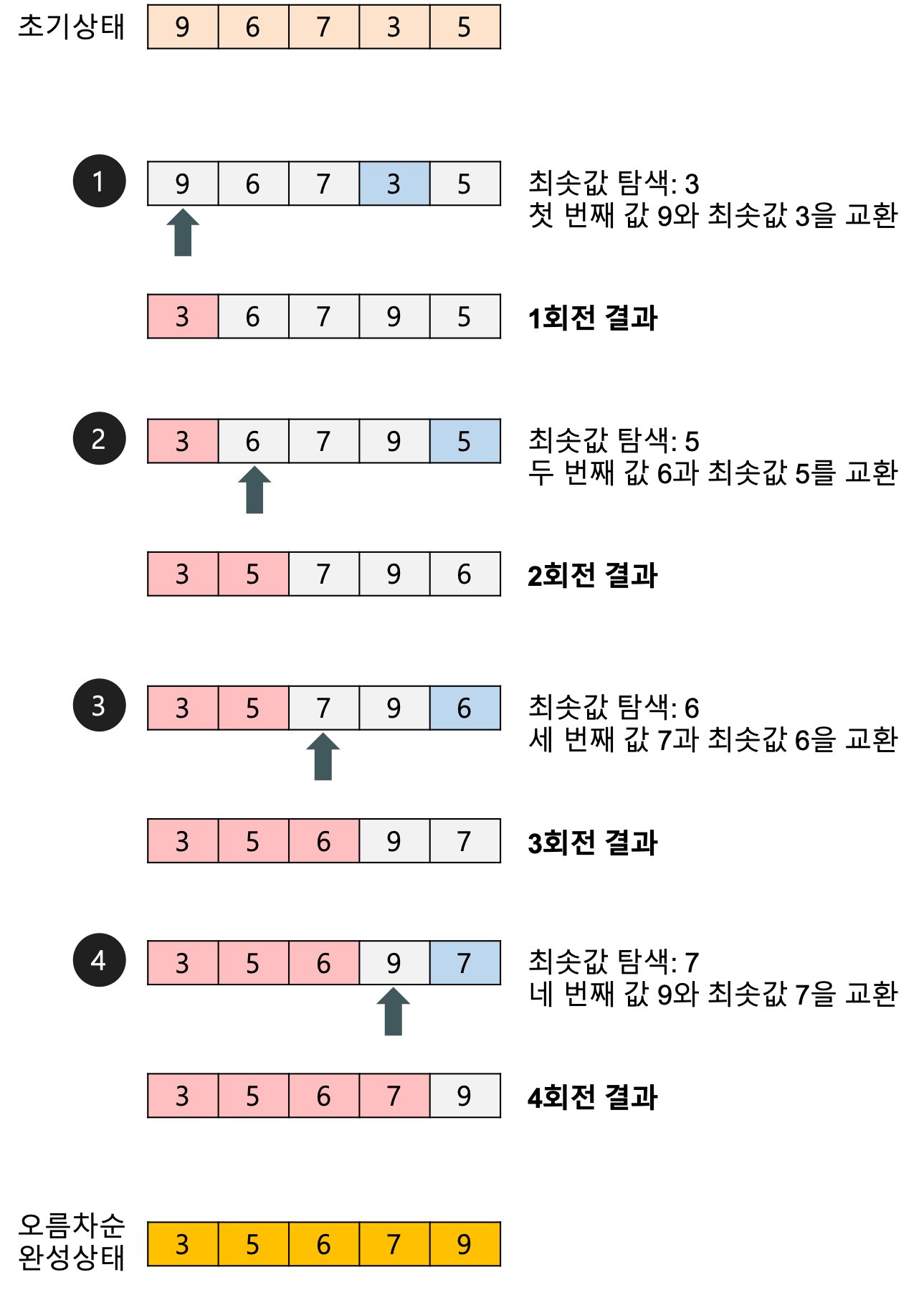
선택 정렬은 어떻게 정렬이 되어있든 상관 없이 계속 반복문을 돌면서,
최소 값을 파악해야하기 때문에 무조건 O(n^2)의 시간 복잡도를 가지는 알고리즘이다.
선택 정렬 구현 코드
## 오름 차순으로 선택 정렬
def select_sort(list):
for i,v in enumerate(list):
min = v
min_index = i
# 최솟 값 찾기
for j in range(i, len(list)):
if list[j] < min:
min = list[j]
min_index = j
list[i], list[min_index] = min, list[i]
print(list)
list = [7,5,9,5,49,38,4,5,2,3]
select_sort(list)삽입 정렬
삽입 정렬은 정렬이 완료된 부분, 정렬이 필요한 부분 그리고, 현재 삽입 할 값 이 세가지로 구분된다.
주황: 정렬이 완료된 부분빨강: 현재 삽입 할 값파랑: 아직 정렬하지 않은 부분
삽입할 값을 정렬 해야 할 부분에서 삽입할 위치를 찾아야 한다.
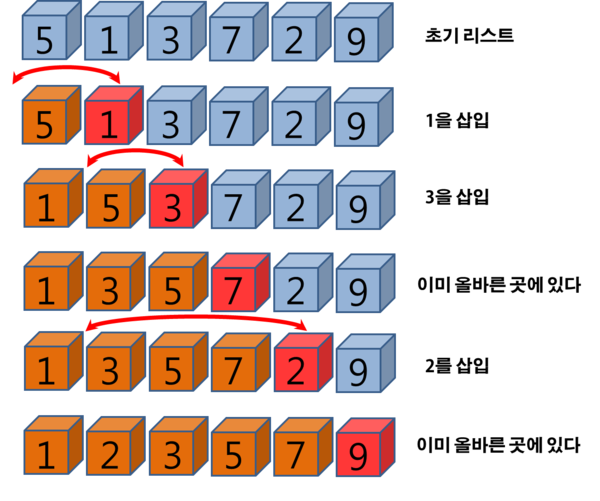
이미 정렬되어 있는 상황, 즉 Best인 상황에서는 O(N)이고,
Worst인 상황에서는 이중 반복문을 돌며 탐색해야하니, O(N^2)이 된다
삽입 정렬 python 코드
def Insertion_sort(list):
sortedList = []
sortedList.append(list.pop(0))
len_list = len(list)
for _ in range(len_list):
print(sortedList)
now = list.pop(0)
now_index = 0
`# 삽입 할 위치 탐색
for j, v_j in enumerate(sortedList):
if v_j <= now:
now_index = j + 1
sortedList.insert(now_index, now)
list = [7,5,9,5,49,38,4,5,2,3]
Insertion_sort(list)실행을 해보면 다음과 같이 결과가 나온다.
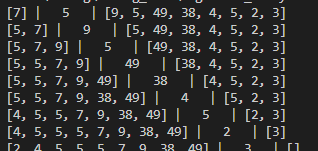
삽입할 값을 sortedList에 삽입하여 정렬을 하는 모습이다.
만약 내림 차순 한다면 삽입 할 위치 조건만 바꿔주면 된다.
버블 정렬
원,투,쓰리,포 버블 버블
잔소린 버블 버블 버블
버블 정렬은 요소를 거품에 태워서 밀어버려서 버블 정렬이라고 한다. 아마도

최댓값을 찾아서, List 끝까지 밀어버리는 과정이라고 생각해보자.
버블 정렬은 하나씩 비교해서 가장 큰 값을 맨 뒤로 밀어버린다.

이 과정을 통해서 주황 부분은 정렬이 완료된 부분이니, 한 사이클을 더 돌면 7이 정렬이 될 것으로 보인다.
python 코드 보기
def bubble_sort(list):
for i in range(len(list)-1):
for j in range(len(list)-i-1):
if list[j] > list[j+1]:
list[j], list[j+1] = list[j+1], list[j]
print(list)
list = [7,5,9,5,49,38,4,5,2,3]
bubble_sort(list)정렬해보면, 최대값 순으로 정렬되는 것을 볼 수 있다.
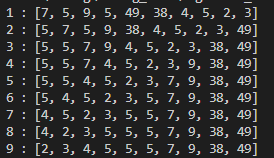
버블 정렬은 무조건 이중 반복문을 따르기 때문에 어떤 상황에 O(n^2) 의 시간 복잡도를 가지고 있다.
병합 정렬
병합 정렬에서 가장 중요한 개념은 Divide & Conquer 이다.
List를 SubList로 나누고, 나눈 SubList에서 정렬을 진행하고, 다시 결합 (Combine)하는 과정을 가진다.
- 병합 정렬은 추가적인 리스트가 필요하다
- 실제적인 정렬은
SubList를 다시 결합 (Combine) 할 때 이루어진다.
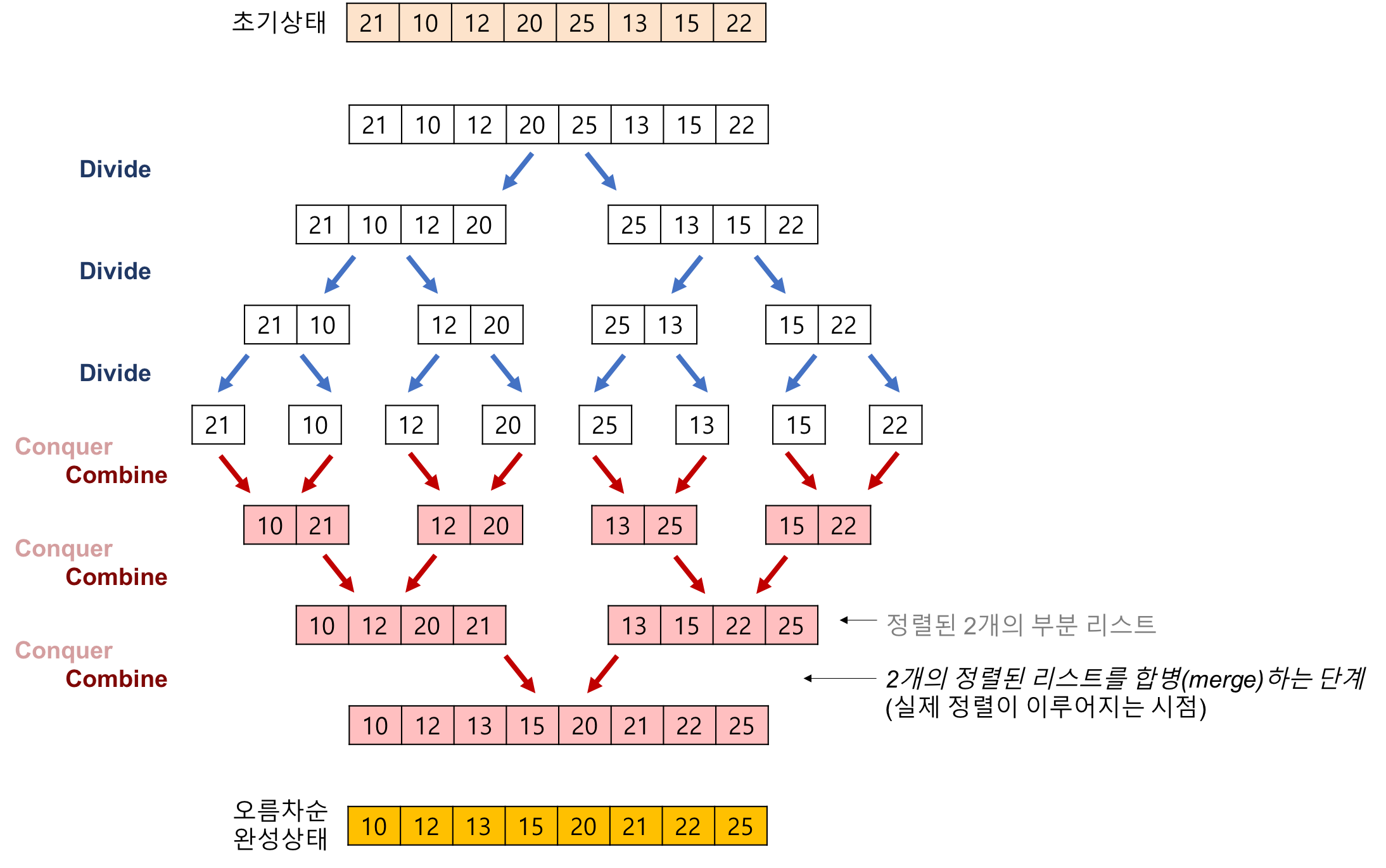
결합할 때, 상세하게 알아보자.
두개의 서브 리스트에서 최소값을 비교하여 정렬된 List에 삽입한다.
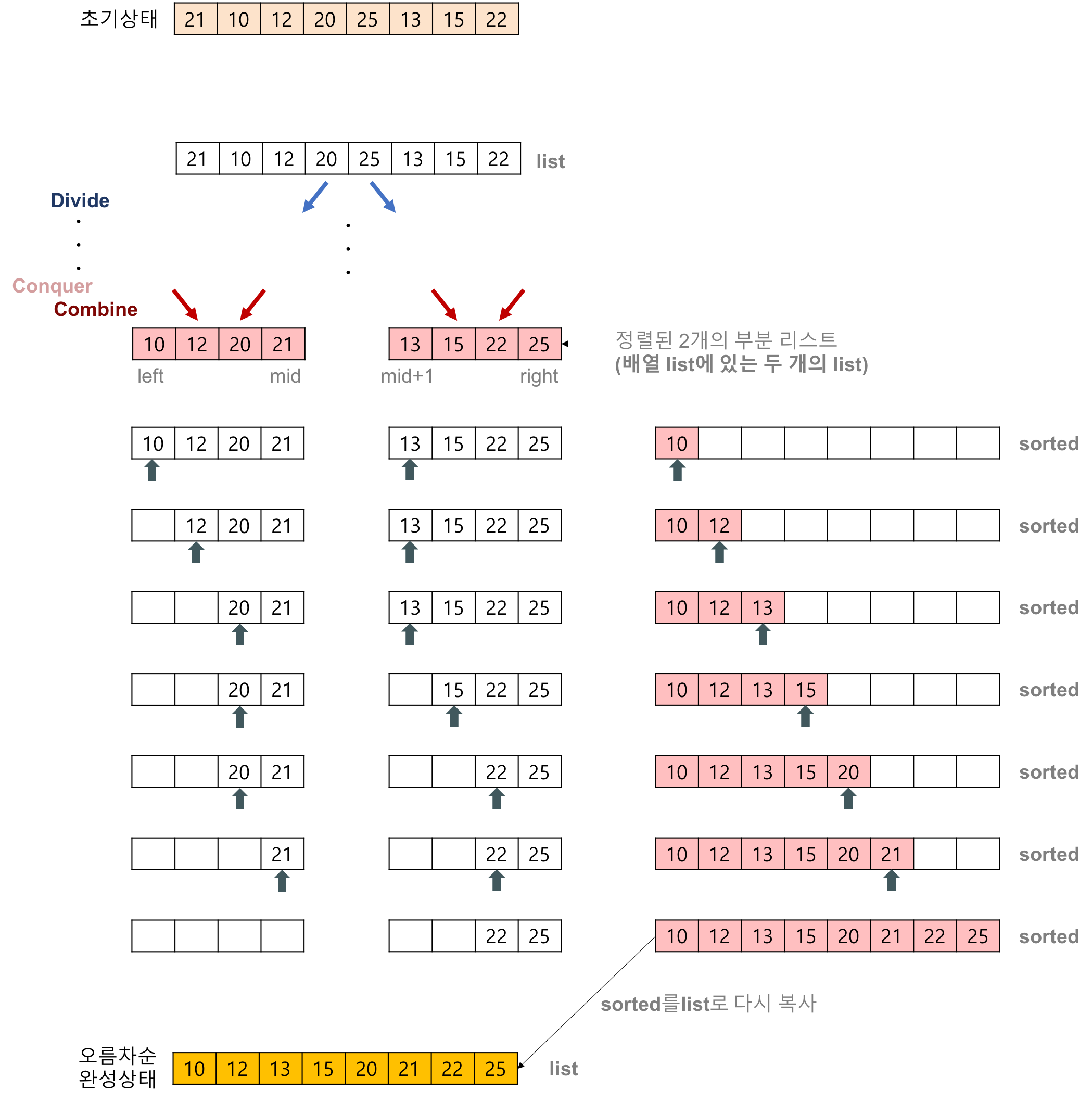
Python 코드
List를SubList두개로 나눔SubList도 재귀 함수인merge_sort함수를 호출하여 정렬을 진행함.- 정렬이 된 두
subList를 최소값들을 비교하여Sorted된 List에 넣음 - 이때 SubList는
pop하고,SubList가 Empty하면 ⭐모든 정렬 완료⭐
def merge_sort(arr):
if len(arr) < 2:
return arr
# SubList 2개로 나누는 과정
mid = len(arr) // 2
low_arr = merge_sort(arr[:mid])
high_arr = merge_sort(arr[mid:])
merged_arr = []
l = h = 0
while l < len(low_arr) and h < len(high_arr):
if low_arr[l] < high_arr[h]:
merged_arr.append(low_arr[l])
l += 1
else:
merged_arr.append(high_arr[h])
h += 1
merged_arr += low_arr[l:]
merged_arr += high_arr[h:]
return merged_arr
list = [7,5,9,5,49,38,4,5,2,3]
print(merge_sort(list))병합 정렬은 어떤 순간에도 O(nlogn)을 제공한다.
그 이유는 T(n) = nlog₂n(비교) + 2nlog₂n(이동) = 3nlog₂n = O(nlog₂n) 이 된다.
퀵 정렬
퀵 정렬도 병합 정렬과 동일하게 Divied and Conquer 방식을 사용한다.
하지만 병합 정렬과 다른 점은 SubList를 사용하지 않고, 기존의 리스트를 활용한다는 점이다.
이러한 측면에서 메모리 사용이 더 적다.
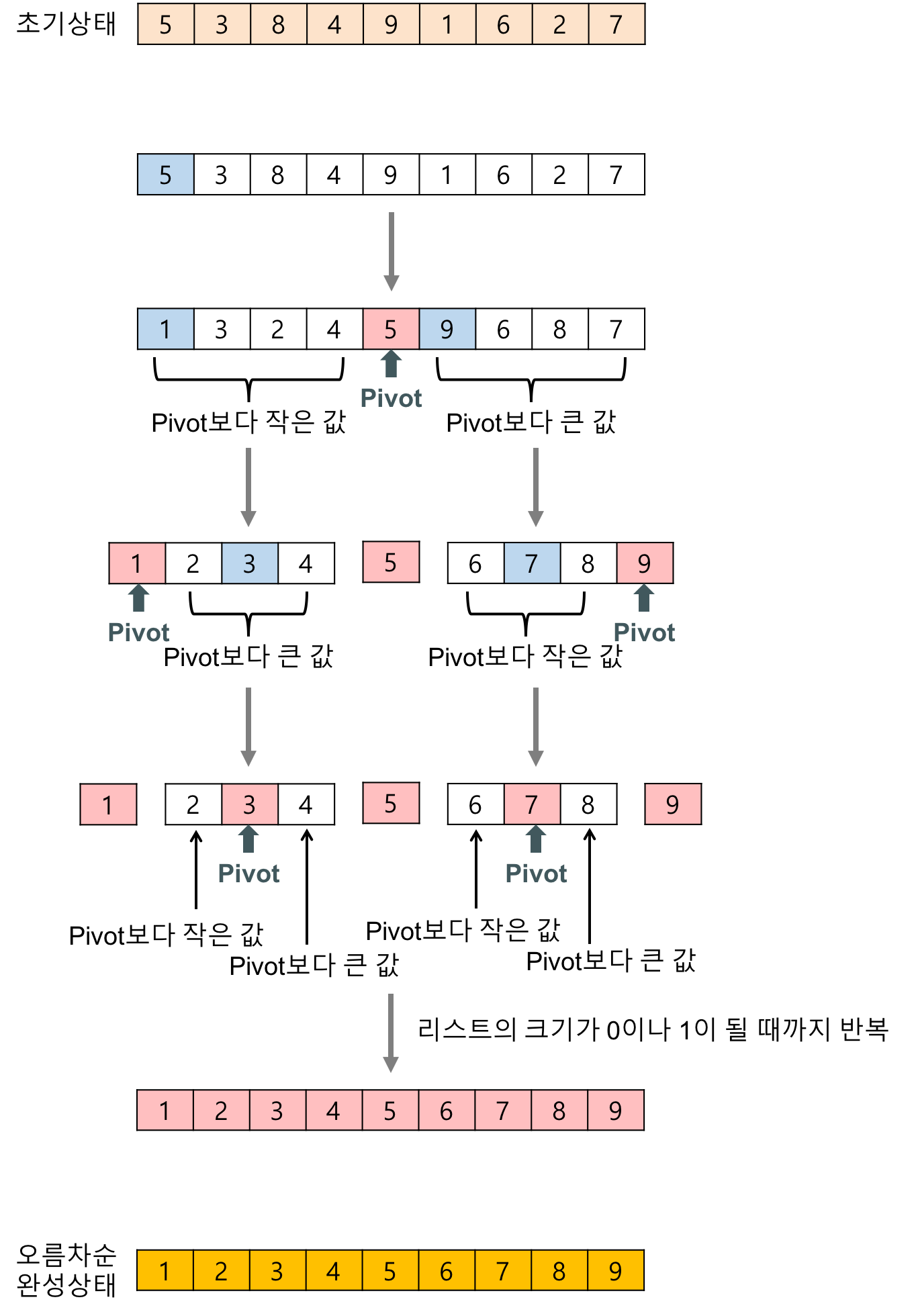
퀵 정렬은 pivot 선정에 따라 시간 복잡도가 달려있다.
가장 Best는 pivot의 중간 값일 때가 가장 좋다.
왜냐하면, Pivot 기준으로 나누었을 때, 한 쪽에 요소가 몰려 있으면,
Divied and Conquer의 퍼포먼스가 잘 나오지 않는다.
그래서 가장 최악은 O(N^2) 까지 될 수도 있다. 하지만 평균은 O(NlogN)이 된다.
파이썬 코드
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
lesser_arr, equal_arr, greater_arr = [], [], []
for num in arr:
if num < pivot:
lesser_arr.append(num)
elif num > pivot:
greater_arr.append(num)
else:
equal_arr.append(num)
return quick_sort(lesser_arr) + equal_arr + quick_sort(greater_arr)힙 정렬
힙 정렬은 Heap의 자료구조를 이용한 정렬이다.
힙에서는 정렬을 위해 삽입과 삭제를 하면 힙의 재구조화 또는 Heapify가 이루어진다.
힙의 재구조화를 통해서 정렬을 하는 방식이다.
사실 Heap 관련해서는 블로그 포스팅을 해두었기 때문에, [자료구조] Heap (힙) 이 글을 참고 부탁드립니다.
비교
| 최고 | 평균 | 최악 | |
|---|---|---|---|
| 선택 정렬 | O(n^2) | O(n^2) | O(n^2) |
| 삽입 정렬 | O(n) | O(n^2) | O(n^2) |
| 버블 정렬 | O(n^2) | O(n^2) | O(n^2) |
| 병합 정렬 | O(nlogn) | O(nlogn) | O(nlogn) |
| 퀵 정렬 | O(nlogn) | O(nlogn) | O(n^2) |
| 힙 정렬 | O(nlogn) | O(nlogn) | O(nlogn) |
