[자료구조] Heap (힙)

우선순위 큐

힙을 이해하기 위해서는 우선순위 큐를 이해 해야 한다.

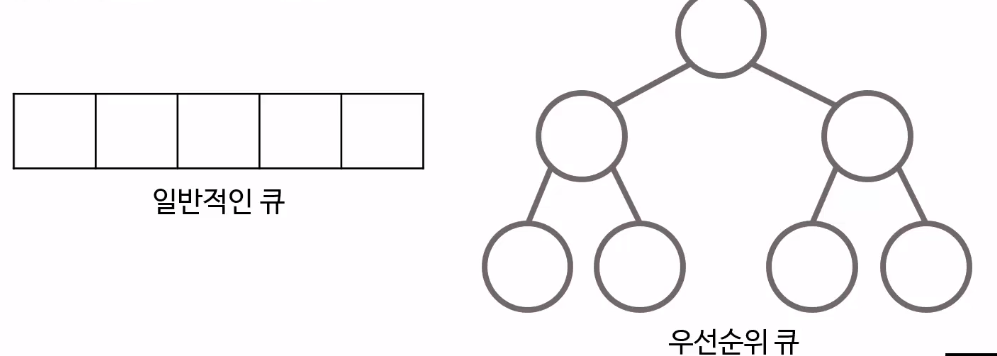
일단 큐는 FIFO로 동작한다. First In First Out 먼저 들어온 요소가 먼저 나온다.

• 우선순위 큐는 큐에 우선순위를 접목시킨 개념이다.
• 우선순위 큐에서 우선순위가 높은 데이터 먼저 나가는 형태이다.

그래서 큐는 선형적인 구조이지만, 우선순위 큐는 Tree의 형태로 되어있다.

힙 (Heap)

• 우선순위 큐를 위해 고안된 완전이진트리 형태의 자료구조

• 여러 값 중, 최대값과 최소값을 빠르게 찾아내도록 만들어진 자료구조

• 반정렬 상태를 유지
  ex. 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큼 / 작음

• 이진탐색트리(BST)와 달리 중복된 값이 허용된다.

• 삽입과 삭제 모두 O(logN)의 시간 복잡도를 가지고 있다. 그 이유는 삽입과 삭제 연산이 일어날 때마다, 힙의 재구조화 (heapify) 작업이 일어나기 때문이다.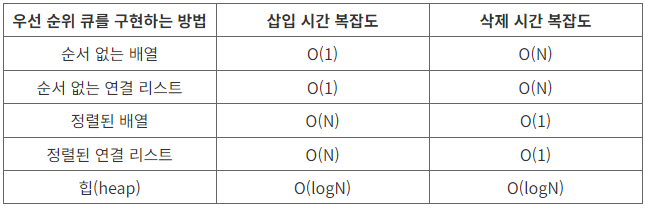

힙의 종류

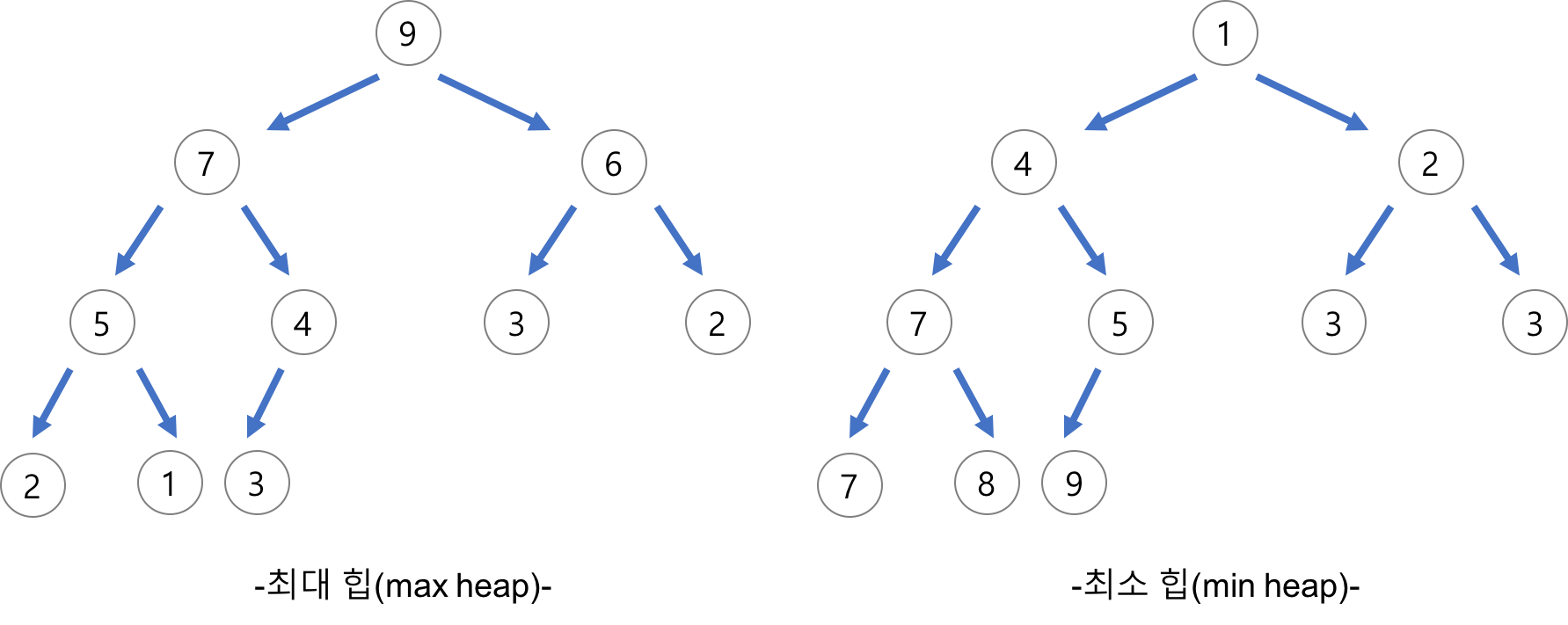
1. 최대 힙 (max heap)

• 부모 노드의 키값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
• key(부모 노드) >= key(자식 노드)

2. 최소 힙 (min heap)

• 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
• key(부모 노드) <= key(자식 노드)
  
  
  

Heapify 힙의 재구조화

힙에서 삽입과 삭제 연산을 할 때마다, heapify 연산이 일어난다. 그냥 Tree대로 삽입과 삭제를 한다면 힙의 구조가 깨질 수 있다.

최소 힙에 삽입과 삭제 과정을 거치며 heapify를 알아보자.

<삽입 연산>

1. 일단 우선순위가 낮다고 가정하고 이진 Tree에 삽입하는 순서대로 삽입한다.
   

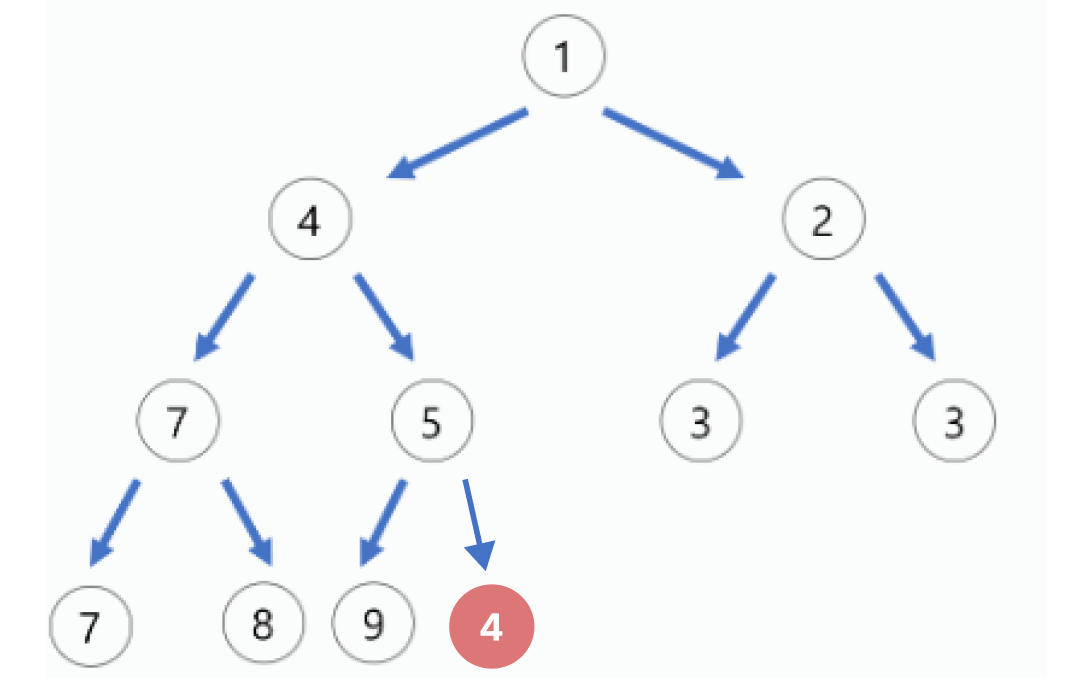
2. 삽입한 노드와 그의 부모 노드를 비교를 진행한다.
   최소 힙이므로, 키 값이 작은 노드가 부모 노드로 가야하므로 두개를 Swap한다.
   

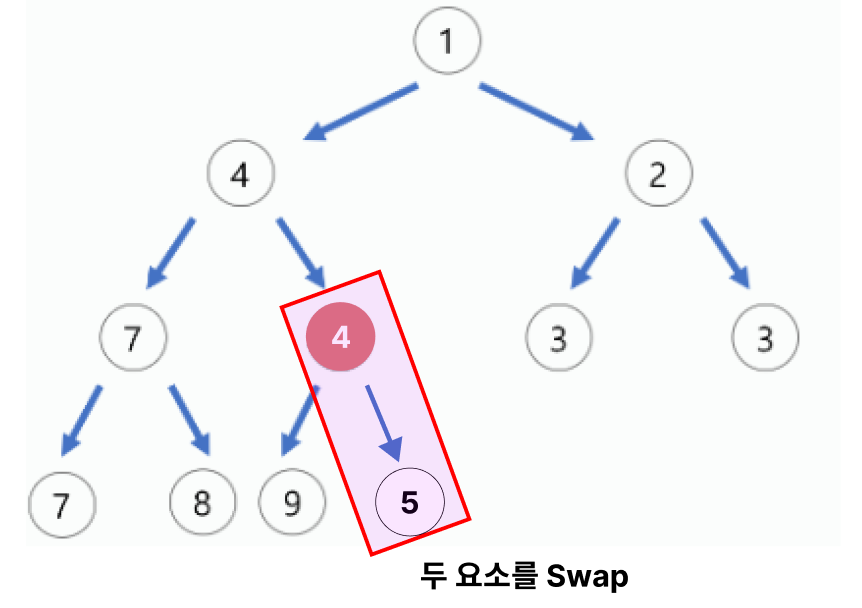
3. 계속해서 부모노드와 비교한다.하지만 값이 동일하거나, 대상 노드가 값이 더 크면 그만한다.
   

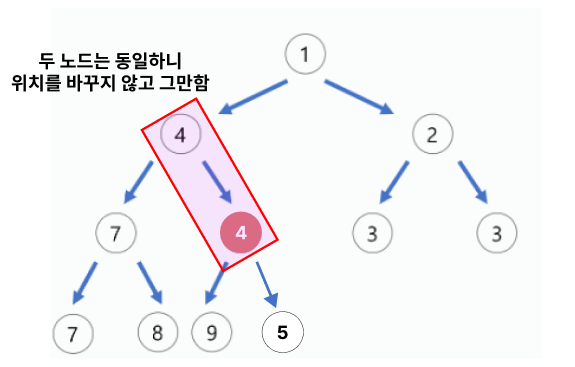
<삭제 연산>
1. Heap에서 pop하면 부모 노드를 출력한다.

2. 마지막 노드를 Root 노드로 이동 시킨다.
   

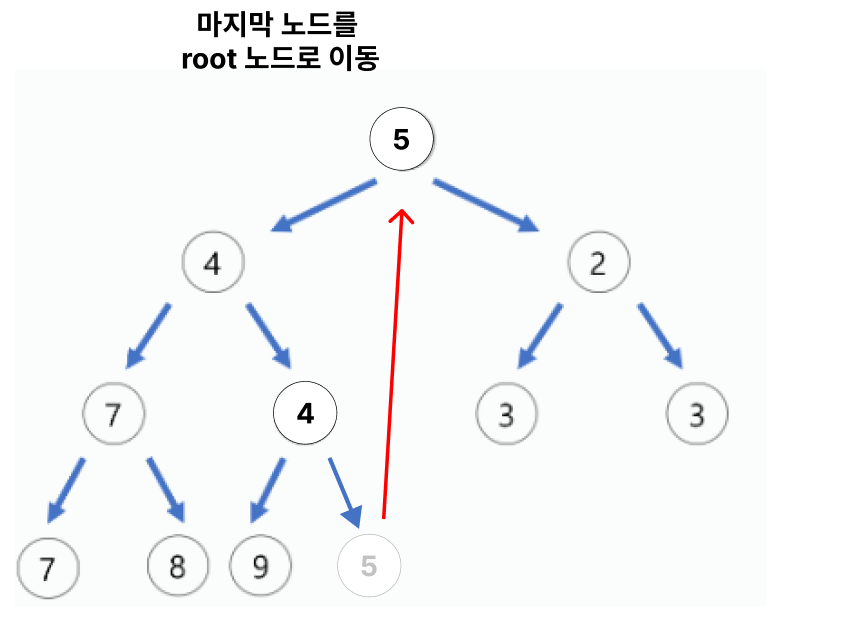
3. 양 옆 노드와 값을 비교하여, 더 작은 값을 Root 노드로 이동 시킨다.
   

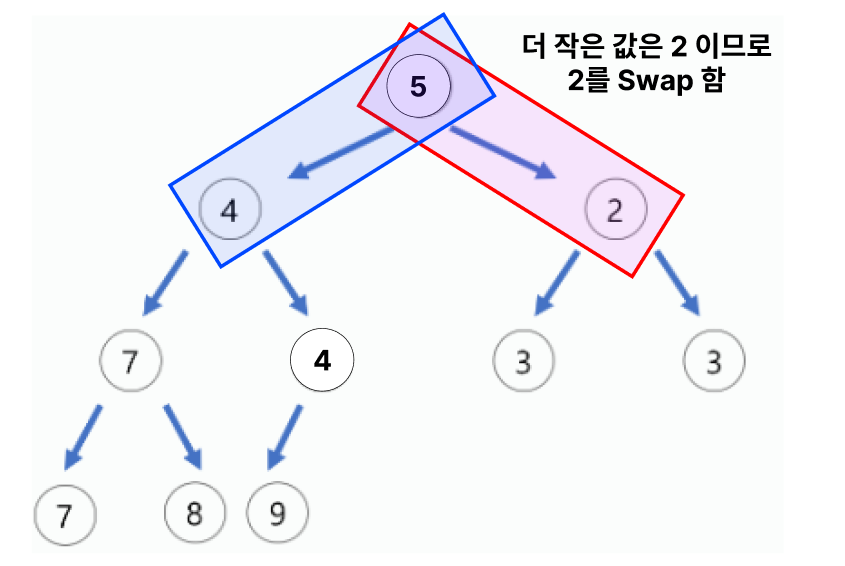
4. 계속해서 값을 또 비교한다. 비교할 값이 더 크면 계속해서 자식 노드로 내린다.
   

5. 마무리
   

Python heapq

Python에서는 힙을 위해 heapq 라이브러리를 제공한다. heapq 외에도 PriorityQueue 라이브러리도 제공하고 있지만, 코딩 테스트 환경에서는 보통 heapq가 더 빠르게 동작한다.

heapq는 최소 힙만 제공한다. 단순히 원소를 힙에 전부 넣었다가 빼는 것만으로 오름차순 정렬이 완료되고, O(NlogN)의 시간복잡도를 가진다. *참고 : List 정렬 메소드도 O(NlogN)

import heapq

def heapsort(iterable):
	h = []
	result = []
    #모든 원소를 차례대로 힙에 삽입
    for value in iterable:
    	heapq.heappush(h, value)
        
    # 힙에 삽입된 모든 노드를 차례대로 꺼내기
    for _ in range(len(h)):
    	result.append(heapq.heappop(h))
    return result

만약 내림차순 정렬을 위해 최대 힙을 사용하고 싶다면, 파이썬 라이브러리는 최대 힙을 제공하지 않으므로, 힙에 넣을 때 부호를 바꾸어 넣고, pop할 때 다시 부호를 바꾸면 내림차순으로 최대 힙 정렬를 할 수 있다.