[자료구조] 그래프

그래프란?

노드(N, node)와 그 노드를 연결하는 간선(E, edge)를 하나로 모아 놓은 자료구조.
➜ 즉, 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료 구조.

그래프를 이야기하면 트리와의 차이를 보아야 한다.


<그래프와 트리의 차이>

• 정의
  • 그래프 : 노드(N, node)와 그 노드를 연결하는 간선(E, edge)를 하나로 모아 놓음       ➜ 방향, 무방향 모두 존재
  • 트리 : 그래프의 한 종류, 방향성이 있는 비순환 그래프
    
    
• 사이클
  • 그래프 : 사이클 가능, 자체 간선 가능, 순환 그래프, 비순환 그래프 모두 존재
  • 트리 : 사이크, 자체 간선 모두 불가능, 비순환 그래프만 존재
    
    
• 노드와 부모와 자식
  • 그래프 : 루트 개념이 없고, 부모-자식의 개념이 없음
  • 트리 : 루트 개념이 존재하고, 부모-자식의 개념이 존재함

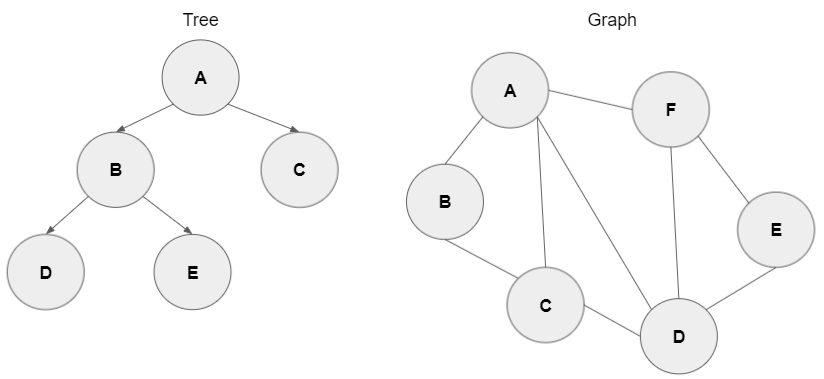
트리와, 그래프의 차이 중 가장 큰 것은 순환의 여부를 파악하면 된다.
순환이 가능하면 그래프, 순환이 불가능하면 트리

물론, 그래프도 비순환 그래프도 존재한다. 즉, 트리도 그래프의 한 부분이라고 볼 수 있다.

그래프와 관련된 용어

• 정점 (vertex, node) : 하나의 위치
• 간선 (edge) : 위치 간의 관계. 노드를 연결하는 선
• 인접 정점 (adjacent vertex) : 간선에 의해 직접 연결된 정점
• 차수 (degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
• 사이클 : 단순 경로의 시작 정점과 종료 정점이 동일한 경우
• 오일러 경로 : 그래프에 존재하는 모든 간선을 한 번씩만 통과하면서, 처음 정점으로 되돌아오는 경로를 말함. 간선의 개수가 짝수일 때만 가능!

그래프의 종류

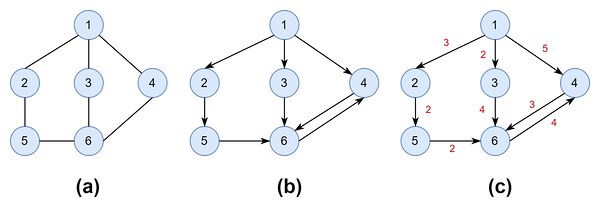
(a) 무방향 그래프

• 방향성이 없는 그래프, 간선을 통해서 양 방향으로 갈 수 있다.
• Vertex A 와 Vertex B 를 연결하는 간선은 (A,B)로 표기

(b) 방향 그래프

• 방향성이 존재하는 그래프, 간선을 통해서 한 방향으로만 갈 수 있음.
• A → B로 갈 수 있는 간선은 <A, B>로 표기

(c) 가중 그래프

• 그래프 간선에 가중치를 부여한 그래프.
• 가중치는 한 지점에서 다른 지점으로 이동하는 데 필요한 비용이나 걸리는 시간

사이클 vs 비순환 그래프

• 사이클 : 경로에서 시작 정점과 종료 정점이 동일한 경우
• 비순환 그래프 (트리) : 사이클이 없는 그래프

완전 그래프

• 모든 정점이 서로 연결되어 있는 그래프
• 정점 수 : n이면, 간선의 수 : n * (n-1) / 2

Python에서 그래프를 구현하는 방법

1. 인접 행렬

• 그래프의 연결 관계를 행렬로 표현하여, 이차원 배열로 나타내는 방식

adj[i][j] : 노드 i에서 j로 가는 간선이 존재할 경우 1, 아니면 0
만약 가중치 그래프라면, 1대신 가중치를 넣으면 된다

무방향 그래프 라면, i → j / j → i 둘 다 가능하므로, 행렬이 대칭을 이룰 것이다.

노드의 개수, 간선의 개수, 연결 정보가 주어진다면

4 5 # 노드의 개수, 간선의 개수
1 2 # 연결 정보
2 3 
1 4
1 3

from sys import stdin

node, edge = map(int, stdin.readline().split())

adj = [[0 for _ in range(node+1) for _ in range(node+1)]

for _ in range(edge):
    src, dest = map(int, stdin.readline().split())
    adj[src][dest] = 1
    adj[dest][src] = 1

2. 인접 리스트

파이썬의 리스트에서 append을 통해서 구현이 가능하다.

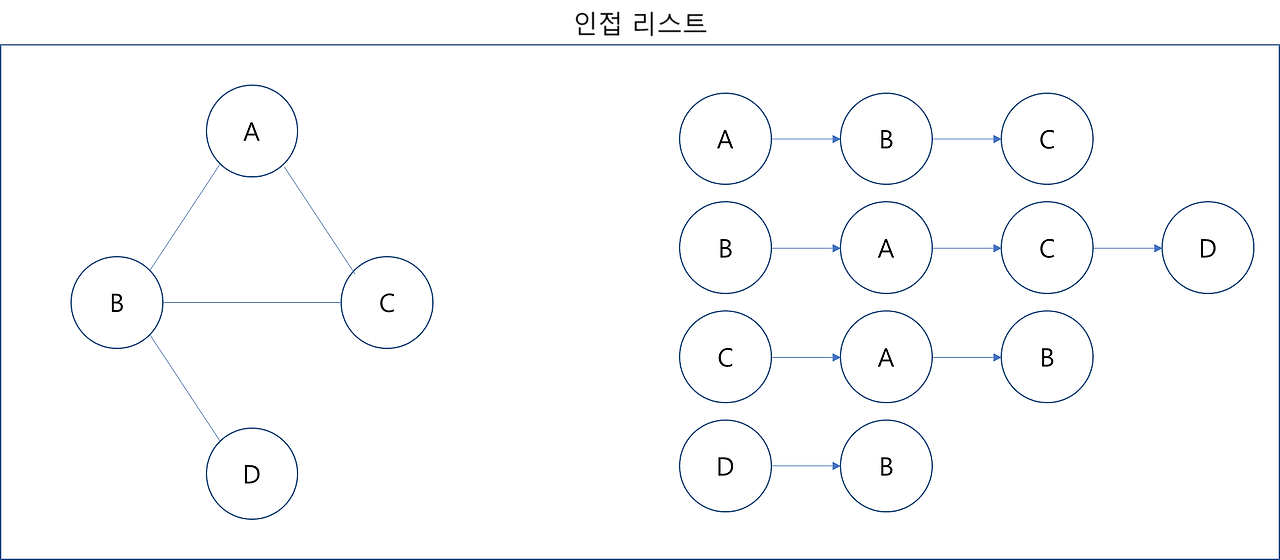
이중 리스트에 연결되어 있는 노드를 기록하는 방식이다.

노드의 개수, 간선의 개수, 연결 정보가 주어진다면

4 5 # 노드의 개수, 간선의 개수
1 2 # 연결 정보
2 3 
1 4
1 3

from sys import stdin

node, edge = map(int, stdin.readline().split())

adj = [ [] for _ in range(node+1)]

for _ in range(edge):
    src, dest = map(int, stdin.readline().split())
    adj[src].append(dest)
    adj[dest].append(src)

adj = [["B", "C"], ["A", "C", "D"], ["A", "B"], ["B"]]

비교

이제 두 코드의 시간 복잡도를 비교해보겠습니다:

1. 인접 행렬을 사용한 두 번째 코드의 시간 복잡도: O(node^2 + edge)
2. 인접 리스트를 사용한 첫 번째 코드의 시간 복잡도: O(node + edge)

일반적으로, 노드 수 node가 많고 간선 수 edge가 적을 경우, 인접 리스트를 사용하는 첫 번째 코드가 더 효율적입니다. 반면에, 노드 수 node가 적고 간선 수 edge가 많은 경우, 인접 행렬을 사용하는 두 번째 코드가 더 효율적일 수 있습니다.