에라토스테네스의 체

에라토스테네스의 체

그리스 수학자인 에라토스테네스가 고안한 소수를 찾는 방법.

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
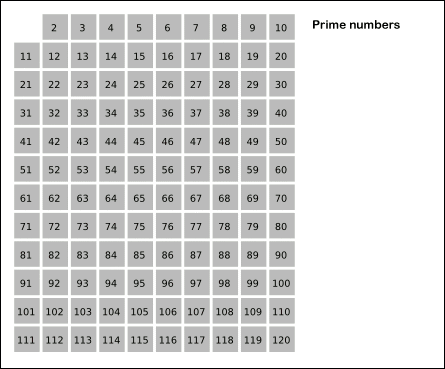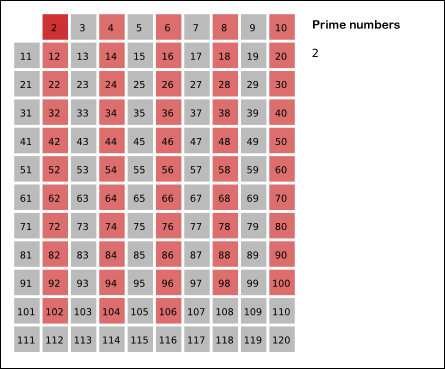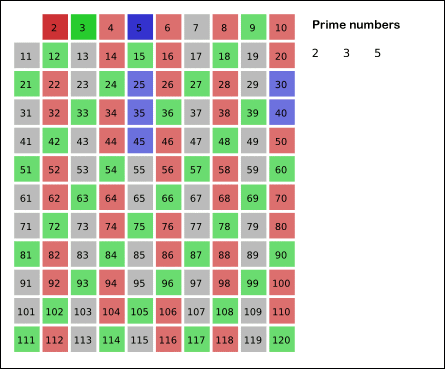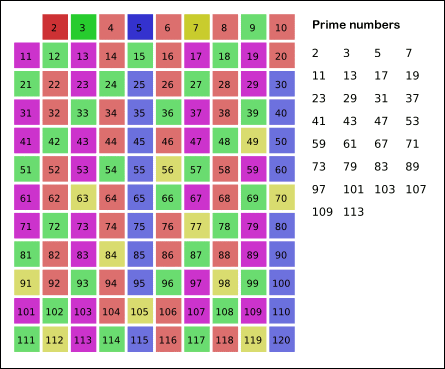
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다. (보라색)

그림의 경우, 112>120 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

Java로 구현

List<Boolean> primeList = new ArrayList<>;

Boolean값을 가지는 primeList 생성
소수면 true, 아니면 false 값을 가지도록 할 것임.

primeList.add(false);
primeList.add(false);

0과 1은 소수가 아니기에 먼저 false값 넣어줌.

for (int i = 2; i <= n; i++) {
	primeList.add(i, true);
}

2부터 n까지는 true로 초기화 해줌.

for (int i = 2; i <= Math.sqrt(n); i++) {
	if(primeList.get(i)) {
		for (int j = i * i; j <= n ; j += i) {
			primeList.set(j, false);
		}
	}	
}

i가 2부터 시작해 n의 제곱근까지만 반복
만약 i 인덱스의 값이 true라면 i를 제외한 i의 배수 인덱스 값을 false로 설정.