출처[LECTURE16]
강의 영상 및 자료:
https://mhsung.github.io/kaist-cs492d-fall-2024/
해당 강의를 기반으로 추가적인 설명을 정리했습니다. 해당 강의에서 수식적인 부분이 많아서 최대한 큰 흐름을 이해할 수 있는 내용들을 위주로 정리했습니다.

Flow Matching

이전 강의에서 배웠던 Conditional probability paths, flow map, vector field에 관한 수식입니다.

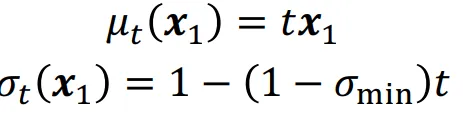
만약 평균과 분산이 위에처럼 주어졌을 때 위의 3가지 수식이 어떻게 나타나는지를 퀴즈로 내주셨습니다. 갑자기 뜬금없이 위의 수식이 나와서 생각해보니 평균의 경우 초기 $x_1$으로부터 시간에 따라 선형적으로 데이터를 표현하고, 분산의 경우도 마찬가지로 t=0일 때는 1, 1일때는 매우 작은 분산인 $\sigma_{min}$을 선형적으로 보여주는 값입니다.

어쨌든 위의 평균과 분산을 대입한 결과는 위의 그림처럼 나오고, 여기서 $\sigma_{min}$은 매우 작은 값이기 때문에 이를 0으로 보낼 경우

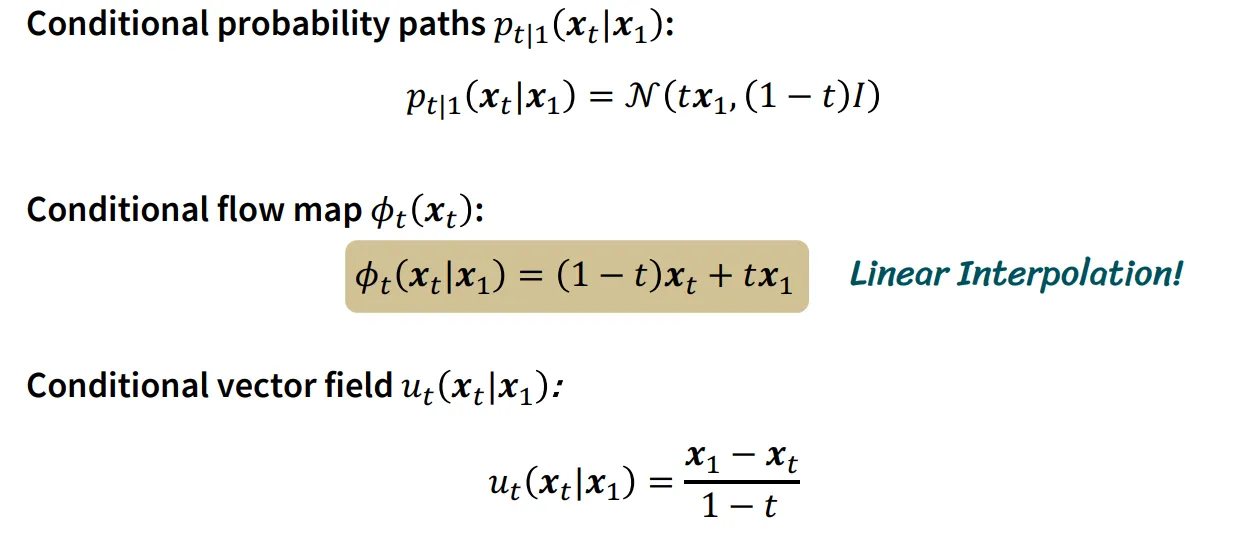
처음에 가정했던 linear interpolation으로 표현된 수식이 완성됩니다.

Linear interpolation으로 설계된 flow matching의 경우 데이터 샘플 $x_1$을 얻고, 거기에 가우시안 분포에서 $x_0$까지 얻으면, linear하게 설계된 $\phi_t(x_0|x_1)$를 계산합니다. 이후 vector field도 간단하게 구한다음에 neural network로 loss function을 진행하면서 학습하게됩니다.

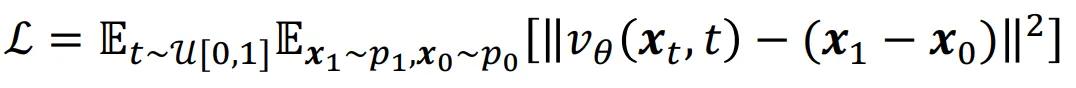
모델자체가 linear하게 설계되어서 매우 쉬운 형태로 나타날 수 있습니다. 사실 수식자체만 보면 diffusion 모델에서 노이즈를 예측하는 형태랑 비슷하게 생겼지만, diffusion 모델과는 다르게 $x_0$의 값을 사용해서 2개의 값이 어떻게 매칭되는지를 알아본다는 점에서 $x_1$에서 추가된 노이즈만 예측하는 diffusion 모델과는 다릅니다.

Rectified Flow

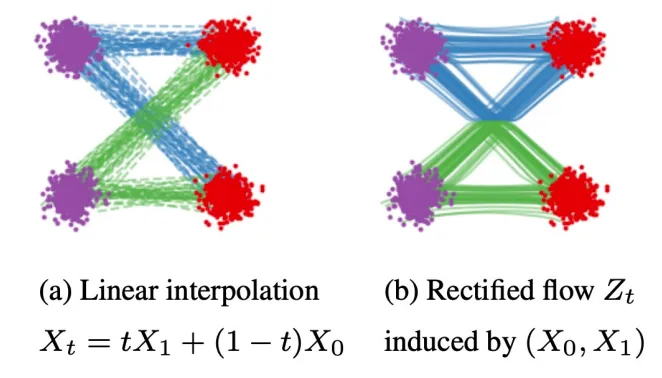
그래서 위에서 제시한 Flow matching의 결과가 좋을까요? 결론만 말하면 “네!”라고 답할 수 있습니다. 하지만 흥미로운 점은 결과를 보면 경로들이 서로 엇갈리는 결과들이 나왔습니다. 보라색에서 빨간색으로 데이터의 분포를 바꿀 때 파란색 경로와 초록색 경로들이 겹치는 것을 확인할 수 있습니다.

이러한 현상을 막기위해서 Rectified flow라는 새로운 방법이 제시됐습니다.

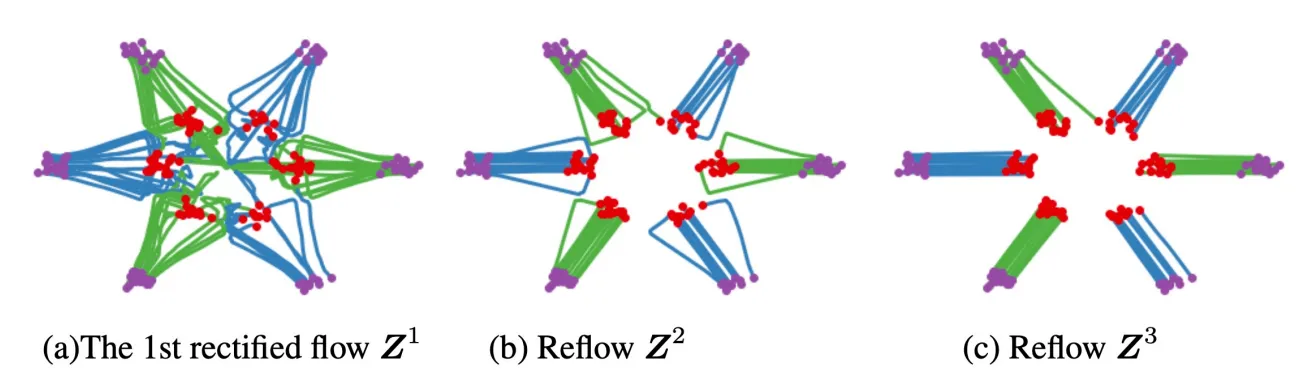
핵심 개념은 rectified flow를 반복하는 것입니다. 첫번째 진행했을 때 왼쪽에 보이는 것처럼 겹치는 부분이 발생했습니다. 하지만 반복할수록 겹치는 부분이 줄고 직선 형태로 생성되는 것을 확인할 수 있습니다.

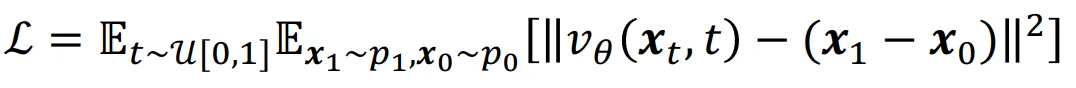
왜 반복할수록 직선성이 강해질까요? 수식을 다시 자세히 보시면 수식 자체가 straightness를 측정합니다. loss가 작아질려면 점점 linear 해져야하기 때문입니다. 따라서 rectified를 반복할수록 직선성이 강해지는 것을 확인할 수 있습니다.

결과를 보면 확실히 많이 진행할수록 성능이 더 좋아지는 것을 확인할 수 있습니다.

InstaFlow

Reflow를 반복할수록 성능이 좋아지는 개념을 diffusion에도 적용할 수 있고, 이를 실제로 구현한 논문이 InstaFlow입니다. 초기에 데이터 분포를 모델을 학습하고 이 결과의 데이터 쌍의 linear interpolation을 사용하여 새로운 Flow 모델의 경로를 재조정(Reflow) 하는 과정을 반복합니다.

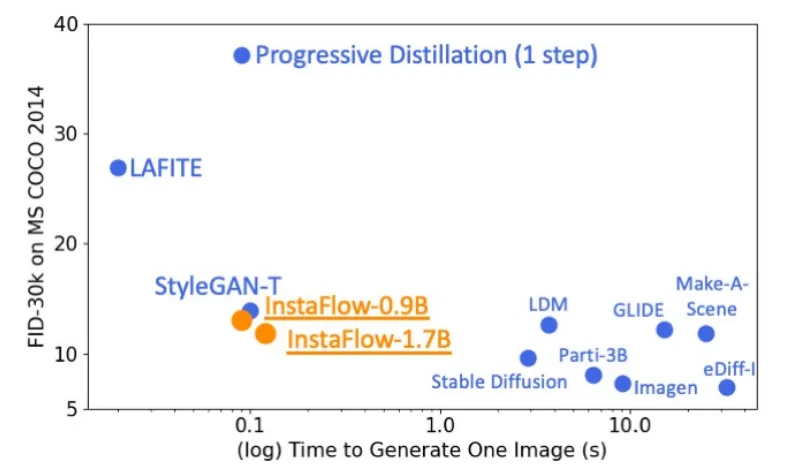
결론적으로 더 적은시간에 더 좋은 결과를 얻을 수 있게 됐습니다. 더 적은 시간을 사용한 이유는 이전 논문들에서 나왔는데, 경로가 더 직선화 될수록 더 적은 스텝으로도 목표에 더 빠르게 도달할 수 있기 때문입니다.