출처[LECTURE15]
강의 영상 및 자료:
https://mhsung.github.io/kaist-cs492d-fall-2024
해당 강의를 기반으로 추가적인 설명을 정리했습니다. 해당 강의에서 수식적인 부분이 많아서 최대한 큰 흐름을 이해할 수 있는 내용들을 위주로 정리했습니다.
Flow matching

Diffusion 모델은 T시점에 간단한 가우시안 분포에서 시작해서 0시점의 복잡한 데이터의 분포를 얻는 것을 목표로 합니다. Flow Matching도 동일하게 작동하지만 T가 0으로 바뀌고, 0이 1로 바뀐다는 차이점이 존재합니다.
Normalizing Flow
하나의 데이터 분포를 다른 데이터 분포로 변환시켜주는 것이 Normalizing Flow입니다. 을 가우시안 분포와 같은 reference distribution, 을 normalizing flow에 의해서 생성되는 새로운 분포라고 했을 때 과 그 역함수 모두 continously differentiable function인 경우 아래와 같은 식이 성립합니다.
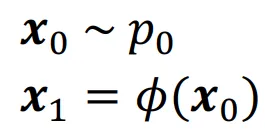
Change of variable
Change-of-variable은 주어진 문제를 더 쉽게 풀기 위해 변수나 좌표계를 새로운 변수로 변환하는 수학적 기법입니다.
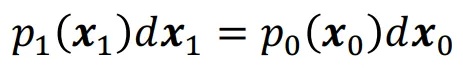
변환될 때 확률 보존의 법칙은 위의 수식처럼 성립해야합니다. 즉 변환되기 이전이나 이후 모두 동일한 확률 질량을 가져야 하는 것 입니다.
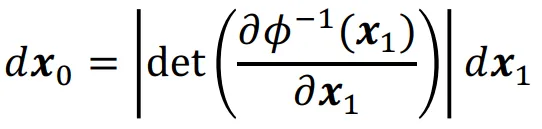
또한 변환할 때 Jacobian determinant를 사용해서 |det()|의 값이 1보다 크면 공간이 늘어나고, 1보다 작으면 공간이 줄어드는 local scali;ng 변화를 확인할 수 있습니다.
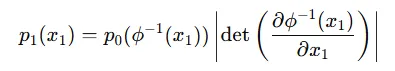
Jacobian matrix를 위와 같이 p로 다시 나타낼 수 있는데, 이때 나타나는 determinant를 push-forward로 간단하게 나타내면 아래와 같습니다.
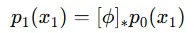
위의 과정을 진행할 때 크게 2개의 고려해야할 사항이 있습니다.
첫번째로 어떻게 역함수를 학습하고 계산할 수 있는가와 두번째로 Jacobian은 어떻게 계산하는지에 대한 부분입니다.
Residual Flow
Function 를 여러개의 함수의 구성요소라고 봅니다.

그리고 각각의 요소는 아래와 같이 정의됩니다.
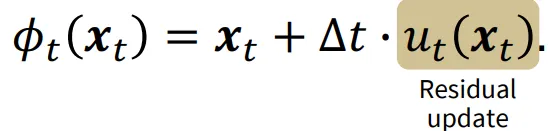
T → , →0으로 간다면 위의 Residual Flow는 ODE 공식과 유사하게 작동할 것입니다. 직관적으로 시간을 무한대로 늘리고, 간격을 0에 가깝게 수렴하면 연속적으로 변하게 될 것입니다.
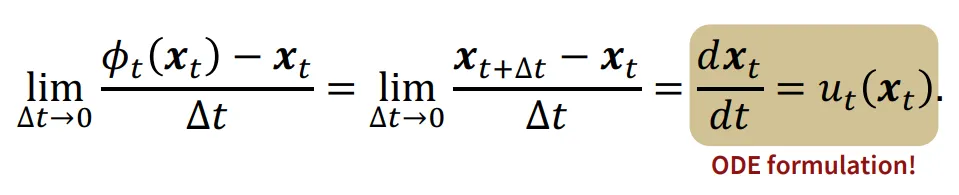
따라서 데이터의 분포를 변화할 때 ODE 형태의 식으로 작성할 수 있게 됐습니다.
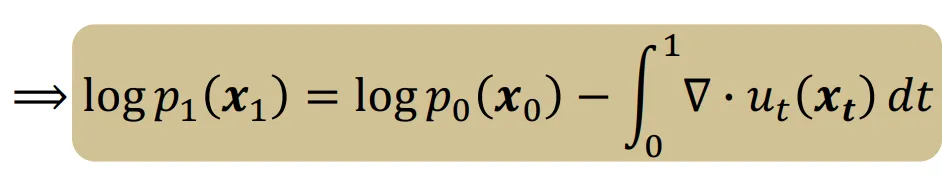
따라서 이전에는 함수에 대해서 학습을 했어야 했는데, 이제는 새로운 vector field라는 를 학습하면 됩니다. Vector field는 공간의 각 점에서 벡터를 할당하는 함수입니다.
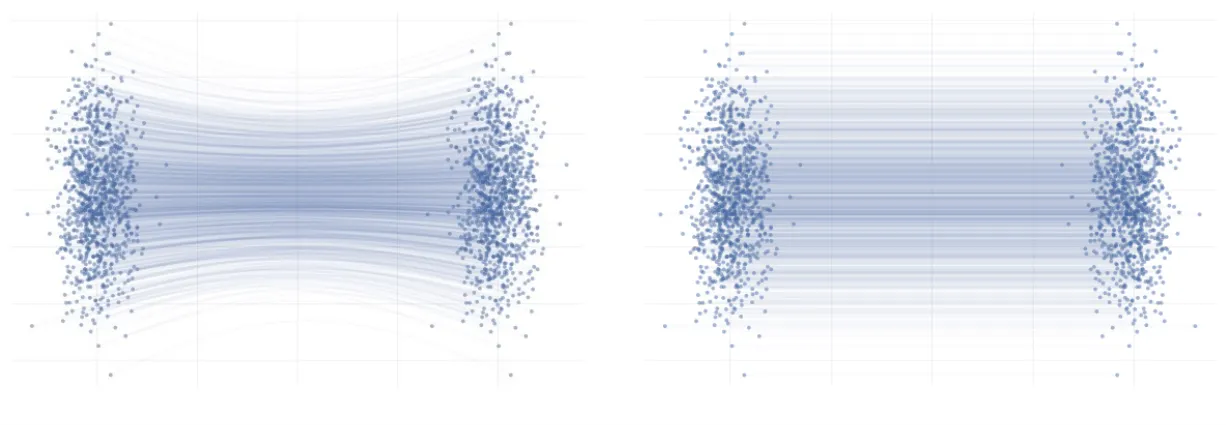
하나의 점에서 다른 점으로의 변환을 나타내는 Vector field는 위의 그림처럼 여러개의 형태로 나타납니다.
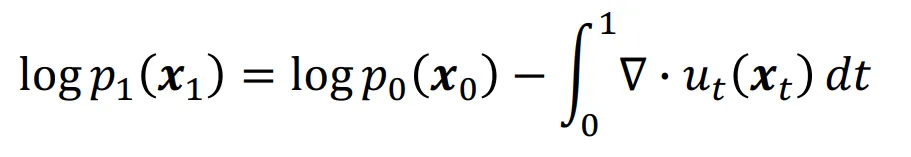
만약 우리가 vector field 를 정확히 알고 있다면 위의 수식이 성립할 것입니다.
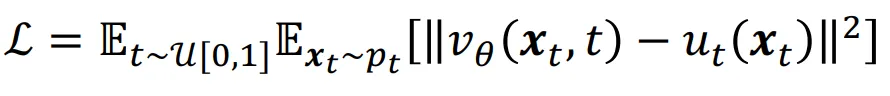
그리고 우리가 학습시키고자 하는 neural network 는 vector field와 유사해지도록 학습될 것입니다. 하지만 우리는 vector field를 알지 못합니다… 그렇다면 어떻게 vector field를 구할 수 있을까요? 바로 아래에서 설명할 conditional probability paths를 이용하는 방법입니다.
Codnitional Probability Paths
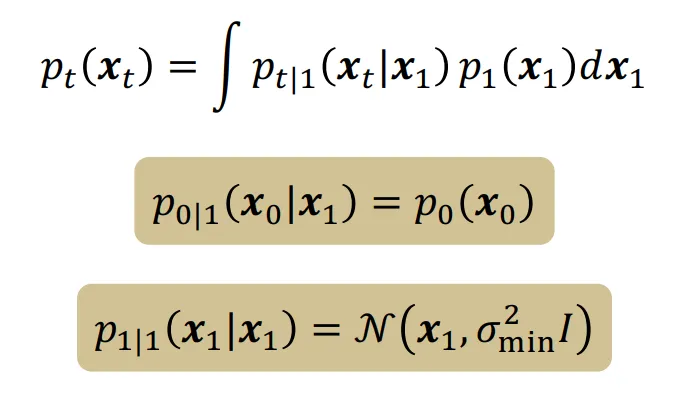
우리는 vector field를 알지 못하기 때문에 Conditional Probability paths라는 개념을 도입하여 특정 데이터 분포를 학습시키고자 합니다. 위의 보이는 식에서는 첫번째 데이터에 관한 path를 구하고 이를 update 하는 과정을 나타낸 것입니다.
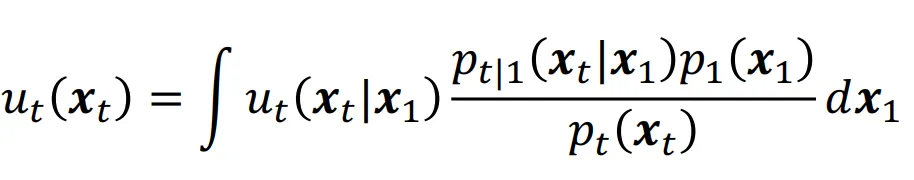
위에서 첫번째 데이터에 대해서 나타낸 값을 모든 데이터에 대해서 구해야 하므로 적분 식을 통해서 모든 데이터들의 값, 즉 marginal vector field를 위와 같이 나타낼 수 있습니다.
하지만 위에 나오는 것처럼 모든 데이터들에 대해서 계산을 하려면 계산량이 너무 많기 때문에 저자는 이를 단순화 할 방법을 찾았습니다.
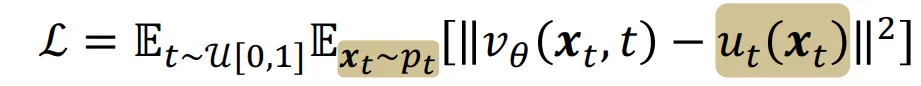
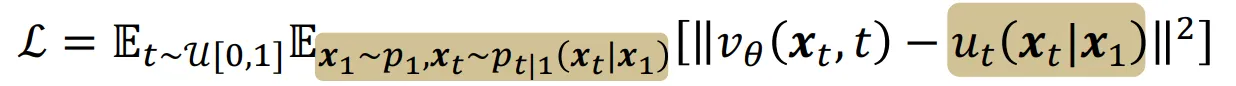
그리고 첫번째 수식과 두번째 수식이 같음, 즉 모든 데이터들의 평균을 학습하는 것과, 부분적인 데이터를 학습하는 것이 결론적으로 같다는 것을 확인했습니다. 따라서 계산은 더욱 간단해 질 것입니다.
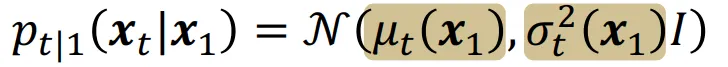
선택한 데이터의 분포는 정규분포가 되도록 설정했습니다.
