출처[LECTURE02]

강의 영상: https://www.youtube.com/watch?v=Nh9MIEbCJIw

해당 강의를 기반으로 추가적인 코드 구현과 설명을 정리했습니다.

Variational Autoencoder(VAE)

Marginal Distribution(주변 분포)

정의: 여러 확률 변수들로 구성된 확률 분포에서 일부 변수만을 고려한 확률 분포

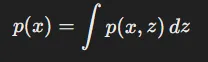
위의 수식은 x와 z로 이루어진 다변수 확률 분포 p를 x로만 나타내는 방법입니다. z를 소거해야하기 때문에 변수 z에 대해서 적분하는 과정을 거치면 x에대한 수식만을 구할 수 있습니다.

Expected Value(기댓값)

정의: 확률 변수 X가 가질 수 있는 모든 가능한 값들에 대해, 각 값에 해당하는 확률을 가중치로 곱하여 더한 값

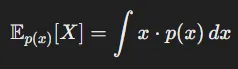
이산형 확률 변수: 모든 가능한 값에 대해 각 값에 해당하는 확률을 곱한 뒤 이를 합산한 값

연속형 확률 변수: 확률 밀도 함수 p(x)에 대해 적분을 수행

Bayes’ Rule

정의: 기존의 확률을 새로운 증거에 따라 업데이트하는 과정(사전확률 → 사후확률)

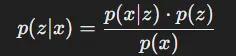
수식 정리: 기존의 확률(z)에 새로운 증거(x)가 들어온 상황

• $p(z|x)$: Posterior(사후 확률) → x가 주어졌을 때 z가 발생할 확률
• $p(x|z)$: Likelihood → z라는 조건 하에서 데이터 x가 관찰될 확률
• p(z): Prior(사전 확률) → z가 발생할 사전 정보에 근거한 확률
• p(x): Marginal Probability(주변 확률) → 관측된 데이터 x의 확률

[추가설명]

함수 p는 확률 밀도 함수(pdf)를 의미합니다.

예제: https://www.youtube.com/watch?v=Y4ecU7NkiEI

Kullback-Leibler(KL) Divergence

정의: 두 확률 분포 간의 차이를 측정하는 방법(동일하면 0)

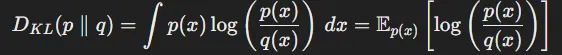
수식 정리: 확률 분포 p와 참조 분포 q 간의 KL 발산

• $p(x)$: 실제 확률 분포
• $q(x)$: 참조 확률 분포
• $\int p(x) \log \left( \frac{p(x)}{q(x)} \right) \, dx$: 두 확률 밀도 함수에 대해 적분을 수행해서 KL 발산을 계산

Jensen’s Inequality

정의: 볼록 함수(convex function)에서 두 점을 잇는 직선의 높이는 함수 곡선의 높이보다 크거나 같다.

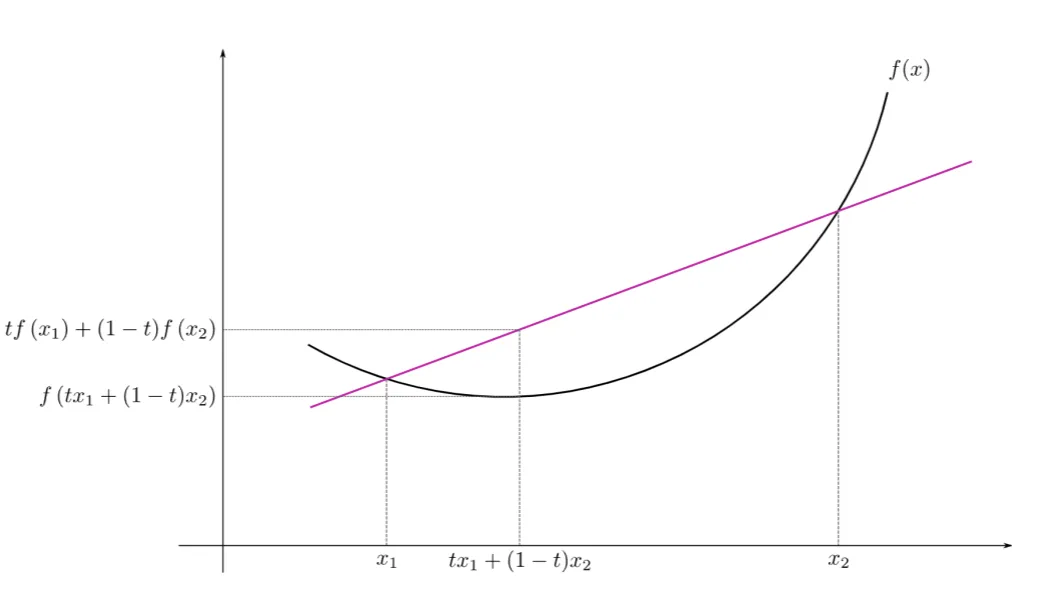
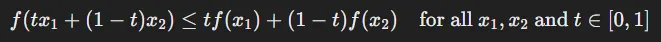
$tx_1 + (1-t)x_2$는 x2로부터 t의 비율만큼, x1으로부터 (1-t)비율만큼 떨어진 하나의 점입니다. 이때 이 두 점사이의 임의의 점에 대해서 볼록 함수의 함숫값은 두 직선보다 항상 아래에 있다는 것을 수식으로 나타낸 것입니다.

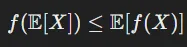
이를 기댓값에 적용한다면 기댓값을 먼저 취하고 함수에 적용한 값이, 함수에 먼저 적용하고 기댓값을 구한 값보다 작거나 같다는 것을 의미합니다.

이러한 정보는 엔트로피와 관련하여 기대 정보량을 계산하는데 사용됩니다.

Variational Autoencoder (VAE)

VAE는 주어진 실제 이미지 x에 대해, 그 이미지를 설명하는 latent variable(z)를 사용하여 marginal probability p(x)를 최대화하고자 합니다.

marginal probability인 p(x)는 이미지 x가 생성될 확률을 나타내며, 이는 VAE가 데이터 분포를 잘 설명하도록 만드는 중요한 목표. 조금더 쉽게 말하면, p(x)는 모델이 특정한 이미지와 같은 데이터를 얼마나 잘 설명하고 있는지를 나타냅니다.

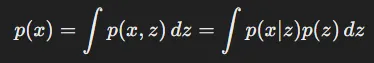
p(x)를 구하기 위해서는 위의 수식에서처럼 적분을 해야하는데 Monte-Carlo 방식은 시간이 매우 오래걸리기 때문에 적절하지 않습니다.

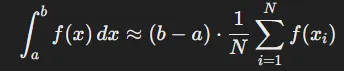
Monte-Carlo 방식은 적분 영역에서 무작위로 샘플($a$에서 $b$까지 적분한다 했을 때 그 사이의 $t$)에서의 값을 통해 근사하는 방법입니다. 수식은 위와 같습니다.

이 방식은 샘플링하는 개수가 많아질수록 성능이 좋아지고, 고차원에서 더 많은 영역을 커버할 수 있기 때문에 많은 샘플링 개수를 요구합니다. 하지만 많은 샘플링은 자연스럽게 많은 시간을 요구하기때문에 적절하지 않은 방법이라고 언급한 것입니다.

그렇다면 p(x)를 적분없이 구할 수 있는 방법은 존재할까요? 네 위에서 개념으로 배웠던것중에 정답이 있습니다. 바로 베이즈 정리입니다.

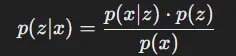
위의 수식에서 분모의 p(x)와 p(z|x)를 바꾼다면 우리가 원하는 p(x)를 구할 수 있습니다. 하지만 우리는 p(z|x)를 모르기 때문에 해당 값을 구해야 p(x)를 구할 수 있습니다.

• p(z): 정규분포로부터 구할 수 있습니다.
• p(x|z): Decoder를 통해서 구할 수 있습니다.

Evidence Lower Bound(ELBO)

정의: p(x)를 직접적으로 구할 수 없는 상황에서 lower bound를 최대화하는 방식으로 접근

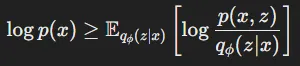
$q_\phi(z|x)$: 데이터 x가 주어졌을 때 latent variable z가 특정 값을 가질 확률 분포. 이는 Encoder에 의해 학습됩니다.

• 베이즈 정리에서 우리가 못구했던 p(z|x)를 근사하기 위해서 사용됩니다.
• 해당 값이 작아지면 데이터 x로부터 다양한 latent variable을 잘 설명할 수 있게됩니다.
• 반대로 해당 값이 커지면 데이터 x로부터 특정한 latent variable에 의존하게 됩니다.

$p(x,z) = p(x|z)p(z)$: latent variable z가 주어졌을 때 데이터 x를 얼마나 잘 표현하는가

즉, log안의 값이 커질수록 다양한 이미지의 데이터가 잘 생성된다는 것을 의미합니다.

이제 오른쪽 수식에 대해서는 이해가 갔는데 왜 갑자기 오른쪽 수식이 p(x)에 대한 lower bound냐라는 의문이 생길 것입니다. 이역시 위에서 배웠던 개념들을 가져오면 충분히 해결할 수 있습니다.

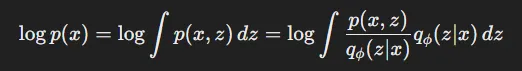
우선 p(x)를 marginal distribution을 이용해서 위의 수식처럼 바꿀 수 있습니다.

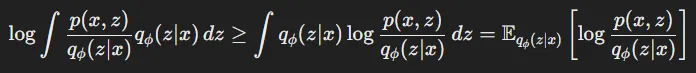
그다음 크거나 같다!의 개념은 Jensen’s inequality를 적용해서 위의 수식으로 나타낼 수 있습니다.

log라는 함수는 위의 개념에서 설명한 볼록함수가아닌 오목함수(위로 볼록)이기 때문에 수식이 반대로 적용됩니다. log를 f라는 함수로 치환하면 함수를 마지막에 적용한 왼쪾 수식이 오른쪽 수식보다 크거나 같다는 것을 알 수 있습니다.

또한 오른쪽 수식의 적분은 기댓값으로 정의할 수 있고 이를 나타낸 값이 바로 ELBO입니다.

ELBO수식을 분해하면 최종적으로 아래의 식이 나옵니다. 이때 첫번째 term은 Decoder가 잘 생성할 수록 값이 커지고, 두번째 term은 Encoder가 생성한 데이터의 분포가 z의 분포와 비슷해질수록 작아집니다.

즉 p(x)값을 최대화하기 위해서는 첫번째 term에서 Decoder가 학습을 잘하고, 두번째 term에서 Encoder가 학습을 잘해야되는 것입니다.

VAE Code

자료 출처: https://github.com/Jackson-Kang/Pytorch-VAE-tutorial/blob/master/01_Variational_AutoEncoder.ipynb

Encoder

latent variable z를 생성하는 과정. 이때 z는 평균과 분산 두가지 값을 갖습니다.

"""
    A simple implementation of Gaussian MLP Encoder and Decoder
"""

class Encoder(nn.Module):
    
    def __init__(self, input_dim, hidden_dim, latent_dim):
        super(Encoder, self).__init__()

        self.FC_input = nn.Linear(input_dim, hidden_dim)
        self.FC_input2 = nn.Linear(hidden_dim, hidden_dim)
        self.FC_mean  = nn.Linear(hidden_dim, latent_dim) # 평균을 위한 마지막 Layer
        self.FC_var   = nn.Linear (hidden_dim, latent_dim) # 분산을 위한 마지막 Layer
        
        self.LeakyReLU = nn.LeakyReLU(0.2)
        
        self.training = True
        
    def forward(self, x):
        h_       = self.LeakyReLU(self.FC_input(x))
        h_       = self.LeakyReLU(self.FC_input2(h_))
        mean     = self.FC_mean(h_)
        log_var  = self.FC_var(h_)                     # Encoder는 평균과 분산 2가지 값을 생성합니다. 
                                                       #             (i.e., parateters of simple tractable normal distribution "q"
        
        return mean, log_var

Decoder

평균과 분산을 갖는 latent variable z로부터 이미지 데이터 x를 생성하는 과정

주의: 입력값이 평균과 분산이 아닌 이 다음에서 다룰 z하나만 사용

class Decoder(nn.Module):
    def __init__(self, latent_dim, hidden_dim, output_dim):
        super(Decoder, self).__init__()
        self.FC_hidden = nn.Linear(latent_dim, hidden_dim)
        self.FC_hidden2 = nn.Linear(hidden_dim, hidden_dim)
        self.FC_output = nn.Linear(hidden_dim, output_dim) # Decoder는 이미지 데이터의 분포 p(x)만을 출력한다.
        
        self.LeakyReLU = nn.LeakyReLU(0.2)
        
    def forward(self, x):
        h     = self.LeakyReLU(self.FC_hidden(x))
        h     = self.LeakyReLU(self.FC_hidden2(h))
        
        x_hat = torch.sigmoid(self.FC_output(h)) # 생성된 이미지의 각 픽셀들에 대해서 0과 1사이의 픽셀 값을 갖도록 설정
        return x_hat
        

Model

Variational Autoencoder 설계

코드를 보기전에 reparameterization(재매개변수화)에 대해서 간단히 설명하도록 하겠습니다.

코드에서 보는 것처럼 reparmeterization의 역활은 랜덤한 노이즈를 분산에 추가하는 과정입니다.

해당 과정은 Encoder가 생성한 평균과 분산으로부터 랜덤한 샘플을 하나 뽑아야하는데, 이때 뽑는 과정에서 back propogation을 진행할 수 없다는 문제가 있었습니다. 이를 해결하기 위해 랜덤한 노이즈 epsilon을 추가해서 샘플링 과정을 미분가능하게 설정한 것입니다.

추가적으로 그냥 z = mean + var로 하면 안돼? 라는 의문이 들 수 있지만, 이는 확률분포에서 샘플링하는것이 아니라 그냥 하나의 값이 되기때문에 다양성이 떨어진다는 문제가 있습니다.

class Model(nn.Module):
    def __init__(self, Encoder, Decoder):
        super(Model, self).__init__()
        self.Encoder = Encoder
        self.Decoder = Decoder
        
    def reparameterization(self, mean, var):
        epsilon = torch.randn_like(var).to(DEVICE)        # 표준 정규분포에서 분산과 같은 형태를 샘플링    
        z = mean + var*epsilon                          # reparameterization trick
        return z
        
                
    def forward(self, x):
        mean, log_var = self.Encoder(x)
        z = self.reparameterization(mean, torch.exp(0.5 * log_var)) # log 분산을 그냥 분산으로 바꾸기 위해서 지수 값을 취해줍니다. + 분산을 표준편차로 바꿔주기 위해서 0.5를 곱합니다.
        x_hat            = self.Decoder(z)
        
        return x_hat, mean, log_var

loss

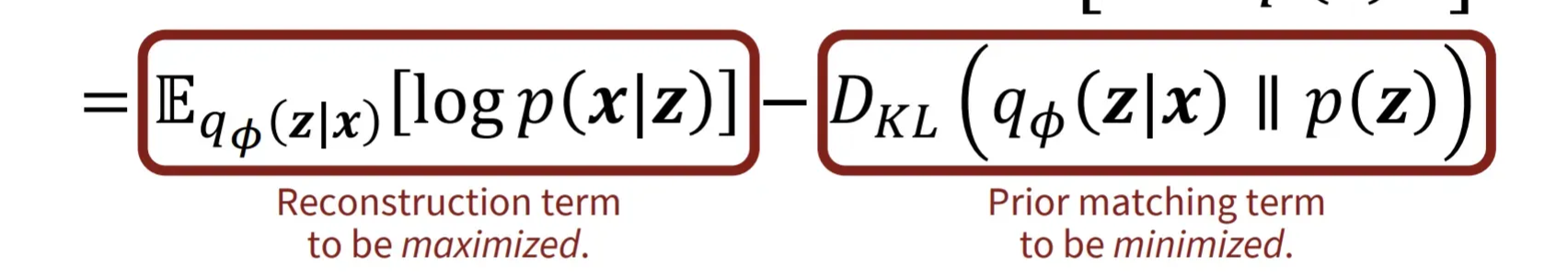
위의 수식을 코드로 구현한 파트입니다.

from torch.optim import Adam

BCE_loss = nn.BCELoss()

def loss_function(x, x_hat, mean, log_var):
    reproduction_loss = nn.functional.binary_cross_entropy(x_hat, x, reduction='sum') # 픽셀 단위로 차이를 계산
    KLD      = - 0.5 * torch.sum(1+ log_var - mean.pow(2) - log_var.exp()) # p(z|x)가 표준 정규분포 p(z)와 얼마나 다른지를 측정

    return reproduction_loss + KLD

optimizer = Adam(model.parameters(), lr=lr)

Train 코드 구현

print("Start training VAE...")
model.train()

for epoch in range(epochs):
    overall_loss = 0
    for batch_idx, (x, _) in enumerate(train_loader):
        x = x.view(batch_size, x_dim)
        x = x.to(DEVICE)

        optimizer.zero_grad()

        x_hat, mean, log_var = model(x)
        loss = loss_function(x, x_hat, mean, log_var)
        
        overall_loss += loss.item()
        
        loss.backward()
        optimizer.step()
        
    print("\tEpoch", epoch + 1, "complete!", "\tAverage Loss: ", overall_loss / (batch_idx*batch_size))
    
print("Finish!!")

구현 결과

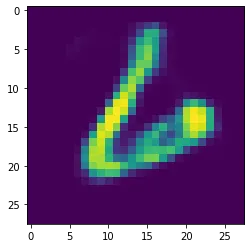
1. Reconstruction

입력값으로 들어간 이미지

VAE를 통해서 출력한 이미지

1. Noise → Image