출처[LECTURE03, LECTURE04]
강의 영상
https://www.youtube.com/watch?v=9V-7BoxEcqk
https://www.youtube.com/watch?v=--p26ltTUaU
해당 강의를 기반으로 추가적인 코드 구현과 설명을 정리했습니다.
Denoising Diffusion Probabilistic Models(DDPM)
VAE와의 비교
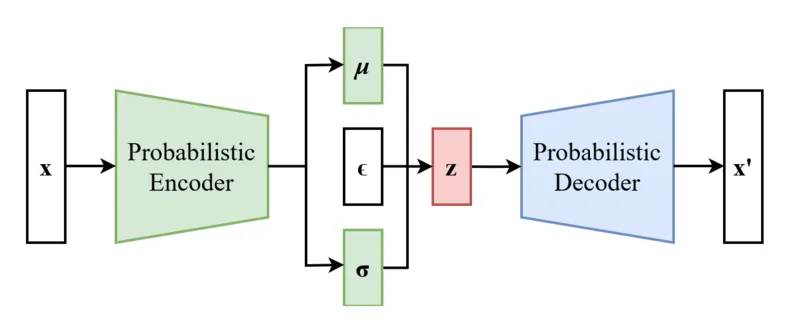
이전 강의에서 설명한 VAE의 모델 구조입니다. 간단하게 요약하면 Encoder를 통해서 latent variable을 학습하고, Decoder를 통해서 이를 이미지로 reconstruction 하는 과정을 진행합니다.
VAE의 단점은 어떤게 있을까요? latent varible은 기존 이미지보다 더 작은 벡터 값이기때문에 많은 정보를 포함하지 못합니다. 이러한 값으로 이미지를 생성하면 자연스럽게 부적절한 결과(blur한 결과)가 생성이 됩니다.
이를 극복하려면 어떻게 해야할까요? 차원이 줄어서 정보를 많이 포함하지 못한다면 차원을 줄이지 않으면 되는 것이고, 부적절한 z값이 생성된다면 z값을 잘 생성하도록 하면되는 것입니다.
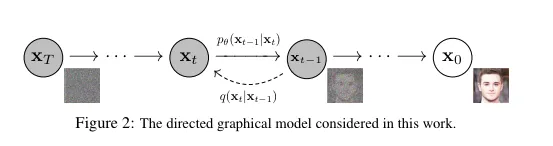
위의 그림은 DDPM의 모델 구조입니다. 기존에는 로부터 Encoder를 통해서 latent varibale을 구한다면, DDPM 에서는 노아즈를 여러단계로 더해가면서 동일한 차원의 latent variable인 를 생성하게됩니다. 그러면 이전에 말했던 단점인 부적절한 latent variable로 인해 생기는 문제를 해결할 수 있을 것입니다. 더자세한 내용을 아래에 이어서 설명하도록 하겠습니다.
Forward Process
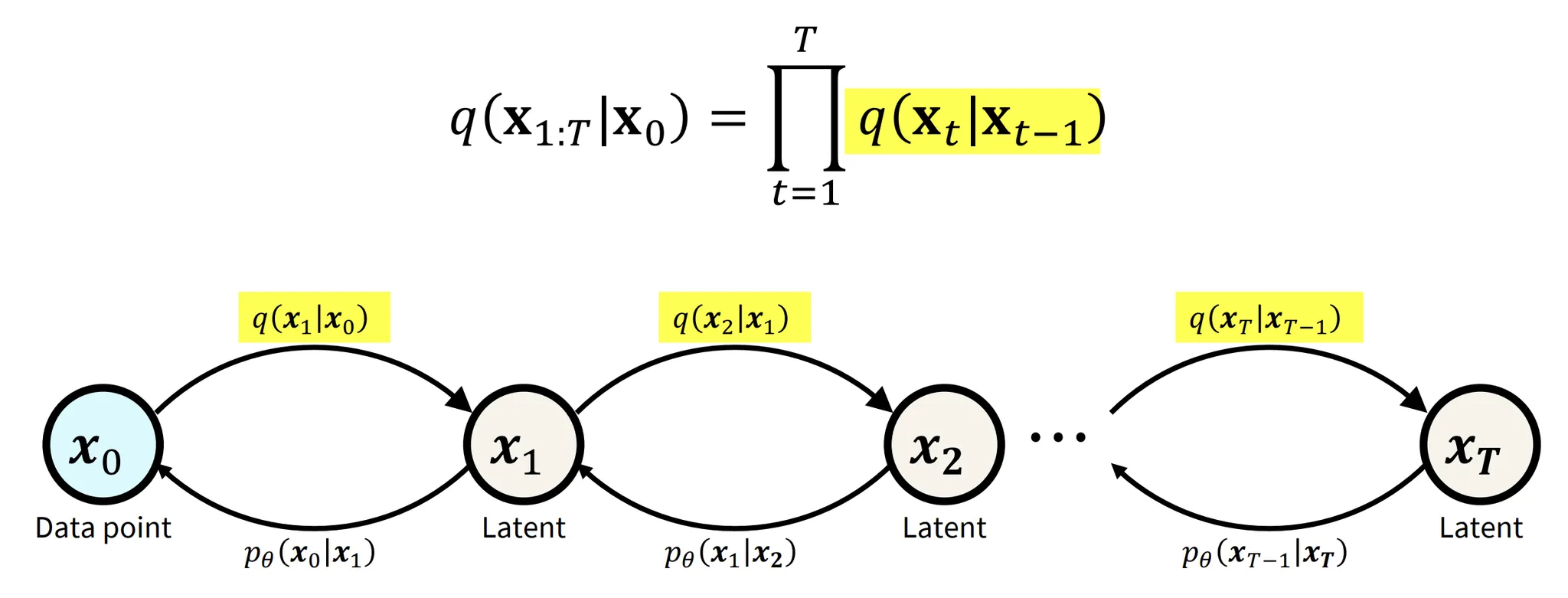
형광팬 쳐져있는 수식(부분)이 DDPM의 Foward Process입니다. VAE의 Encoder역할을 하는 부분이라고 생각하시면됩니다. 하지만 VAE와 다르게 고정된 노이즈가 들어가기때문에 학습하는 부분이 아닙니다. 따라서 수식을 적을 때도 세타값 없이 그냥 p만 적은 것을 확인할 수 있습니다.
요약하자면 노이즈를 점점 추가해서 데이터 분포를 가우시안 분포로 보내는 것입니다.
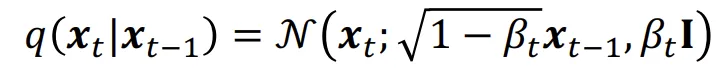
노이즈를 추가하는 과정을 수식으로 나타내면 위와 같습니다. 이전 step의 평균에 를 곱해주고, 분산에 를 곱해주는 과정으로 진행합니다. 위와 같이 노이즈를 더하는 과정을 Variance Preserving 방식에 해당합니다. 추후에 Variance Exploding 방식도 사용되니 궁금하신 분들은 찾아보시면 좋을거같습니다.
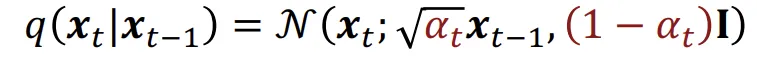
어쨌든 돌아와서 수식의 편의상 를 로 변경하면 수식은 위와같이 변경됩니다.
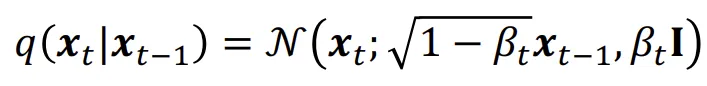
Forward Convergence
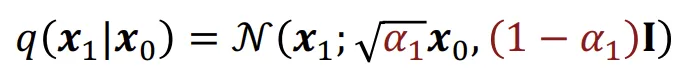
위의 수식을 바탕으로 를 구하라고하면 아마 쉽게 위와같이 나타낼 수 있을것입니다. 그렇다면 2단계 차이나는 는 어떻게 나타낼까요?
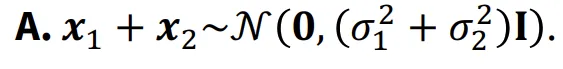
이에 대해서 설명하기 전에 기본적인 지식을 하나 설명해드리겠습니다. 2개의 분포의 합을 나타낼 때 평균은 그냥 더하고, 분산은 제곱해서 더하고 다시 루트를 씌웁니다(루트안의 합으로 나타내도 됩니다.)

다시 돌아와서 그러면 은 어떻게 구할까요? 위의 유도식처럼 를 으로 나타내고, 을 다시 으로(파란색 박스) 나타내주면됩니다. 이때 빨간색 박스의 유도과정은 2개의 노이즈에 대해서 선형 결합을 통해서 새로운 노이즈를 만들고, 여기에 두 분포의 분산을 합치는 것처럼 더하는 과정입니다.
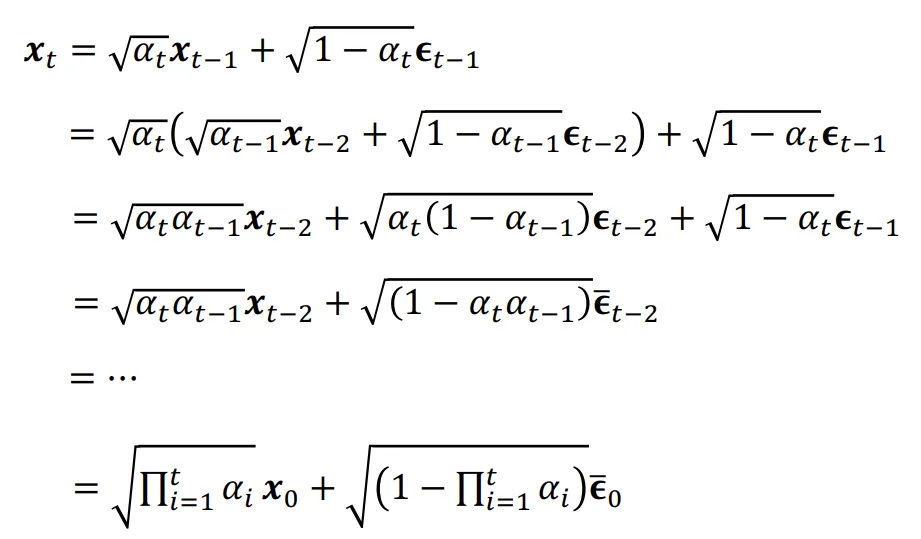
기왕 이렇게된거 쭉 다해서 까지 구해보도록 하겠습니다. 위와같이 유도한 결과입니다.
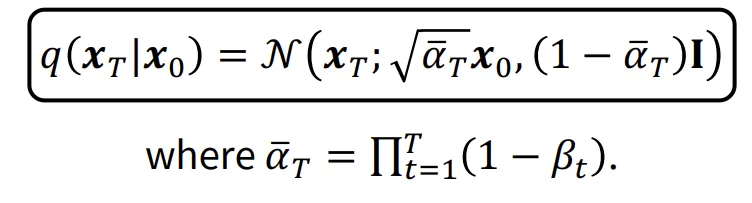
최종적인 수식은 위와같습니다. 여기서 저희는 시점의 분포가 가우시안 분포라는 것을 알고있습니다. 따라서 는 0이라는 것을 알 수 있습니다.
개인적으로 궁금했던 부분은 ‘데이터를 노이즈에 추가했는데 왜 가우시안 분포가 되는거지?’였습니다. 이거에 대한 구글링을 통해 얻은 답은 아래와 같습니다.
- 중심극한정리: 여러 독립적인 랜덤 변수의 합이 가우시안 분포로 수렴
- Markov Chain: 각 단계에서 직전(이전) 상태에만 의존합니다.
- Markov Chain 과정이 반복되면서 점점 더 무작위성이 데이터에 더해지고, 데이터의 모든 구조적 정보가 사라진 완전한 가우시안 노이즈로 변합니다.
Reverse process
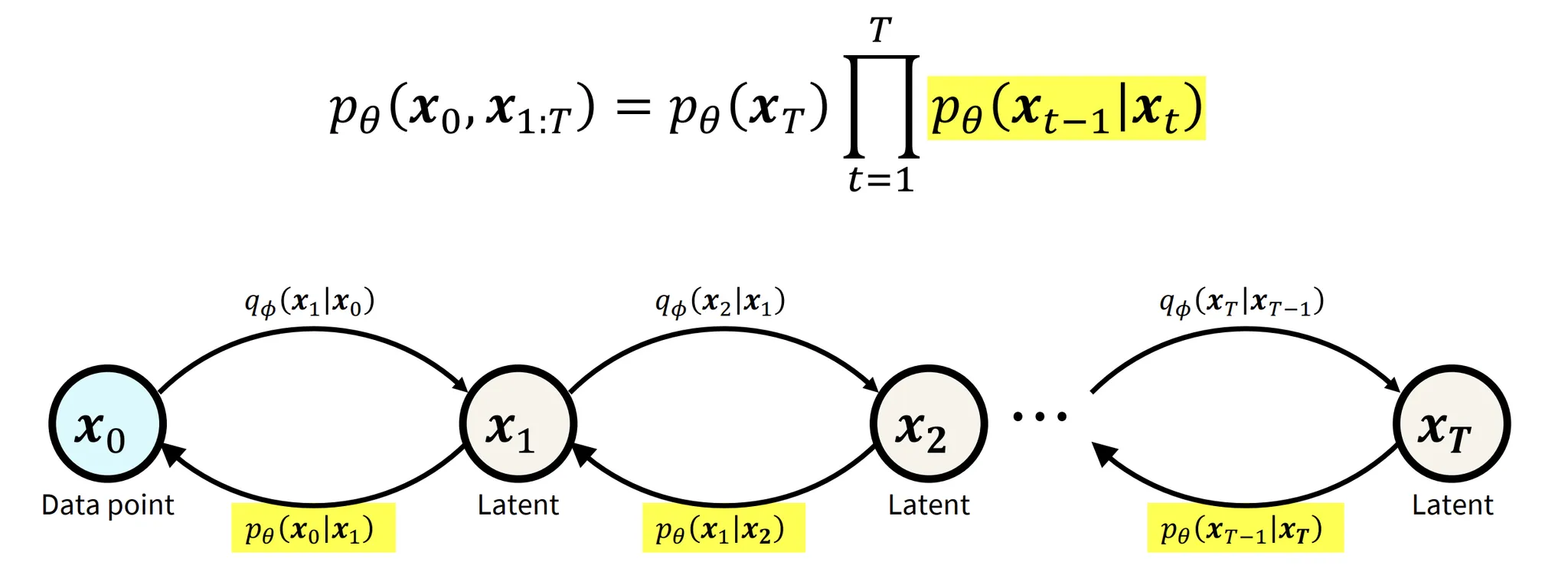
해당 사진의 형광팬 쳐져있는 부분이 Reverse process라고 보시면됩니다. Forward process를 통해서 가우시안 분포를 얻었다면, 이제 VAE의 Decoder부분처럼 이를 다시 이미지로 reconsturcion하는 부분이 reverse process입니다. Forward process에서 한 step마다 노이즈를 추가한 것처럼, reverse process에서는 한 step마다 제거할(추가된) 노이즈를 예측합니다.
ELBO
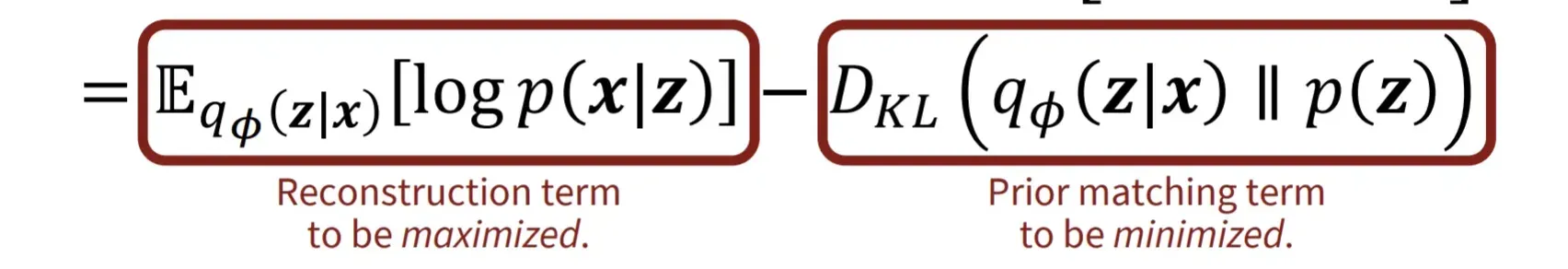
ELBO 역시 VAE와 비교해보겠습니다. ELBO는 p(x)를 직접적으로 정의할 수 없는 상황에서 lower bound를 최대화하는 방식입니다. ELBO 수식을 전개했을 때 위의 수식이 나옵니다. 위의 수식 중 첫번째 부분은 latent variable로부터 얼마나 데이터를 잘 생성하는지, 즉 Reconsturction term입니다. 두번째 부분은 주어진 데이터로부터 latent variable을 얼마나 잘 생성하는지, 즉 Encdoer의 성능과 관련된 term입니다.

이제 DDPM의 ELBO수식을 확인해보겠습니다. VAE와 비슷한 부분은 파란색 박스 부분으로 Reconstruction & Prior matching term 입니다. 3가지 수식을 하나하나 자세히 살표보도록 하겠습니다.
Prior matching term
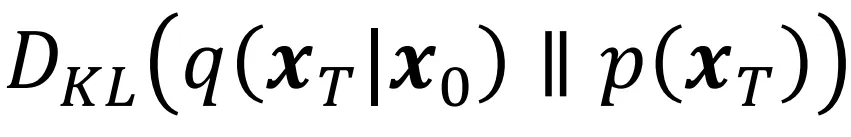
우리는 T시점의 분포를 가우시안 분포라고 알고있습니다. 빠라서 우리는 와 의 분포를 모두 알고있습니다. 두 값이 모두 가우시안 분포이므로 해당 KL Divergence의 값은 0입니다.
Reconstrucion term
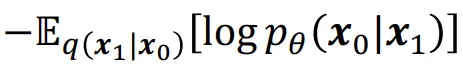
VAE와 동일하게 작동하지만, 마지막 step에서만 작동한다고 생각하면됩니다. 값이 맨아래 Denoising matching term에 비해 작기때문에 무시할만한 값이라고 설명하고 있습니다.
Denoising Matching Term
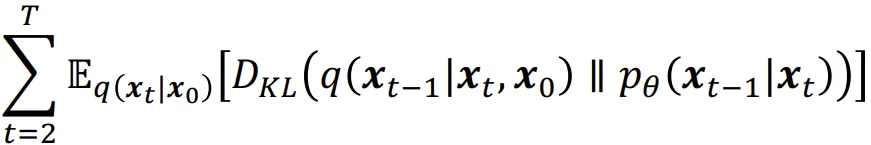
이전수식이 t-1~ T-1까지인데 여기에 t대신 t+1을 대입하면 위와같은 수식이 나옵니다.
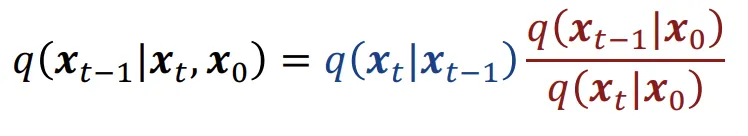
KL Divergence수식의 왼쪽 부분에 대해서 먼저 나타내면 베이즈 정리를 통해서 수식을 우항처럼 나타낼 수 있습니다.
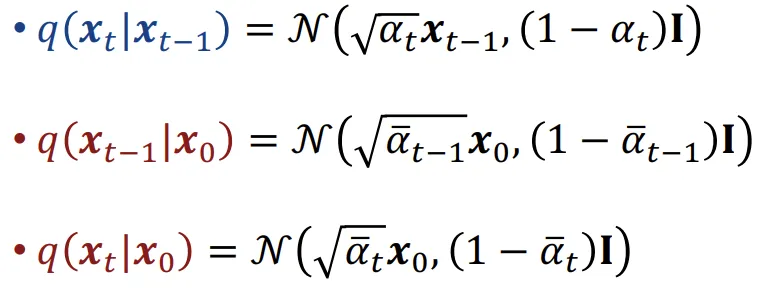
각각의 수식의 분포를 나타내면 위와같습니다.

이제 수식의 어려운 부분은 생략하고 결과를 나타내면 최종적으로 하나의 새로운 분포를 나타내게 됩니다. 지금 평균이 에 대해서 나타나있는데 모델이 노이즈를 기반으로 예측을 하도록 수정하기 위해서 에 대해서 다시 나타내도록 하겠습니다.
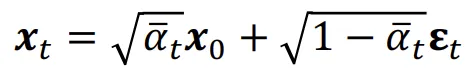
위의 수식은 을 통해서 를 에 대해서 나타낸 수식입니다. 이를 에 대해서 나타내면 아래와 같이 나타낼 수 있습니다.
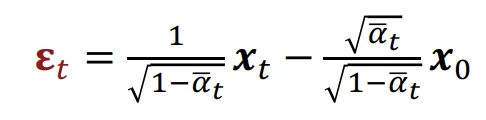
최종적으로 이를 이전의 평균에 대해서 대입하면 아래와 같은 수식이 나옵니다.
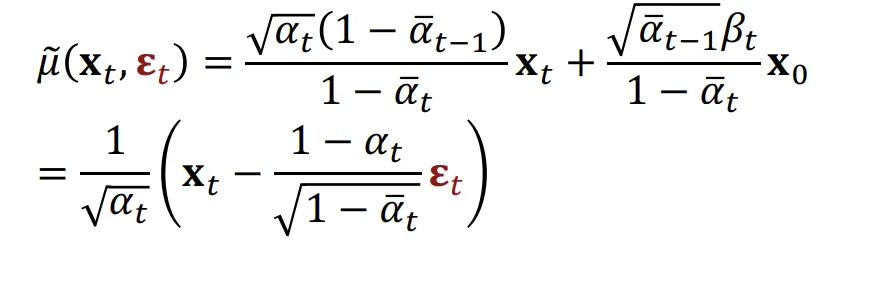
평균과, 노이즈, 와 의 수식을 위와같이 나타낼 수 있기때문에, 2가지 변수를 알고 있으면 나머지 하나의 변수를 알 수 있습니다.
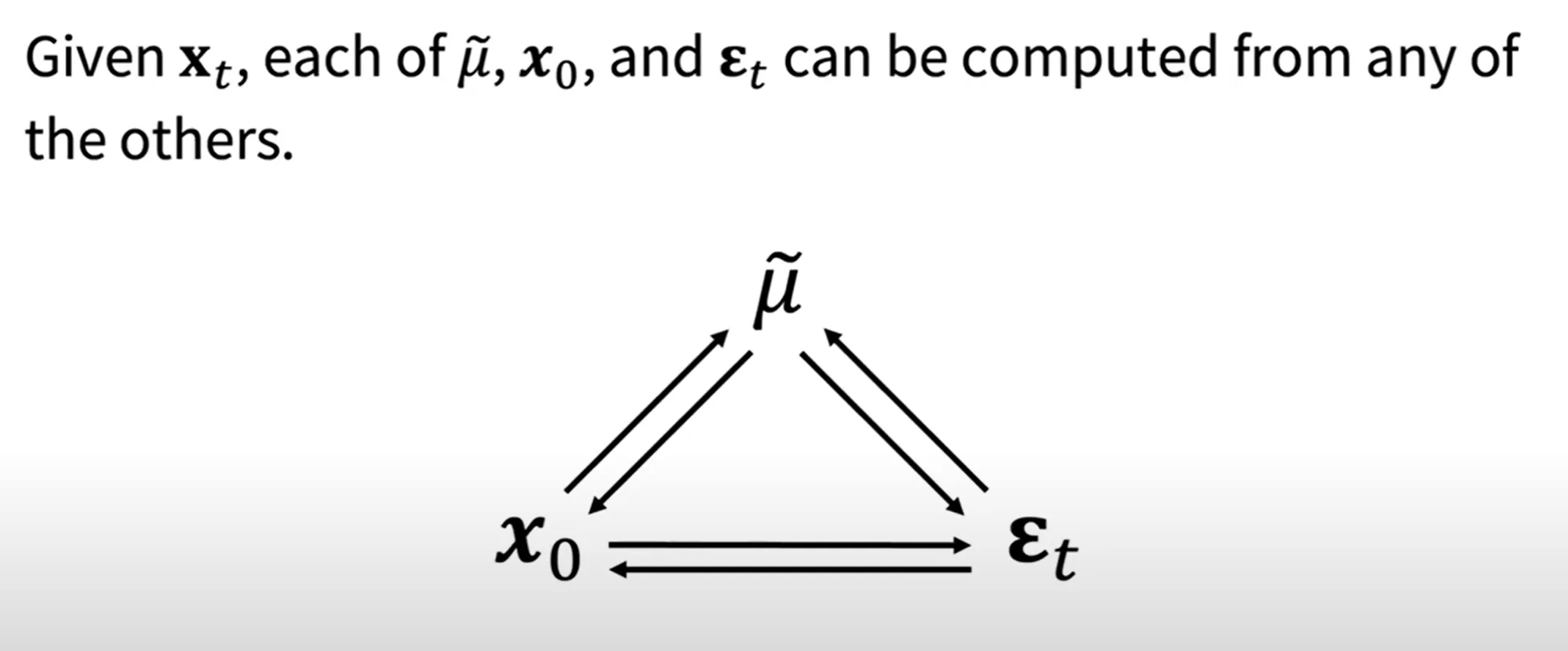
자 이제 다시 돌아와서 KL Divergence의 왼쪽 부분은 구했고, 오른쪽 부분 은 어떻게 구할까요?
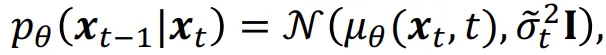
시간 t에서 제거할 노이즈를 예측하면 해당 값이 t-1시점의 데이터 분포가 될것이고 수식은 위와같습니다. 저희가 KL Divergence의 왼쪽 항을 길게 구해왔는데 최종값의 평균을 보면 와 에 대한 식인 것을 확인 할 수 있었습니다. 즉, 해당 값은 학습하는 값이 아닌 정해진(상수) 값입니다.
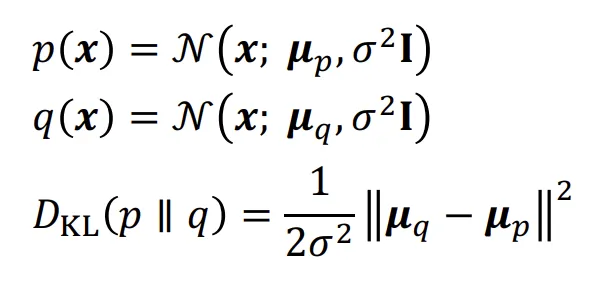
왼쪽식을 p(x), 오른쪽식을 q(x)라고 하면 수식은 위와같습니다. 분산이 동일하게 나타나있는데 이는 U-Net이 평균과 분산을 함께 예측하면 불안정해서 fix해서 평균만 예측하도록 진행했다고합니다.(추후 2개다 예측 하는 논문도 나오긴 했습니다.) 어쨌든 결론적으로 분산이 고정되었기 때문에 KL Divergence식은 위와같이 간소화될것입니다.
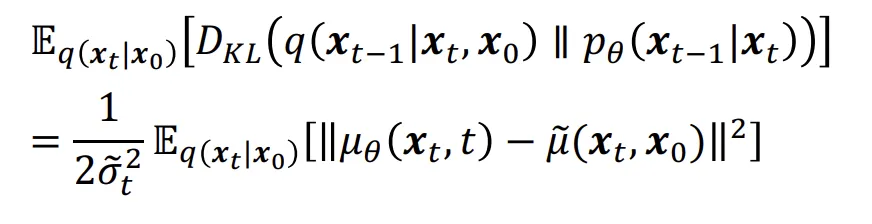
최종적으로 평균을 예측하는 네트워크의 식은 위와같은 loss를 최소화하면서 학습을 진행하게됩니다.
Predictor
지금까지 한 step에서 다음 step까지의 과정에서 평균을 예측하는 network를 학습하는 방법에 대해서 알아봤는데, 만약에 를 예측하는 network로 나타내면 어떻게 나타낼 수 있을까요?
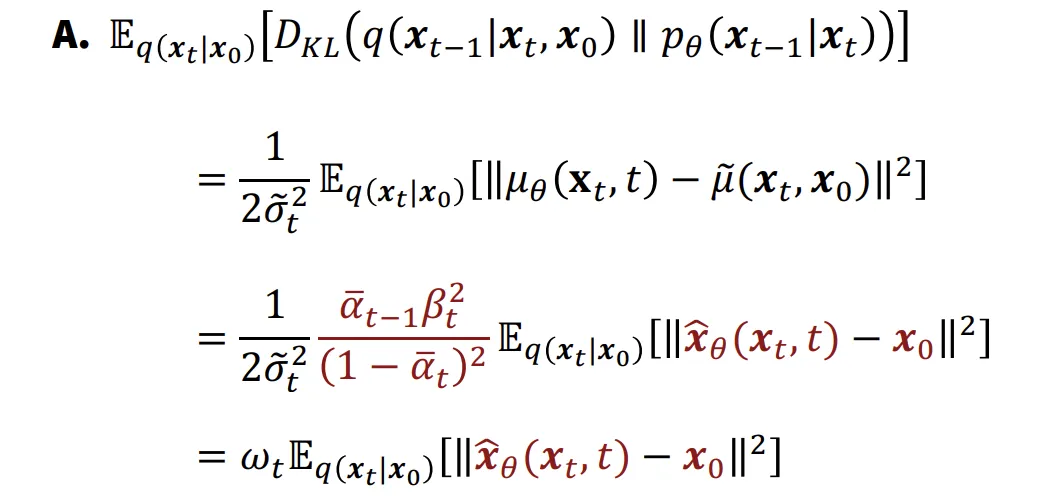
수식의 유도과정은 이해를 잘 못해 생략하도록 하겠습니다.(구글링 해도 이해불가..) 결론적으로 맨 아래와같은 형태의 식이 나오게됩니다. 위의 network를 학습하게 되면 시점에서 시점으로의 복원이 가능해지게 됩니다.
Predictor
이제 위의 predictor가아니라, 노이즈를 예측하는 Predictor로 설계하면 어떻게 될까요?
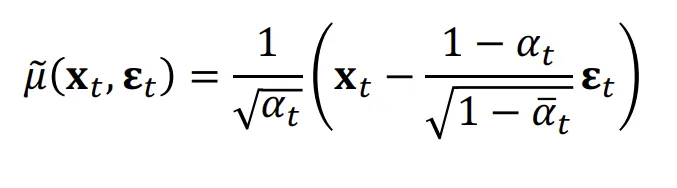
이전에 노이즈에대해서 평균을 나타낸 수식입니다. 이를 KL Divergence에 대입해서 최종적으로 나타맨 아래와 같은 형태입니다.
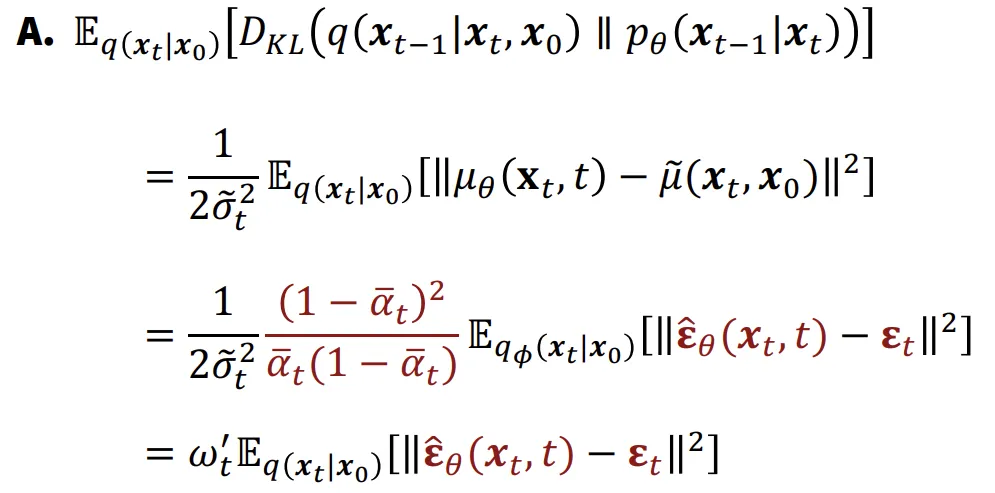
따라서 평균, , 를 예측하는 3가지 방식을 아래와 같이 나타낼 수 있습니다.
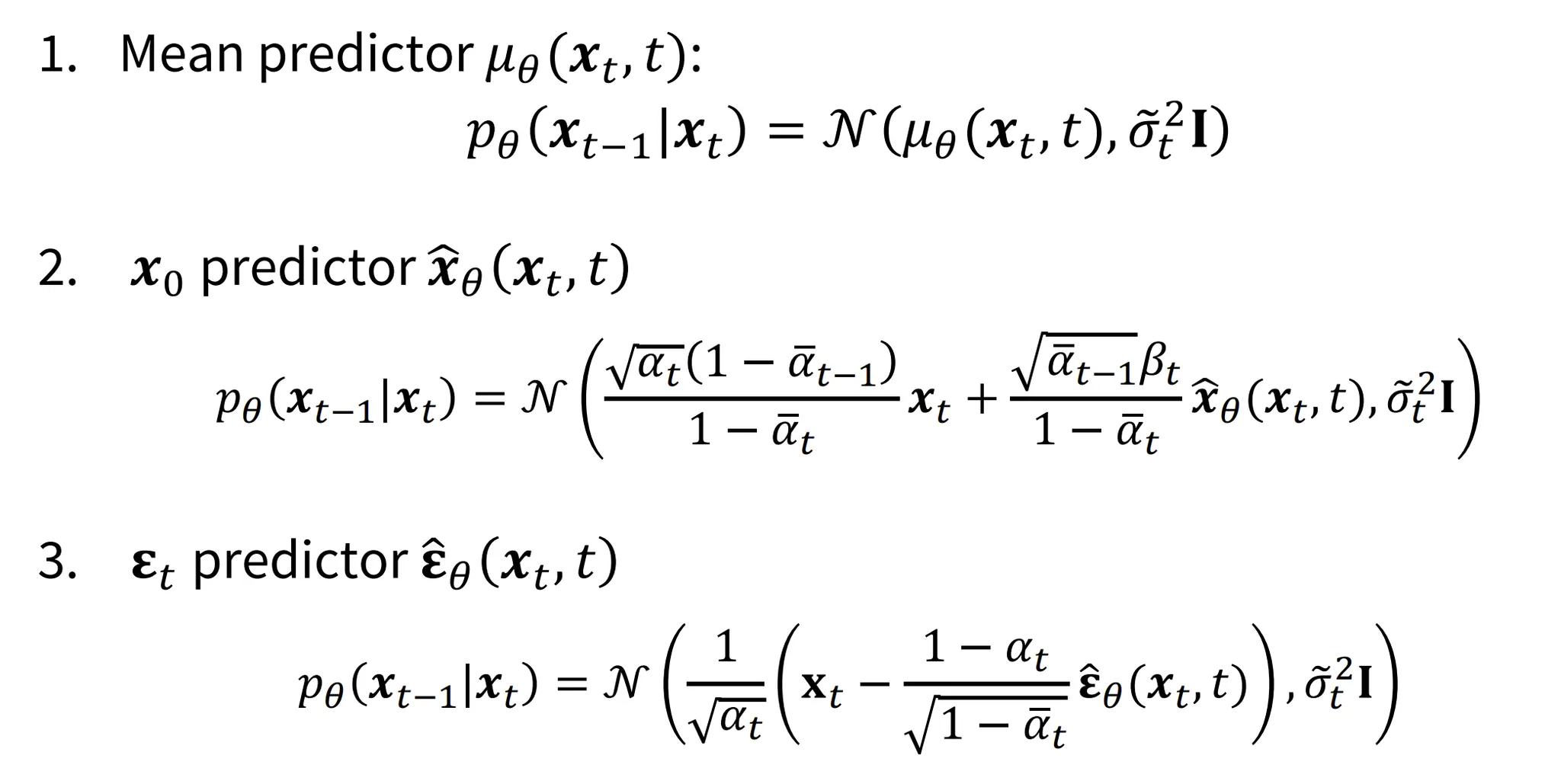
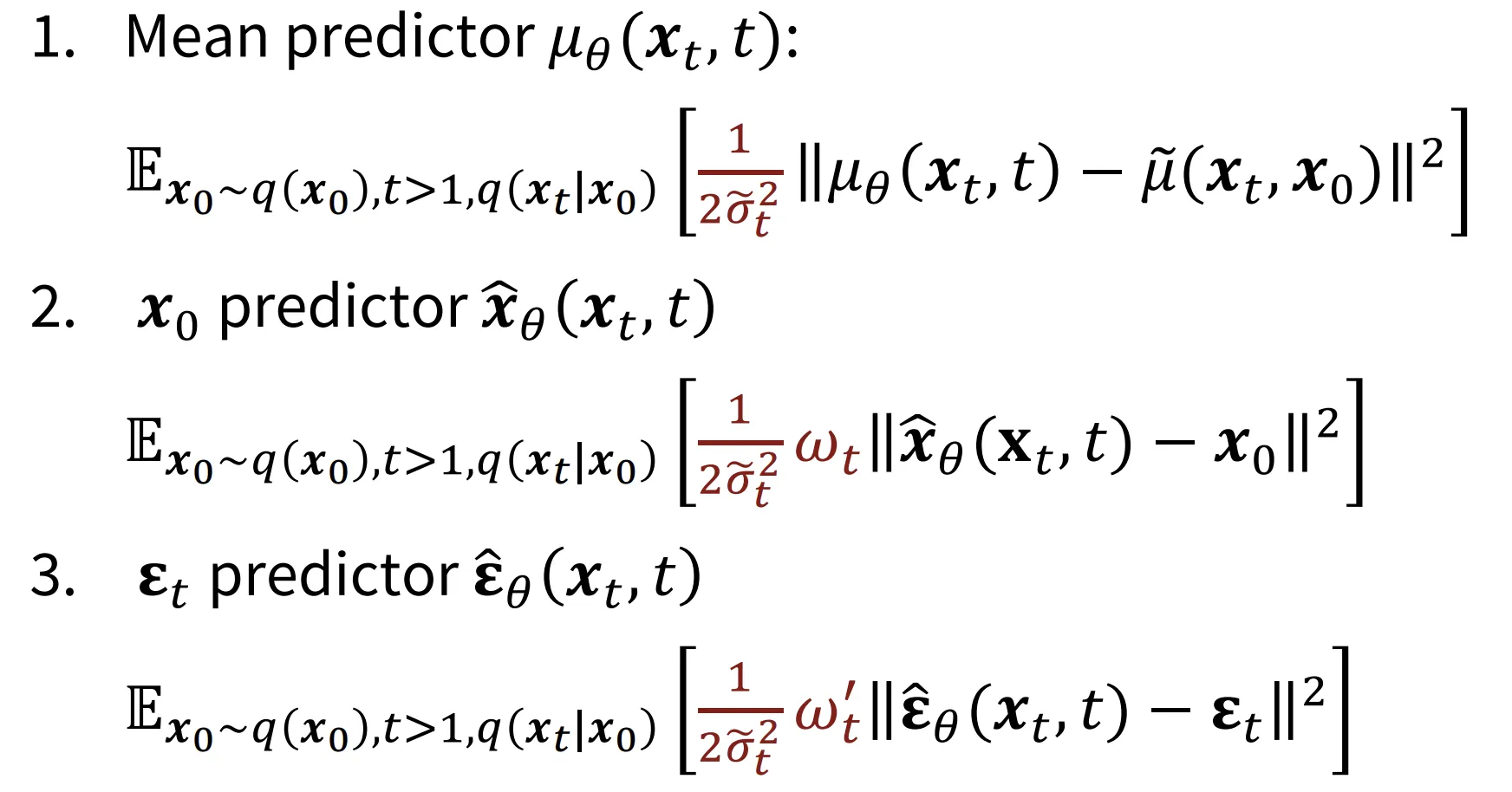
2번째 사진에서 나타난 weight term(빨간색 부분)은 실질적으로 학습의 편의성을 위해서 제거합니다.
사실상 3가지 predictor는 차이가 없고 일반적으로 predictor를 사용합니다. 왜냐하면 노이즈만을 예측하기때문에 수학적으로 간단하고 계산 효율성이 높기때문입니다.
분산이 고정되어있기 때문에 평균과 노이즈 예측은 거의 비슷하게 작동합니다. 평균은 에서의 분포가 a+b이고 에서의 분포가 a라면 a라는 분포를 예측하는 것이고, 노이즈 예측은 b만 예측하면 되는 것입니다. 일반적으로 노이즈가 일반 데이터 분포의 평균보다 계산하기 쉽기때문에 노이즈 예측을 일반적으로 사용하게 된 것입니다.
Training
- 랜덤한 이미지(데이터) 선택
- 랜덤한 시간 step(t) Sampling
- 노이즈 Sampling
- 2번에서 정한 시간에서의 노이즈 값을 가져오는 것입니다.
- 시간에 따라 노이즈가 미리 정해져있습니다. → 상수 & 코사인 스케줄러 등
- 계산
- 계산
- 노이즈 예측 모델을 통해서 시간 t에서의 노이즈를 예측하고 차이를 최소화
의문들 정리
- 위의 Training 과정에서 4번의 t시점의 데이터 분포는 왜 필요한가?
노이즈의 차이만 예측하는건데 왜 4번의 t시점의 데이터가 필요하는지 의문이 생길수도 있을 것입니다. 실제로 노이즈를 예측하기 위해서 U-Net 모델을 사용하는데 이 모델의 입력값으로 들어가는 데이터이기 때문에 4번의 데이터가 필요한 것입니다.
정리하자면 U-Net모델의 입력값으로 t시점의 데이터 분포(평균)과 t라는 step이 들어가면, 초기 시점(0)으로 돌아가기 위해 제거해야할 노이즈를 예측하는 것입니다.
- Inference과정은 어떻게 진행되는가?
훈련할 때 랜덤한 시점 t에서 0시점으로의 노이즈 예측을 하도록 설계되어있는데, inference할때는 왜 T에서 0로 한번에 안가고 모든 step을 다 가는지 궁금했었습니다.
이를 위해서 inference 과정을 이해하는게 중요합니다.
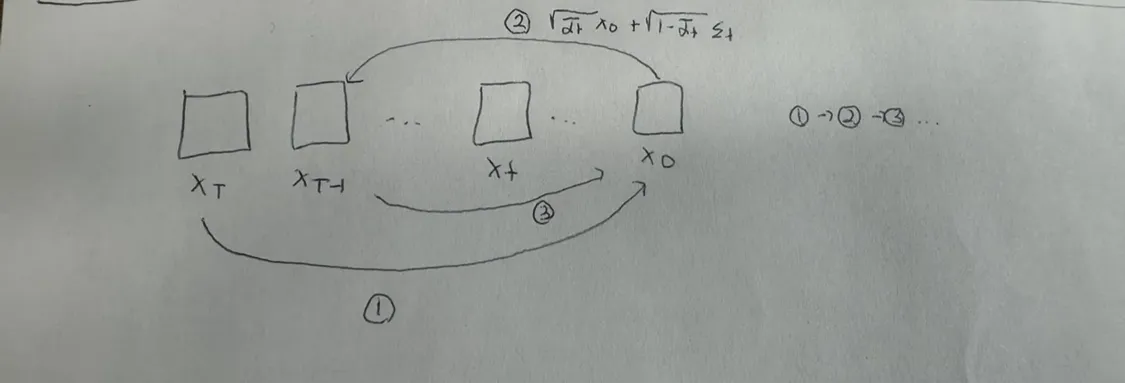
Inference과정을 그림으로 나타내면 위와같습니다. T시점에서 T-1시점으로 바로 넘어가는게 아니라 T시점에서 초기 시점(0)으로 노이즈를 예측해서 이동한후(1), 다시 T-1시점으로 이동(2), 다시 초기 시점으로 이동(3) 이렇게 반복되는 과정으로 진행됩니다.
- 왜 t → t-1로의 노이즈 예측이 아닌 t → 0으로의 노이즈 예측?
자연스럽게 위의 inference 과정을보면 T → T-1로 바로 못가고 0을 거쳐간다는 단점이 존재합니다. 그래서 왜 이렇게 진행되나 알아보니 만약 t → t-1로의 노이즈 예측을 하기 위해서 t시점의 노이즈와 t-1시점의 노이즈의 차이를 알아야하므로 2개의 노이즈 값을 알아야합니다. 반면에 이전처럼 무조건 초기 시점으로의 노이즈 예측을 한다면 1개의 노이즈 값만을 알아도됩니다. 즉 계산의 효율성을 위해서 노이즈의 값을 1개만 쓰는 초기시점으로의 노이즈 예측 방식으로 진행하도록 설계한 것입니다.
코드 정리
코드 출처: https://github.com/aju22/DDPM/blob/main/Denoising_Diffusion_Probabilistic_Model_(DDPMs).ipynb
linear_scheduler(선형 스케줄러)
노이즈를 더할 때 사용하는 선형 스케줄러. timesteps 개수만큼 나눠줍니다.
def linear_scheduler(timesteps, start=0.0001, end=0.02):
"""
Returns linear schedule for beta
"""
return torch.linspace(start, end, timesteps)get_index_from_list
Time step t에서의 value(노이즈) 값을 가져옵니다.
def get_index_from_list(vals, t, x_shape):
"""
Returns values from vals for corresponding timesteps
while considering the batch dimension.
"""
batch_size = t.shape[0]
output = vals.gather(-1, t.cpu())
return output.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)forward_diffusion_sample
초기(주어진) 이미지로부터 time step t의 노이즈를 더해서, 노이즈가 섞인 이미지 x_t 생성
def forward_diffusion_sample(x_0, t, device="cpu"):
"""
Takes an image and a timestep as input and
returns the noisy version of it after adding noise t times.
"""
noise = torch.randn_like(x_0) # x_0와 크기가같은 정규분포 노이즈 생성
# 노이즈 계수의 누적곱을 미리 입력하고(values), 이를 기반으로 t 시점의 노이즈를 가져옵니다.
sqrt_alphas_cumprod_t = get_index_from_list(sqrt_alphas_cumprod, t, x_0.shape) # sqrt_alphas_cumprod: 각 타임스텝에서의 노이즈 계수의 누적 곱
sqrt_one_minus_alphas_cumprod_t = get_index_from_list(sqrt_one_minus_alphas_cumprod, t, x_0.shape) # 1 - a값으로 논문의 B 값을 나타냅니다.
# mean + variance
return sqrt_alphas_cumprod_t.to(device) * x_0.to(device) + sqrt_one_minus_alphas_cumprod_t.to(device) * noise.to(device), noise.to(device)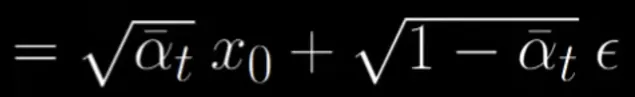
반환값: 위의 수식에 해당하는 값
- sqrt_alphas_cumprod과 sqrt_one_minus_alphas_cumprod는 전역변수로 값을 넘겨줌
Parameter
# Define beta schedule
T = 300 # time steps
betas = linear_scheduler(timesteps=T) # 논문에서 사용하는 노이즈 계수 값인 Beta
# Pre-calculate different terms for closed form
alphas = 1. - betas # 계산의 편의성을 위해 논문에서 정의한 1 - Beta 값인 Alpha
alphas_cumprod = torch.cumprod(alphas, axis=0) # alpha의 누적곱
# 이전 스텝값을 참조하기 용이하게 수정. 첫번째는 이전 값이 없기때문에 1.0
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0) # 마지막 값을 제외하고, 첫번째에 1.0을 추가
sqrt_recip_alphas = torch.sqrt(1.0 / alphas) # alpha의 역수 제곱근
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod) # 노이즈의 누적곱의 제곱근(논문에서 alpha위에 - 있는 부분)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)추가설명: alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
- t단계에서 Sampling을 할 때 t-1까지의 누적된 노이즈 값을 이용해서 계산을 합니다.
- 이전시점의 노이즈 * 현재 시점에서 예측한 노이즈 → 우리가 원하는 노이즈 값
- 여기서 말하는 첫번째 단계는 T → T-1로가는 단계입니다.
U-Net
ConvBlock
class ConvBlock(nn.Module):
def __init__(self, in_ch, out_ch, time_emb_dim, up=False):
super().__init__()
self.time_mlp = nn.Linear(time_emb_dim, out_ch) # conditon으로 들어간 time step을 동일한 차원으로 변환
if up: # 업샘플링
self.conv1 = nn.Conv2d(2*in_ch, out_ch, 3, padding=1)
self.transform = nn.ConvTranspose2d(out_ch, out_ch, 4, 2, 1) # Stride = 2
else:
self.conv1 = nn.Conv2d(in_ch, out_ch, 3, padding=1)
self.transform = nn.Conv2d(out_ch, out_ch, 4, 2, 1) # Stride = 2
self.conv2 = nn.Conv2d(out_ch, out_ch, 3, padding=1)
self.bn1 = nn.BatchNorm2d(out_ch)
self.bn2 = nn.BatchNorm2d(out_ch)
self.relu = nn.ReLU()
def forward(self, x, t, ):
h = self.bn1(self.relu(self.conv1(x))) # h: [batch_size, out_ch, height, width]
# Time embedding
time_emb = self.relu(self.time_mlp(t))
# Extend last 2 dimensions
time_emb = time_emb[(..., ) + (None, ) * 2] # [batch_size, out_ch] -> [batch_size, out_ch, 1, 1]
# Add time channel
h = h + time_emb # time_emb: [batch_size, out_ch, 1, 1] -> [batch_size, out_ch, height, width]
h = self.bn2(self.relu(self.conv2(h)))
# Down or Upsample
return self.transform(h)PositionalEncoding
시간 정보(time)를 받아서 위치 임베딩 벡터로 변환
class PositionalEncoding(nn.Module):
def __init__(self, dim):
super().__init__()
self.dim = dim
def forward(self, time):
device = time.device
half_dim = self.dim // 2 # 반은 cos, 반은 sin
embeds = math.log(10000) / (half_dim - 1)
embeds = torch.exp(torch.arange(half_dim, device=device) * -embeds) # 0부터 half_dim-1까지 정수를 생성하고, -embeds에 곱합니다.
embeds = time[:, None] * embeds[None, :] # embeds: (batch_size, half_dim)
embeds = torch.cat((embeds.sin(), embeds.cos()), dim=-1) # cos, sin을 하나로 합칩니다.
return embeds # embeds: (batch_size, dim)U-Net
class Unet(nn.Module):
"""
A simplified Unet architecture.
"""
def __init__(self):
super().__init__()
image_channels = 3
down_channels = (64, 128, 256, 512, 1024)
up_channels = (1024, 512, 256, 128, 64)
out_dim = 1
time_emb_dim = 32
# Time embedding
self.time_mlp = nn.Sequential(
PositionalEncoding(time_emb_dim),
nn.Linear(time_emb_dim, time_emb_dim),
nn.ReLU()
)
self.conv0 = nn.Conv2d(image_channels, down_channels[0], 3, padding=1)
# Downsample
self.downs = nn.ModuleList([ConvBlock(down_channels[i], down_channels[i+1],
time_emb_dim) for i in range(len(down_channels)-1)])
# Upsample
self.ups = nn.ModuleList([ConvBlock(up_channels[i], up_channels[i+1],
time_emb_dim, up=True) for i in range(len(up_channels)-1)])
self.output = nn.Conv2d(up_channels[-1], 3, out_dim)
def forward(self, x, timestep):
# Embedd time
t = self.time_mlp(timestep)
x = self.conv0(x)
# Unet
residual_inputs = []
for down in self.downs:
x = down(x, t)
residual_inputs.append(x)
for up in self.ups:
residual_x = residual_inputs.pop()
x = torch.cat((x, residual_x), dim=1)
x = up(x, t)
return self.output(x)Loss
get_loss(model, x_0, t)
def get_loss(model, x_0, t):
x_noisy, noise = forward_diffusion_sample(x_0, t, device) # t 시점의 이미지와 노이즈
noise_pred = model(x_noisy, t) # U-Net모델이 예측한 노이즈
return F.l1_loss(noise, noise_pred) # L1 Loss로 두 노이즈 차이 반환sample_timestep(x, t)
@torch.no_grad() # 학습을 안하도록 설정합니다.
def sample_timestep(x, t): # x: 노이즈가 추가된 이미지 // t: 현재 time step
"""
Calls the model to predict the noise in the image and returns
the denoised image.
"""
betas_t = get_index_from_list(betas, t, x.shape) # time step t에서의 노이즈 값을 가져옵니다.
sqrt_one_minus_alphas_cumprod_t = get_index_from_list(
sqrt_one_minus_alphas_cumprod, t, x.shape
) # t시점의 1-alpha 제곱근의 누적곱
sqrt_recip_alphas_t = get_index_from_list(sqrt_recip_alphas, t, x.shape) # t시점의 alpha 역수 제곱근
# Call model (current image - noise prediction)
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t # 노이즈를 비율에 맞게 제거
) # 노이즈 예측
posterior_variance_t = get_index_from_list(posterior_variance, t, x.shape)
if t == 0:
return model_mean
else:
noise = torch.randn_like(x)
return model_mean + torch.sqrt(posterior_variance_t) * noise
sample_plot_image(): 데이터 시각화
@torch.no_grad()
def sample_plot_image():
# Sample noise
img_size = IMG_SIZE
img = torch.randn((1, 3, img_size, img_size), device=device) # 초기 이미지를 가우시안 분포로 지정
plt.figure(figsize=(15,15))
plt.axis('off')
num_images = 10 # 전체 Step(300)을 10으로 나눈 것 -> 30 step씩 시각화
stepsize = int(T/num_images)
for i in range(0,T)[::-1]:
t = torch.full((1,), i, device=device, dtype=torch.long) # 현재 time step i에서 Tensor 생성
img = sample_timestep(img, t) # time step 노이즈를 제거한 이미지
if i % stepsize == 0: # 30의 배수인경우 시각화
plt.subplot(1, num_images, i/stepsize+1)
show_tensor_image(img.detach().cpu())
plt.show() Dataset
data = torchvision.datasets.StanfordCars(root=".", download=True)- 해당 코드를 그냥 실행하게 되면 오류가 발생하게 되고, https://github.com/pytorch/vision/issues/7545#issuecomment-1631441616 링크에서 나온 설명을 기반으로 데이터를 직접 다운로드해야합니다. (코랩 사용시 상당한 시간 소요)
show_images: 데이터 시각화
# 데이터셋에서 20개의 데이터를 시각화
def show_images(datset, num_samples=20, cols=4):
""" Plots some samples from the dataset """
plt.figure(figsize=(15,15))
for i, img in enumerate(data):
if i == num_samples:
break
plt.subplot(num_samples/cols + 1, cols, i + 1)
plt.imshow(img[0])load_transformed_dataset(): 데이터 전처리
def load_transformed_dataset():
'''
Returns data after applying appropriate transformations,
to work with diffusion models.
'''
data_transforms = [
transforms.Resize((IMG_SIZE, IMG_SIZE)), # 이미지 크기 변환
transforms.RandomHorizontalFlip(), # augmentation(이미지 좌우 변환)
transforms.ToTensor(), # Scales data into [0,1]
transforms.Lambda(lambda t: (t * 2) - 1) # Scale between [-1, 1] -> Normalization
]
data_transform = transforms.Compose(data_transforms) # 위의 여러가지 변환 작업을 순서대로 적용
train = torchvision.datasets.StanfordCars(root=".", download=True,
transform=data_transform)
test = torchvision.datasets.StanfordCars(root=".", download=True,
transform=data_transform, split='test')
return torch.utils.data.ConcatDataset([train, test])show_tensor_image(image): 이미지를 역변환해서 시각화
def show_tensor_image(image):
'''
Plots image after applying reverse transformations.
'''
reverse_transforms = transforms.Compose([
transforms.Lambda(lambda t: (t + 1) / 2), # [-1,1] -> [0,1]
transforms.Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
transforms.Lambda(lambda t: t * 255.), # [0,1] -> [0,255]
transforms.Lambda(lambda t: t.numpy().astype(np.uint8)),
transforms.ToPILImage(),
])
if len(image.shape) == 4: # batch가 포함되어있는 경우 첫번째 이미지를 사용
image = image[0, :, :, :]
plt.imshow(reverse_transforms(image))이미지에 노이즈를 점진적으로 추가하는 과정을 시각화
image = next(iter(dataloader))[0]
plt.figure(figsize=(15,15))
plt.axis('off')
num_images = 10
stepsize = int(T/num_images)
for idx in range(0, T, stepsize):
t = torch.Tensor([idx]).type(torch.int64)
plt.subplot(1, num_images+1, (idx/stepsize) + 1)
image, noise = forward_diffusion_sample(image, t)
show_tensor_image(image)Train
model.to(device)
optimizer = Adam(model.parameters(), lr=3e-4)
epochs = 100
for epoch in range(epochs):
for step, batch in enumerate(dataloader):
optimizer.zero_grad()
t = torch.randint(0, T, (BATCH_SIZE,), device=device).long()
loss = get_loss(model, batch[0], t)
loss.backward()
optimizer.step()
if epoch % 5 == 0 and step == 0:
print(f"Epoch {epoch} | step {step:03d} Loss: {loss.item()} ")
sample_plot_image()