코드및 간단한 설명: https://velog.io/@guts4/Basic-Generative-Model-DDPM
DDPM Background 수식 설명
Reverse process
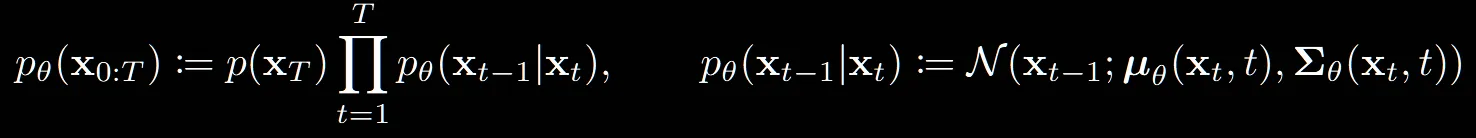
: reverse process를 나타내는 수식입니다.
: T시점에서의 데이터의 분포, 즉 가우시안 분포를 나타냅니다.
오른쪽 수식은 하나의 step이 진행되는 과정으로서 U-Net모델을 통해서 평균과 분산을 예측하는 과정입니다.
수식을 설명하자면, 초기시점 T에서 시작해서 하나의 step마다 평균과 분산을 예측하면서 최종적으로 데이터를 생성해내는 과정입니다. forward process와 달리 U-Net 모델을 학습해야하는 reverse process는 p아래에 가 붙은 것을 확인할 수 있습니다.
Forward process
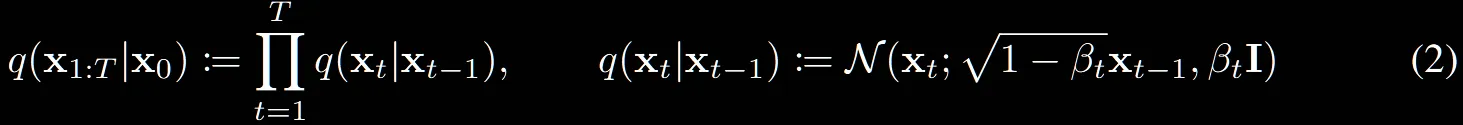
: forward process를 나타내는 수식입니다.
오른쪽 수식은 하나의 step이 진행되는 과정으로서 정해진 스케줄러에 따라서 만큼의 노이즈가 평균과 분산에 추가되는 과정입니다.
수식을 설명하자면, 위의 reverse process와 달리 정해진 상수로부터 노이즈를 입력 데이터에 추가하는 과정입니다. 즉 학습하는 과정이 없기때문에 가 없는 단순히 q로 정의된 과정입니다.
또한 맨왼쪽에 reverse process는 를 곱해주면서 T시점에서 시작한다고 나와있는데, Forward process는 조건부 분포이기때문에 이를 생략한 것입니다.
ELBO
p(x)를 직접적으로 구할 수 없는 상황에서 lower bound를 최대화하는 방식으로 접근

일반적으로 ELBO는 하한선을 의미해서 작거나 같다는 표시이지만, 현재는 log likelihood에 음수가 붙어있기때문에 반대로 취해져있습니다. 여기서 말하는 log likelihood는 특정 데이터가 모델에 의해서 생성된 확률이므로 높을수록 좋습니다.
ELBO(분수형태의 첫번째 수식)은 분자에 revese process, 분모에 forward process의 식이 나타나있습니다. 즉, reverse process(우리가 학습하고자 하는 부분)이 forward process(원래 부분)을 얼마나 닮는지를 나타내는 것입니다.
→
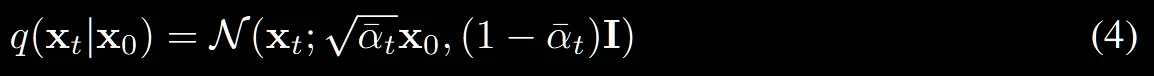
forward process에서 만큼의 노이즈를 추가한다고했는데, 현재의 수식은 에 대해서 나타나있습니다. 입니다.
이렇게 나타낸 이유는 closed form 즉 t시점에 노이즈가 추가된 이미지를 얻기 위해서 한번에 계산하기 위해서, 한마디로 계산의 편의를 위해서입니다.
: t시점까지 노이즈를 모두 곱한 값입니다.
Loss
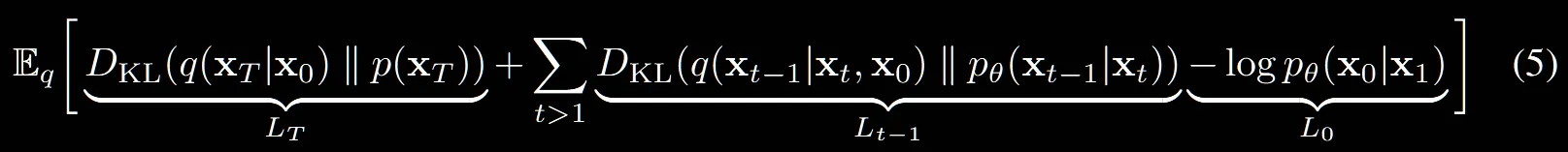
1차 난관입니다. ELBO에서 구했던 수식 L을 수식 (5)와 같이 나타냈다는데 너무 바껴서… Appendix A를 참고해보겠습니다.
참고영상: https://www.youtube.com/watch?v=ybvJbvllgJk&t=514s
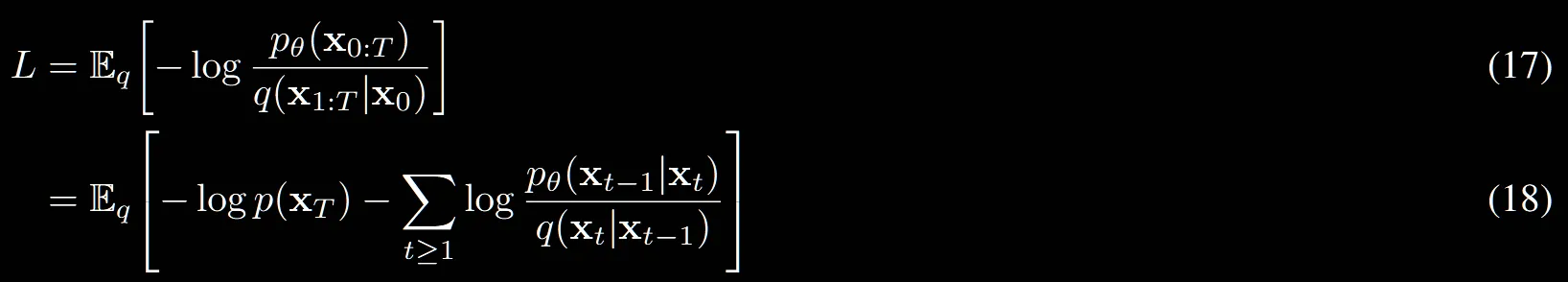
(17) → (18): 자연스럽게 분자의 rever process를 (1)수식의 왼쪽 부분을 가져오면 쉽게 구할 수 있습니다.
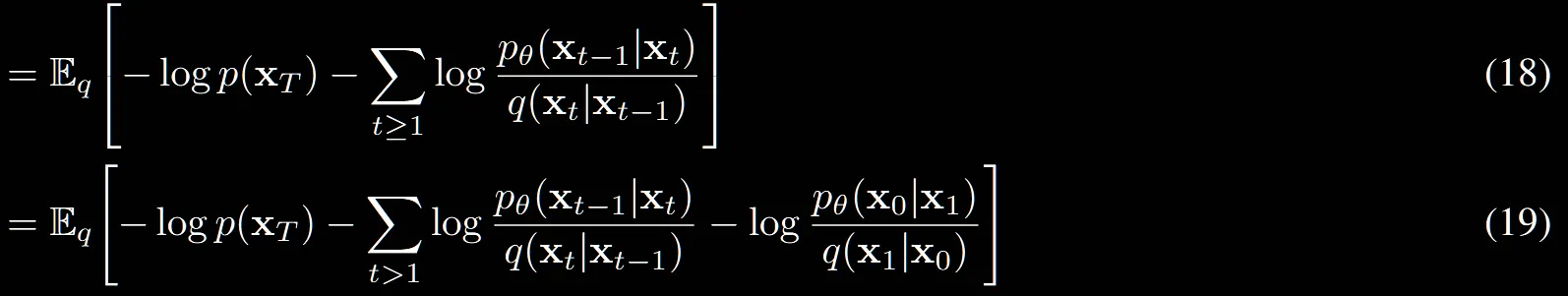
(18) → (19): t=1인경우만 밖으로 빼니까 이부분도 쉽습니다.

(19)→(20): 마의 구간입니다. 자세히 설명해드리도록 하겠습니다.(이해가 안갈시 영상참조)

(19)와 (20)번 수식의 차이는 노란색 부분밖에 없습니다.
[사전개념]
- 마르코프체인: 과거 상태중 직전 상태에만 영향을 받는다
- 베이지안 룰:
[전개 과정]

- 마르코프 체인을 역 이용하자
- 베이지안 룰로 위의 값을 바꾸자
- 분모와 분자에 을 곱해주자
- 첫번재 분수의 분자와 두번째 분수의 분모를 베이지안 룰을 이용해 바꾸자
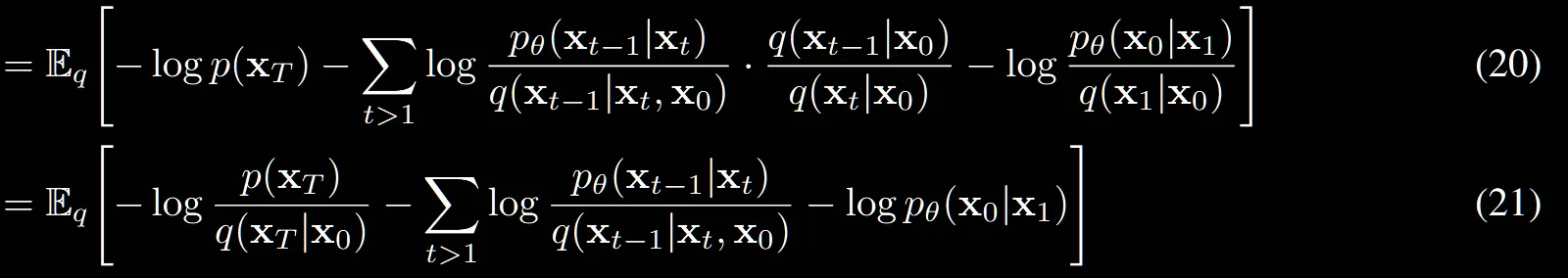
(20)→(21): 두번째 마의 코스입니다.
- log안의 곱셈을 덧셈으로 만든다
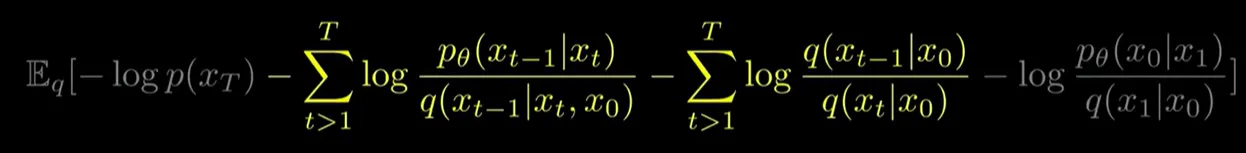
- 오른쪽 수식의 시그마를 다 풀고 약분한다
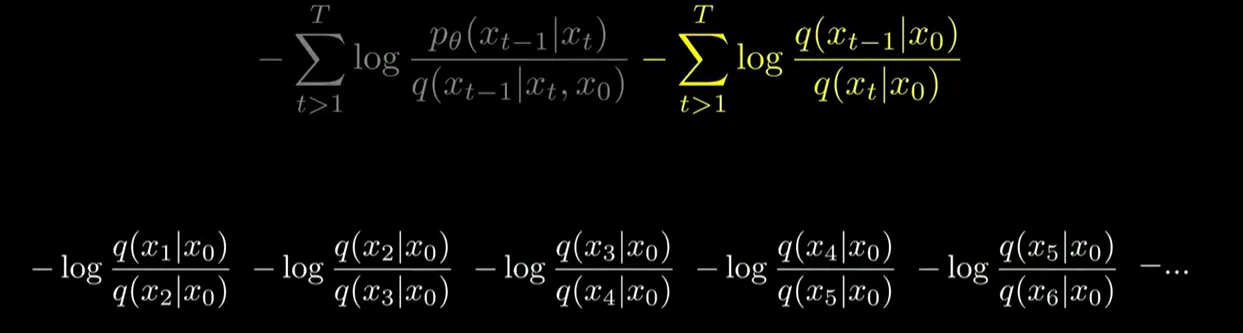
결과:
- 에 대해서 맨 오른쪽 분수의 분모와 약분해주고 는 앞으로 보낸다
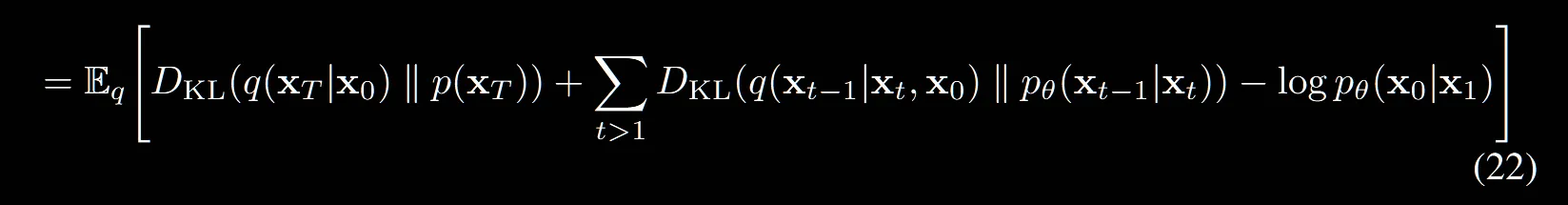
(21) → (22): 마지막입니다!
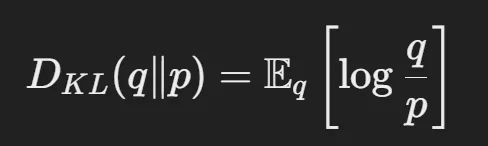
앞의 2개의 텀들을 KL Divergence와 관련된 식이므로 변환하고, 뒤에 부분은 그대로 둡니다.

결론적으로 Loss식은 위와 같은데 마지막 부분의 는 reconstruction term 부분으로 이미지를 생성하는 단계의 Loss입니다.
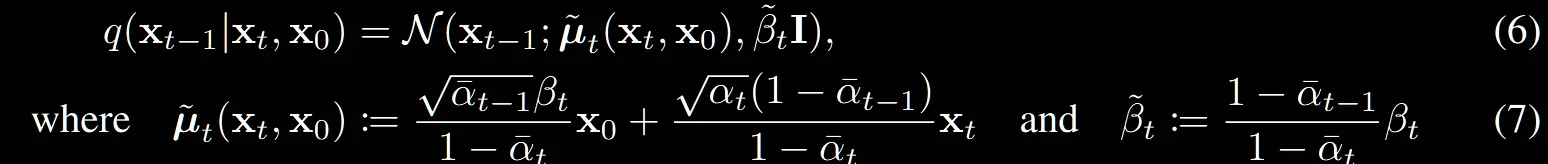
(6), (7) 수식에는 (5)식에서 구한 를 계산하기 위한 방법이 나옵니다.
(6)번식은 평균과 분산을 나타내는 가우시안 분포이고, 와 두분포를 이용해서 구한거니까 두 분포의 합이겠다도 알겠는데 (7) 수식또한 너무 갑작스럽게 나와있습니다.
해당 수식은 https://velog.io/@guts4/Basic-Generative-Model-DDPM의 Denoising Matching Term부분에서 자세히 설명되어있습니다. 간단히 설명드리면 베이지안 룰과 통계에서 배운 평균과 분산의 합을 통해서 구한 값입니다.
Diffusion models and denoising autoencoders
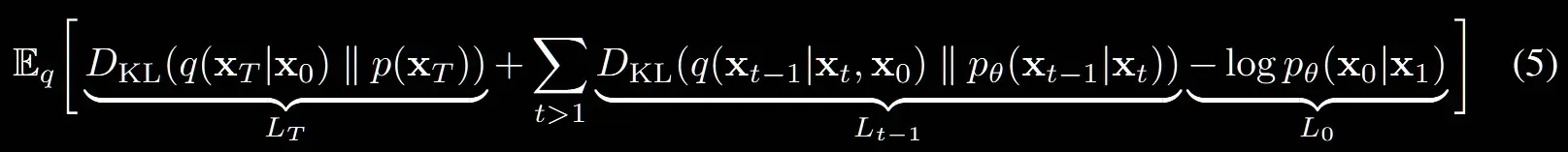
우리가 위에서 정의했던 Loss의 3부분을 각각 어떻게 구하는지 자세히 알아볼 것입니다.
Forward process:
이전에도 설명했지만 forward process는 단순히 정해진 상수를 더하는 과정입니다. 즉 학습하는 과정이 아니기때문에 해당항은 0으로 해서 날려버리게 됩니다.
Reverse process:
지금까지의 설명을 통해서 하나의 step에서 평균과 분산을 예측한다고 했습니다. 하지만 실제로 분산은 고정된 값을 사용한다고 설명했습니다. 이유는 언급하지 않았지만 개인적으로 U-Net이 평균과 분산을 모두 예측하는 것보다는 평균만 예측하는 것이 시간과 성능상 더 좋지 않을까 생각합니다.
그래서 이 고정된 분산을 어떻게 설정할거냐에대해서 첫번째로 고정된 상수를 이용하자, 두번째로 이전에 구할 때 구한 분산을 사용하자 두가지 의견이 나왔습니다. 실험적으로 결과는 비슷했습니다.
고정된 상수는 가우시안 분포에, 두번째 분산은 가 deterministicaally할 때 최적이다라고 표현했습니다. 참고로 여기서 말하는 결정론적이라는 것은 항상 결과가 동일한 경우입니다. 즉 x0가 고양이 사진이면 결과는 항상 고양이 사진입니다.
그러면 은 평균만 예측하는 부분이 되겠는데 어떻게 평균을 예측하는지 알아보도록 하겠습니다.
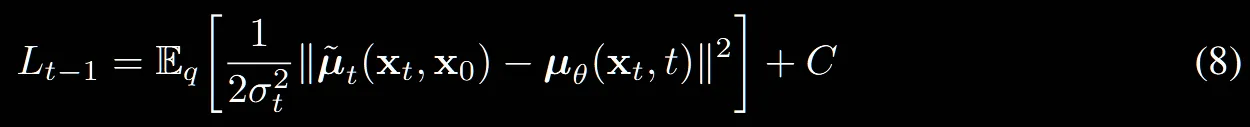
위의 수식에서 우리는 t-1시점의 평균이 라는 것을 확인했습니다. 따라서 t시점으로부터 노이즈를 제거한 t-1시점의 예측한 평균과 t-1시점의 우리가 알고있는 평균의 차이를 최소화하는 것이 Loss부분입니다.
여기서 멈춰도 되지만, 해당 논문에서는 우리가 식(4)에서 노이즈 예측하는 식도 구해놨는데 이거 대입까지해서 더 완벽하게 만들자라는…. 말을 하시면서 아래 수식을 제공해주셨습니다.
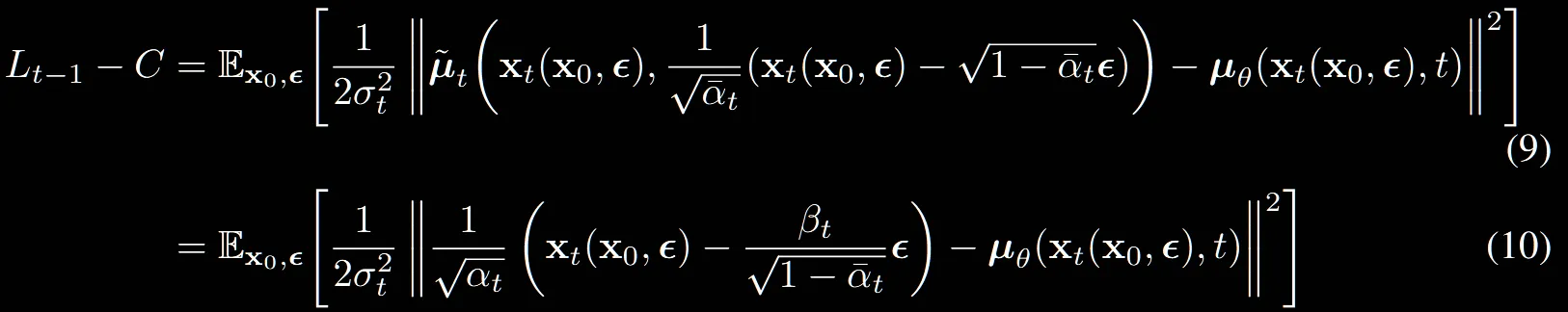
(8) → (9)
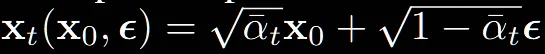
모든 는 로부터 노이즈가 추가된 상태의 이미지이기 때문에 으로 위와 같이 나타낼 수 있습니다.
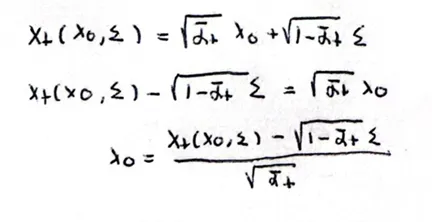
그리고 위의 수식을 에 대한 수식으로 나타내면 (9)번 수식이 나오는 것을 확인할 수 있습니다.
(9)→(10): (9)번에 의 값을 (7번)식에 대입하는 과정

해당 유도과정을 제외하고는 (9)와 (10)의 수식이 동일합니다.
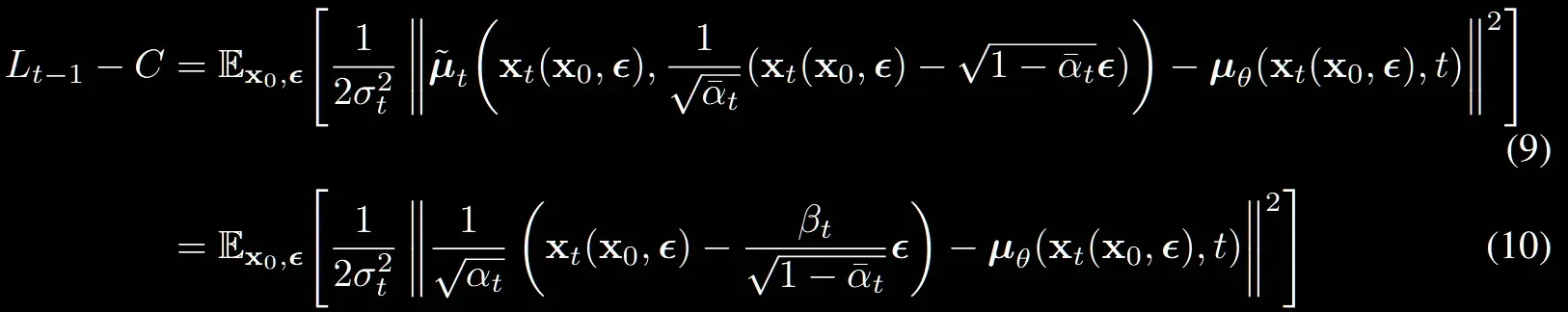
수식 유도과정을 위에서 살펴봤는데 결과를 보면 수식(10)에서 는 를 예측해야되는 것을 알 수 있습니다.
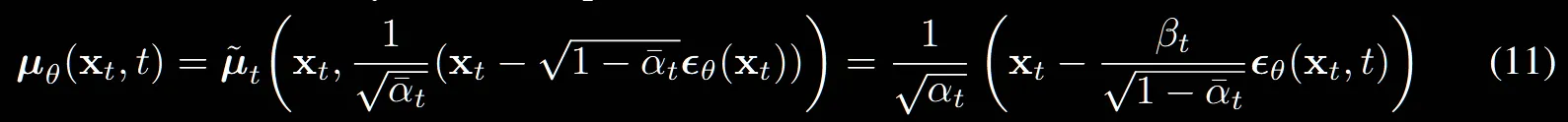
수식(11)은 우리가 t시점의 평균을 예측할 때 실제로는 에 대한 정보가 없으므로, 수식(9)를 유도할 때 했던 방식으로 에 대한 식을 대체하여 에 대입합니다.
여기서 이전의 과 다른 는 t시점의 노이즈를 예측하는 네트워크입니다. 즉 여기서는 평균을 예측하는 것이 아니라 해당시점의 노이즈를 예측하는 과정입니다.
논문에서는 t시점에서의 평균 예측, 노이즈 예측 그리고 마지막으로 예측이 모두 가능하지만 마지막 예측의 성능은 좋지 않다고 밝혔습니다.
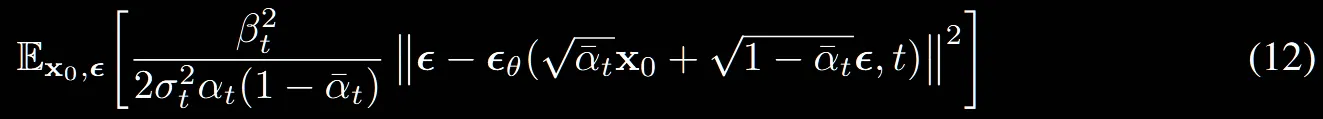
수식(12)는 수식(10)에서 대신에 식을 대입한 노이즈 예측에 대해서 나타낸 수식입니다.

지금까지 설명을 잘 따라와주셨다면 해당 알고리즘은 이해하는데 어렵지 않을 것입니다.
Training: 식(12)에서 가져온 수식을 이용해서 t시점의 노이즈를 예측하면서 학습을 진행합니다.
Sampling: 식(11)에서 가져온 수식을 이용해서 t시점의 노이즈를 제거합니다. 이때의 노이즈는 평균에만 제거하면서 진행됩니다.
Data scaling, reverse process decoder
Data Scaling
이미지의 각 픽셀 값은 {0~255} 사이의 값을 갖고 있습니다. Neural network가 조금더 잘 학습하도록 이를 [-1~1]까지의 값으로 스케일링 하여 학습을 진행하게됩니다.
이때 마지막에 다시 이미지로 복원할 때는 스케일링 값 한것을 반환하는 과정이 필요합니다.
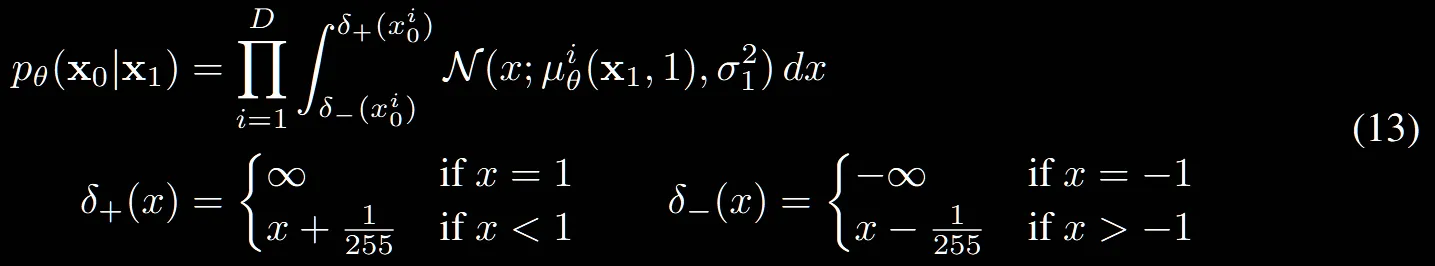
수식(13)이 Scaling의 반환과정에 대한 설명입니다. D는 차원수를 나타냅니다.
적분을 통해서 연속적인 분포에서 이산적인 분포로의 변환을 통해서 이미지의 형태를 잘 나타낼 수 있는 것입니다. 이후 log likihood를 최대화하면서 학습을 진행하게 됩니다.
Simplified training objective
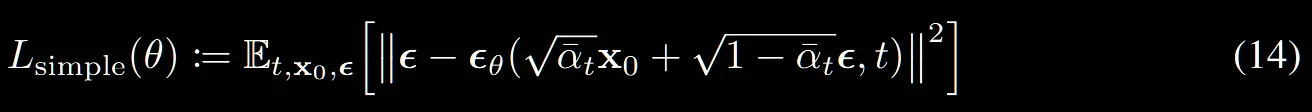
수식(12)에서 앞에 상수를 제거한 간단한 ELBO버전 식입니다. t=1일 때의 수식은 (13)과 같아진다고 보시면됩니다.
Experiments
하이퍼파라미터
- T=1000
- = , linear하게 증가
- 마지막 데이터의 KL Divergence값이 거의 를 나타낸 것으로 보아, 거의 노이즈로만 구성된 것을 알 수 있습니다.
- U-Net backbone
- 16x16 feature map에서 self-attention을 실행
Sample quality
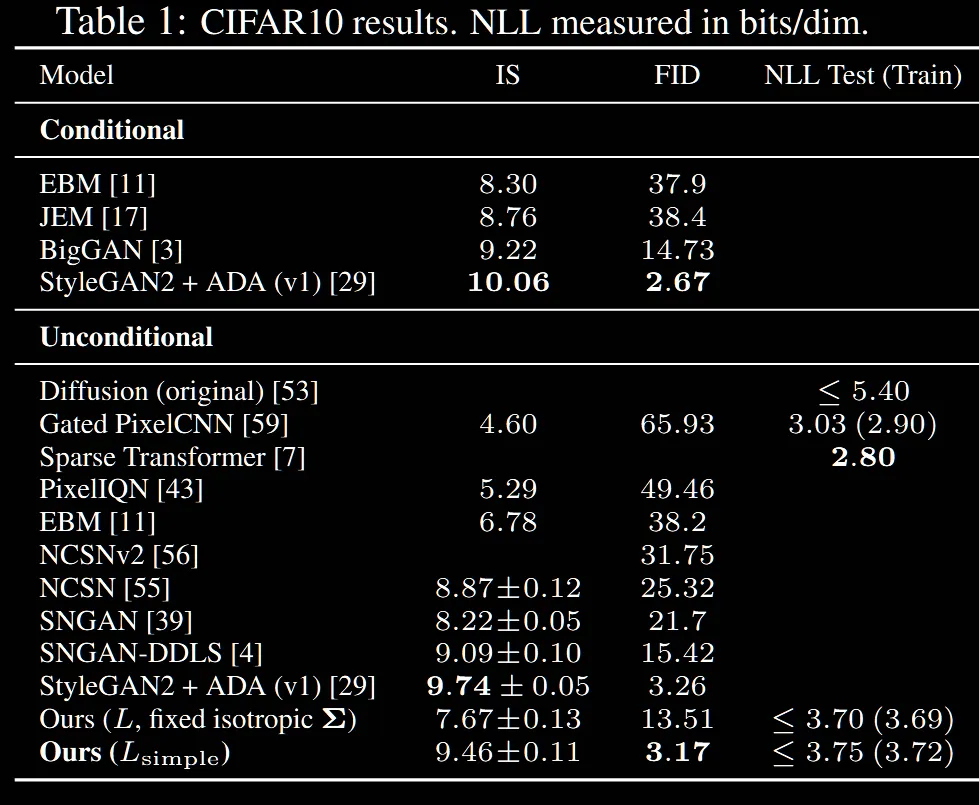
위의 Table1은 Inception socres(IS), FID scores, negative log likelihoods(nll)을 CIFAR10 데이터에 대해 여러 모델들과 비교한 결과입니다.
Inception Score(IS): 생성 모델이 얼마나 다양하고 좋은 이미지를 생성하는지 평가하는 지표입니다. → 클수록 좋다
- Inception 모델이 예측한 클래스의 확률 분포를 기반으로 계산합니다.
- 단 모델의 예측을 기반으로 작동하기 때문에 사람의 비교와는 품질이 다를 수 있습니다.
FID Score: 생성된 이미지와 실제 이미지의 분포 간의 거리를 측정하는 지표로, 얼마나 생성된 이미지가 진짜 같은지를 나타냅니다. → 작을수록 좋다
- 실제 이미지와 생성된 이미지 모두 Inception 네트워크에 통과시켜 특징 벡터를 추출한 후, 두 분포의 평균과 분산 거리를 비교합니다.
- 계산이 복잡하고, 충분히 많은 샘플이 필요합니다.
Negative Log Likelihood(NLL): 모델이 주어진 데이터를 얼마나 잘 맞출 수 있는지 → 작을수록 좋다
- likelihood는 이전에도 설명했지만 데이터를 얼마나 잘생성하는지를 나타냅니다.
- 따라서 음수값을 취한 값이 작을수록 데이터를 잘 설명합니다.
- 직관적이지만, 고차원 데이터의 경우 NLL 계산이 어려울 수 있습니다.
Reverse process parameterization and training objective ablation
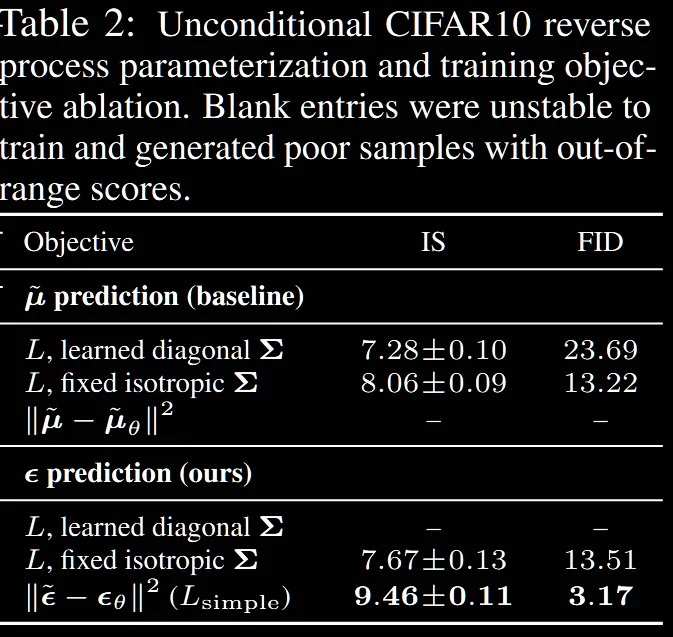
위의 Table2는 이전에 설명한 평균 예측과 노이즈 예측의 결과 차이를 보여주는 표 입니다. 표에서 learned diagonal은 분산을 고정하지 않고 평균처럼 학습했을 때, fixed isotropic은 이전에 설명한것처럼 평균만 학습하고 분산을 고정했을 때의 결과입니다.
결론적으로 노이즈를 예측하는 것중에서도 분산을 고정시킨 모델이 좋고, 이를 식 (12) → (14)처럼 단순화했을 때 성능이 한번더 개선된 것을 확인할 수 있습니다.
Progressive coding
솔직히 처음 보는 내용이라 당황했습니다. 생성모델이 이미지 압축모델로 사용될 수 있다니… 일단 자세히 한번 알아보도록 하겠습니다.
쉽게 말하면 입력 이미지가 가 되어서 이를 Forward Proces

s를 거치면서 로 만듭니다. Forward process를 거치면서 노이즈가 추가되는데 이과정에서 이미지의 중요한 부분과 중요하지 않은 부분을 구분할 수 있고, 다시 Reverse process 과정이 진행될 때 중요한 부분만 복원하면서 이미지를 압축할 수 있는 것입니다.
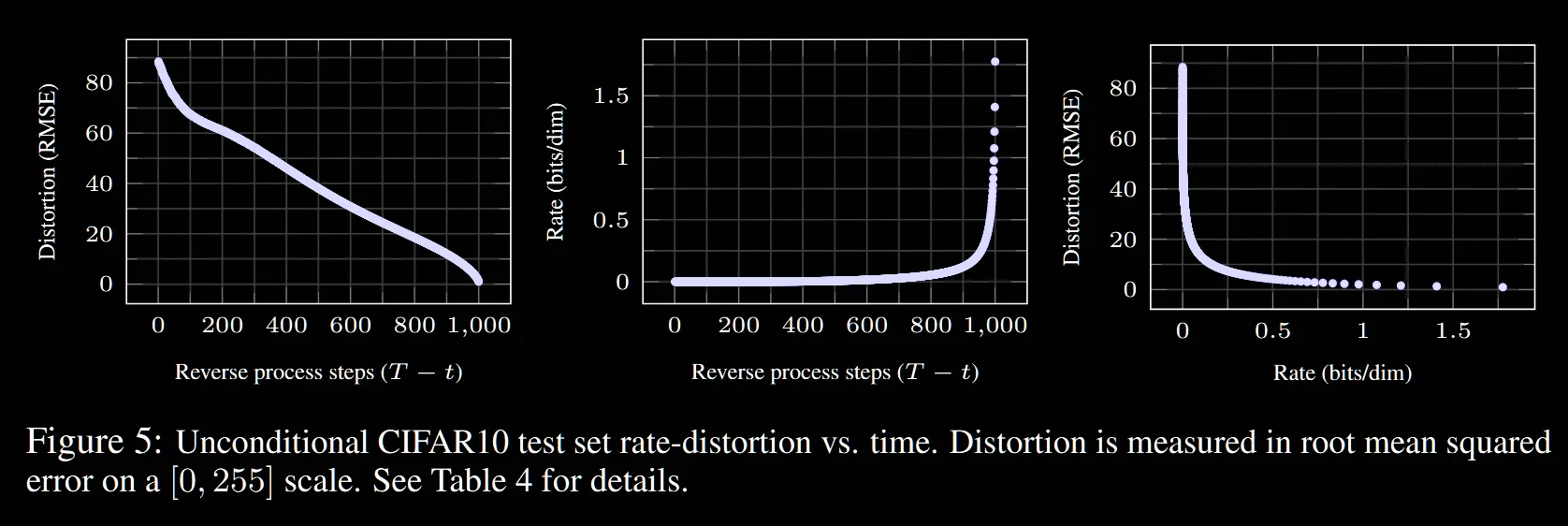
그림은 time step 별로 압축률(rate)와 이미지의 왜곡 정도(Distortion)을 나타냅니다. 초반에 급격하게 왜곡과 압축이 일어나는 것을 확인할 수 있습니다.
Interpolation

해당 과정은 2개의 이미지를 합쳤을 때 결과를 나타낸 것입니다.
왼쪽 사진의 파란색 사진이 입력이미지입니다. 파란색 사진이 2개 즉 입력 이미지가 2개들어가서 이를 T시점의 노이즈값으로 보내면 위의 파란색 2개의 점이 됩니다. 파란색 점 2개를 interpolation을 통해서 초록색 점으로 만들고 다시 이 초록색 점을 reverse process를 통해서 빨간색 이미지로 만드는 과정입니다.
