Generative Modeling by Estimating Gradients of the Data Distribution[1] Yang Song Blog 리뷰
논문 저자 Yang Song님이 정리해주신 내용: https://yang-song.net/blog/2021/score/
생각보다 내용이 글어서 해당 글에서 논문 저자 Yang Song님이 정리해주신 블로그 글을 알아보고, 이후에 논문 리뷰를 진행하도록 하겠습니다.
Introduction
생성 모델은 probability distribution(확률 분포)를 어떻게 나타내는지에 따라서 크게 2가지로 분류 할 수 있습니다.
Maximum likelihood 참조 영상: https://www.youtube.com/watch?v=XepXtl9YKwc
- likehood-based models
데이터의 분포가 확률 밀도 함수 또는 확률 질량 함수로 학습하는 모델. 이 모델은 주어진 데이터가 특정 확률 분포를 따를 가능성을 최적화하는 방식으로 학습
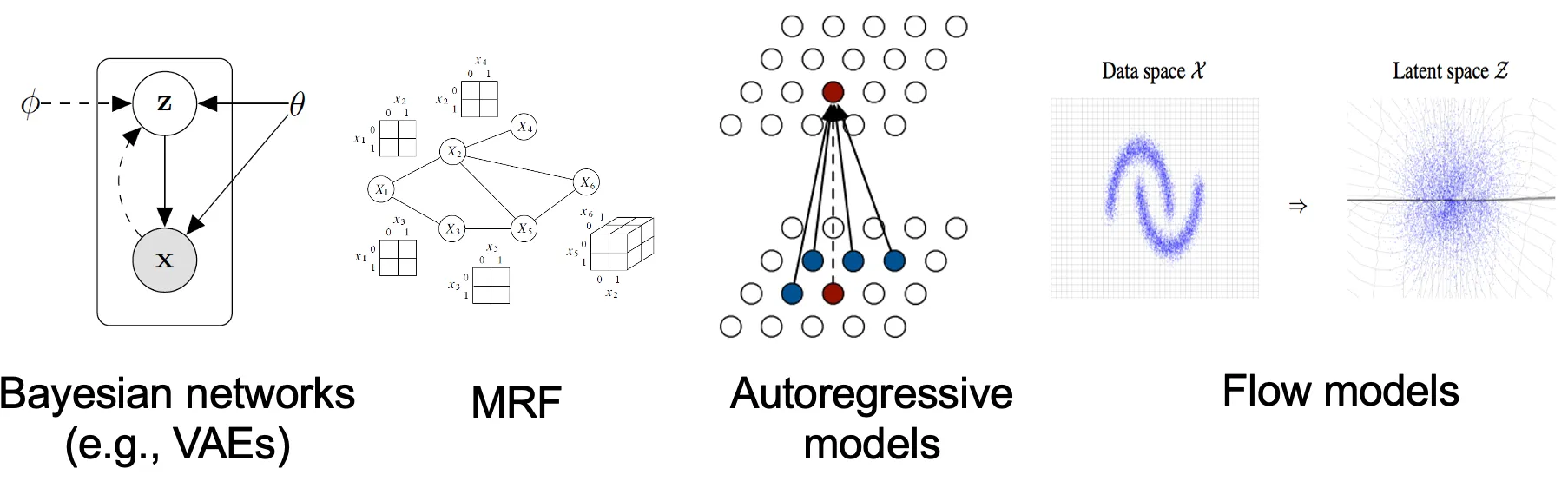
Autoregressive models, normalizing flow models, energy-based models, variational auto-encoders(VAEs)가 likehood-base models에 속해 있습니다.
- implicit generative models
probability distribution을 명시적으로 모델링 하지 않고, 샘플링 과정을 통해 데이터를 생성하는 모델이 implicit generative model입니다.
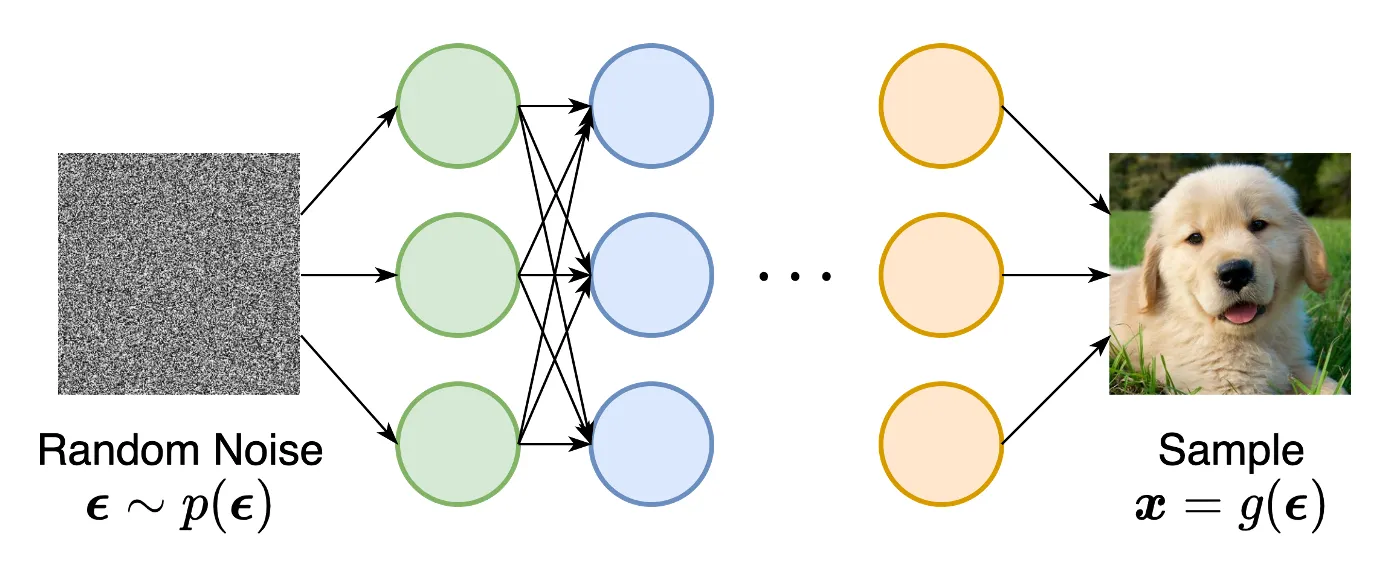
대표적인 모델은 GAN이 있습니다. 랜덤 가우시안 벡터를 입력받아서 이를 Neural network를 통해서 변환하는 과정입니다.
위의 2가지 모델들은 한계점들이 존재합니다. 우선 likehood 기반 모델에서는 normalization constant(정규화 상수)를 구하는데 많은 연산량이 필요해서 모델 구조에 대해서 제한을 준다거나, surrogate objectives(대체 함수)를 이용합니다. Normalizing constant를 구하는게 힘든 이유는 정규화를 위해서 모든 벡터의 합을 구해야하는데, 이때 고차원 벡터를 적분할 때 매우 많은 연산량이 필요하기 때문입니다.
다음으로 implicit generative models중 하나인 GAN에서의 대표적인 문제인 unstable한 문제과 mode collapse(다양성 부족) 현상이 나타납니다. Discriminator를 속이기만 하면 된다는 생각에 Generator가 생성하는 이미지의 범주가 작아지게 되는 것입니다.
해당 블로그에서는 이전 확률분포의 한계를 극복하는 새로운 방법을 설명합니다. 핵심 아이디어는 log probability density function의 gradient 즉 score function 을 이용하는 것입니다. Score 기반 모델들을 사용하면 이전 liklihood 기반 모델의 단점인 정규화 상수를 계산할 필요가 없어지게 됩니다.
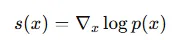
Score function은 위에 있는 수식처럼 나타낼 수 있습니다. 로그를 취한 이유는 gradient 즉 미분이 가능한 형태로 변형하기 위해서 이고, gradient을 이용해서 점진적으로 pdf를 구해나가는 과정입니다.
normalizing flow model 설명: https://jaeseongyou.wordpress.com/2020/05/04/%ec%a0%95%ea%b7%9c%ed%99%94-%ed%94%8c%eb%a1%9c%ec%9a%b0-%ed%8a%9c%ed%86%a0%eb%a6%ac%ec%96%bc-%ed%8c%8c%ed%8a%b81-%eb%b6%84%ed%8f%ac%ec%99%80-%ed%96%89%eb%a0%ac%ec%8b%9d/
자세한 사항은 위의 한국어 설명을 보시면 되고, 간단하게 요약하자면 복잡한 분포를 간단한 분포로 변환해주는게 normalizing flow model의 역할입니다.
조금더 간단하게 영상으로 보시고 싶은 분들은 https://www.youtube.com/watch?v=SuRML3Aj4m0 링크를 참고하시면 좋을거같습니다.
The score function, score-based models, and score matching
참고 영상: https://www.youtube.com/watch?v=d_x92vpIWFM 해당 영상에서 score-based model에 관한 기본적인 설명이 잘 나와있어서 참고하면 좋을거같습니다.
몇개의 데이터셋 이 주어졌을 때 생성 모델은 이를 기반으로 데이터 포인트를 샘플링해서 새로운 이미지를 잘 생성해야 됩니다.
데이터 포인트를 잘 샘플링 하기 위해서는 데이터의 분포가 잘 생성되어야겠죠? 우리가 학습하고자 하는 데이터 분포를 라고 했을 때 이를 학습시켜주는 모델을 라고 정의하겠습니다.
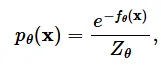
그러면 수식은 위와 같은 형태가 나올 것입니다. 이때 은 normalizing constant로 의 적분 결과가 1이 나오도록 하는 값입니다.
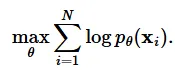
학습은 Maximum likelihood 방식으로 진행됩니다. 위의 식이 성립하기 위해서는 확률의 합이 1이라는 조건을 만족해야하는데 그러기 위해서는 이전에 설명한 가 필요합니다. 하지만 이를 계산하는게 매우 복잡하고 이 문제는 introduction의 likehood-based model에서 알아본 사실입니다.
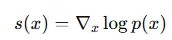
이러한 문제를 해결하기 위해서 나온 개념이 score function입니다. score function은 로 나타내기로 하고 수식은 위와 같이 나타낼 수 있습니다.
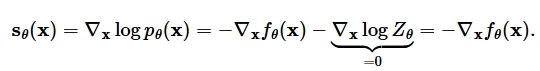
이전식의 p(x)에 energy-based model에 관한 첫번째 식을 대입하면 상수가 날라가고 최종적으로 오른쪽 식이 나오는 것을 알 수 있습니다.
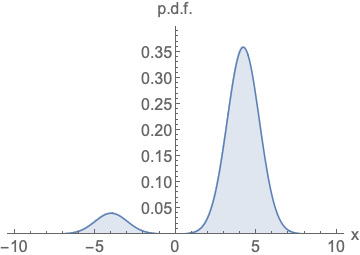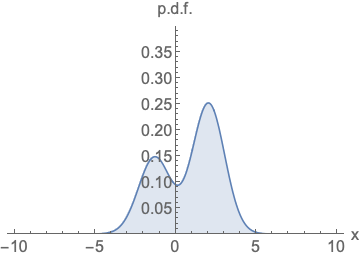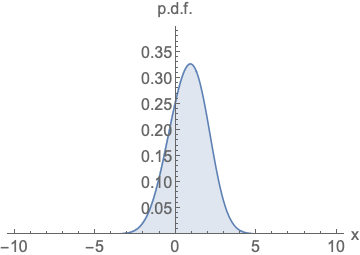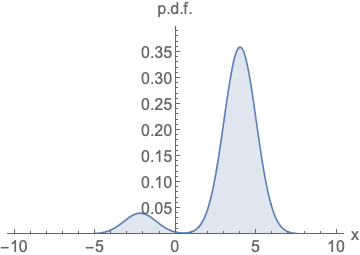
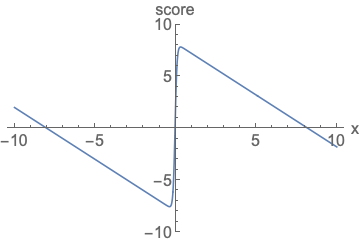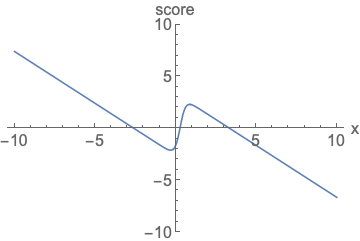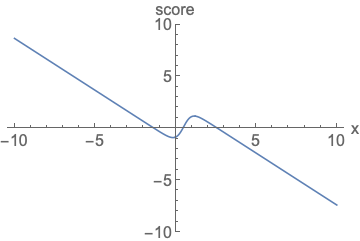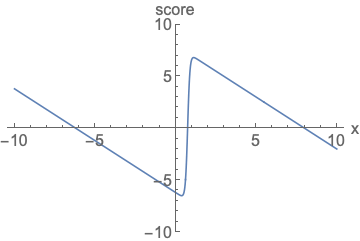
왼쪽 확률 밀도 함수는 넓이가 1이 되기 위해서 정규화를 진행해야하고, 오른쪽 score function은 정규화 없이 값을 나타낼 수 있음을 시각화 한 것입니다.
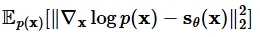
likelihood-base model과 비슷하게 Fisher divergence로 데이터의 분포를 학습할 수 있습니다. Fisher divergence는 2개의 분포를 L2 distance를 이용해서 거리를 최소화하는 방식으로 학습이 진행됩니다.
하지만 우리는 아쉽게도 데이터의 분포 p(x)를 저희는 알지 못합니다. 다행히 score matching이라는 방식을 이용해서 Fisher divergence를 구할 수 있는 방법이 나타나있습니다.
사용에 있어서 큰 제약조건들은 없지만, 입력과 출력의 차원이 동일해야한다는 사소한 제약조건은 존재합니다.
Langevin dynamics

Score function을 학습한 후 Langevin dynamics를 통해서 Sampling을 진행할 수 있습니다.
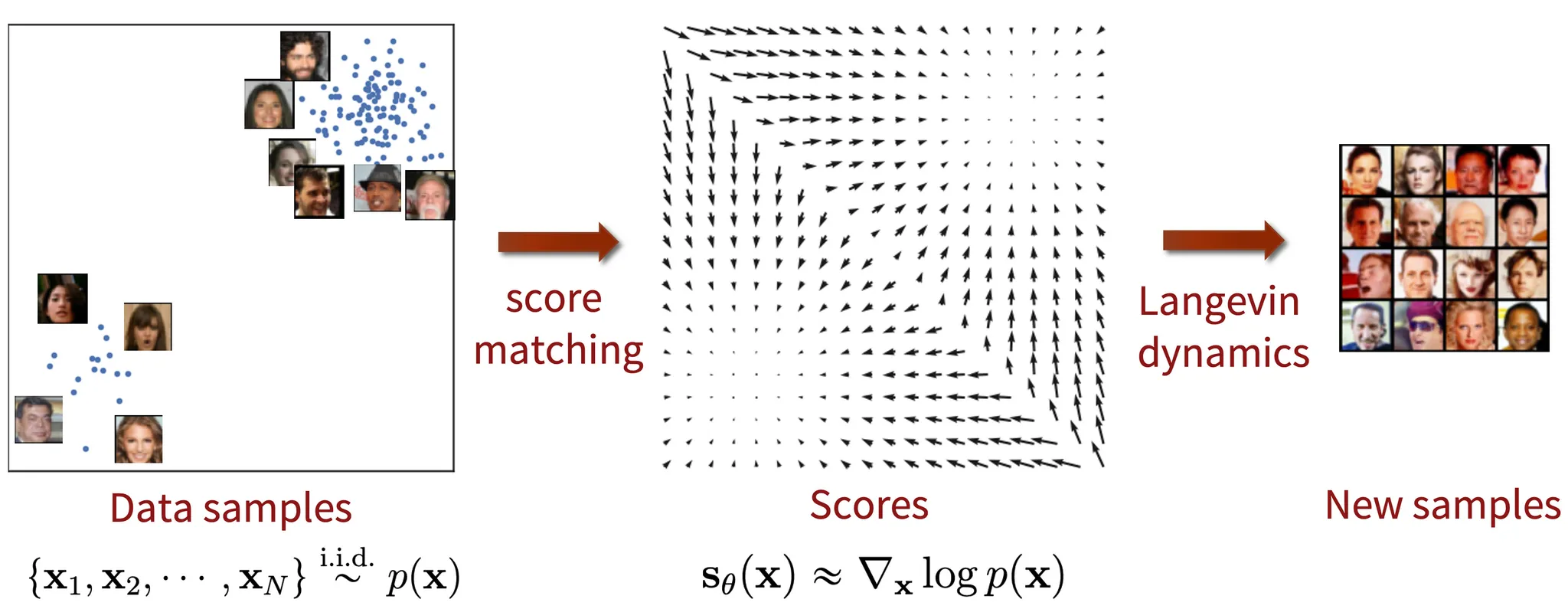
화살표가 Score function 즉 해당 시점에서 확률 분포의 이동 방향을 나타내고, 위의 수식을 보면 이전단계에서 화살표 방향만큼 더한 값이 현재시점이라는 것을 쉽게 알 수 있습니다. , 이면 무시할만한 오차만 생긴다고 합니다.
Naive score-based generative modeling and its pitfalls
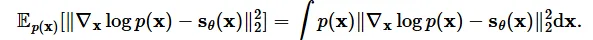
지금까지 score matching을 이용해서 어떻게 score function을 학습시키는지와 Langevin dynamics를 이용해서 어떻게 샘플을 생성하는지 알아봤습니다. 하지만 이러한 naive(순진한) 접근은 제한적인 성공을 가져옵니다. 이제부터 score mathing의 pitfall(함정)에 대해서 알아보도록 하겠습니다.
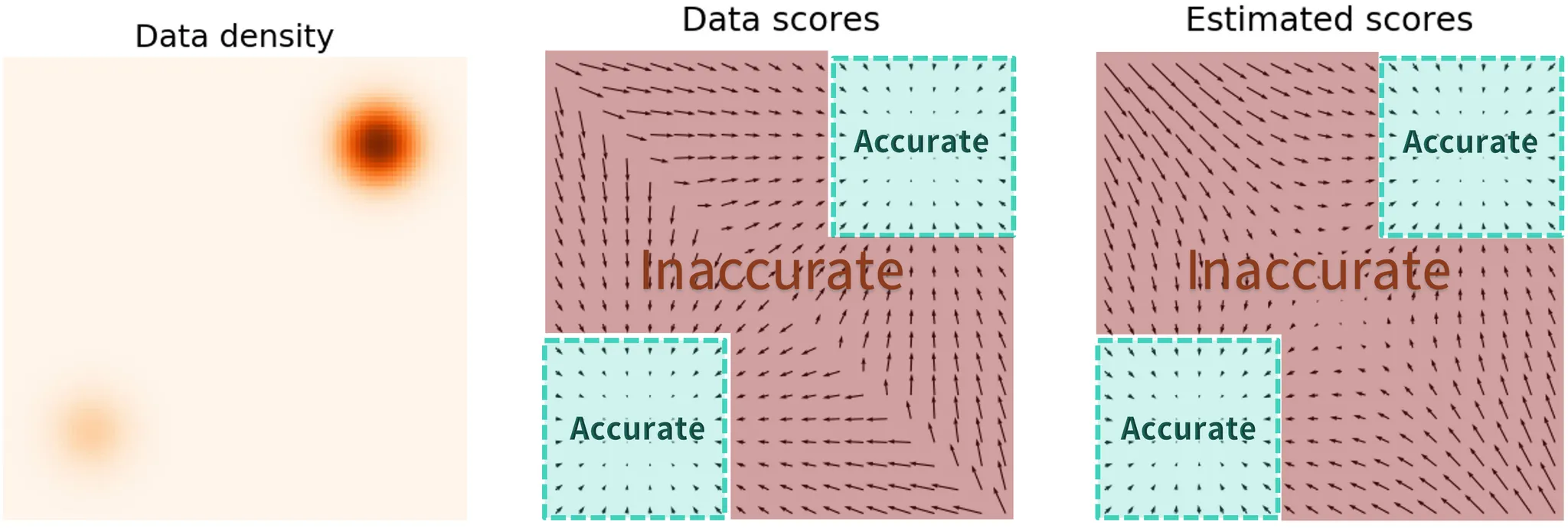
위의 수식은 score function을 구하는 방법인데, p(x)가 작은 부분은 위의 수식의 값이 작아져서 loss를 계산할 때 무시하게 됩니다. 따라서 해당 영역에 대한 부정확한(inaccurate) 결과가 나오게 됩니다. 아래 그림은 이를 시각화 한 것입니다. 데이터 밀도가 높은 즉 p(x)가 큰 부분은 정확한 결과를 나타내지만, 데이터의 밀도가 작은 즉 p(x)가 작은 부분은 부정확한 결과가 나옵니다.

따라서 초기 샘플이 low-density region에 위치할 경우 Langevin dynamic가 제대로 학습하지 못하고, 좋지 않은 결과가 생성될 것입니다.
Score-based generative modeling with multiple noise perturbations
어떻게 하면 low-density region에 대해서도 잘 학습할 수 있을까요? 바로 노이즈를 추가해서 데이터에 혼동을 주는 방법을 사용했습니다. 데이터에 노이즈가 추가되면 high-density region에 있는 데이터들이 low-density로 이동할 수 있기 때문입니다.
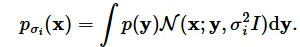
그러면 어떤 noise scale을 추가해야할까요? 큰 값일 경우 low density region으로 이동이 많아져서 이전의 한계를 극복할 수 있지만 원래 데이터의 분포를 망칠 수 있습니다. 작은 노이즈는 반대로 이러한 붕괴 현상은 막을 수 있지만 이전의 low-density의 분포를 학습하는데는 제한적일 것입니다.
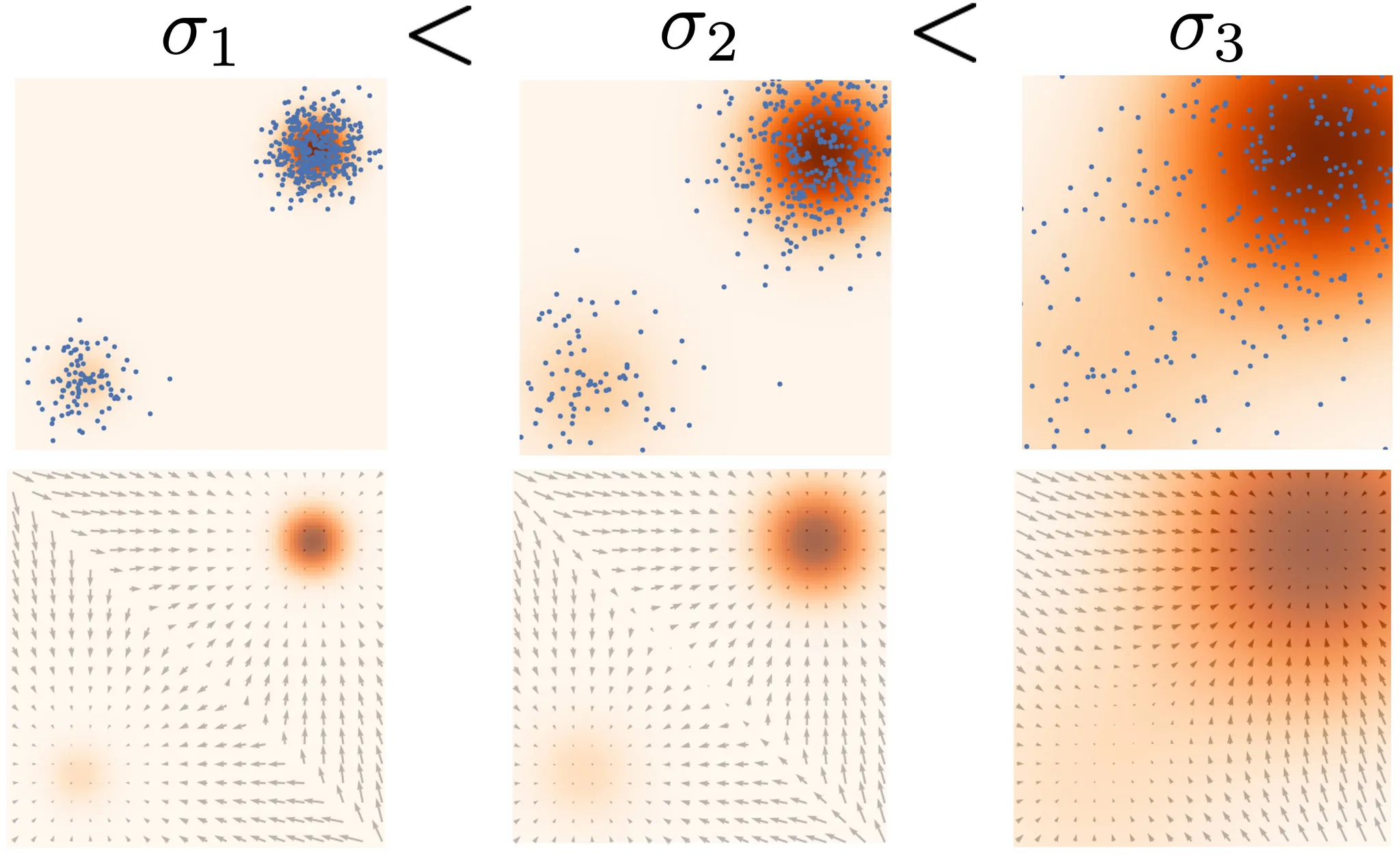
따라서 multiple scale로 노이즈를 동시에 추가했습니다. 의 값은 시간이 지날수록 점점더 작아질것입니다. 이러한 방식을 Noise conditional Score-Based Model 라고 합니다(또는 Noise Conditional Score Network(NCSN)).
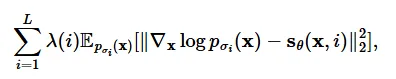
는 Fisher divergnce의 모든 노이즈 스케일의 weighted sum을 통해서 학습합니다.
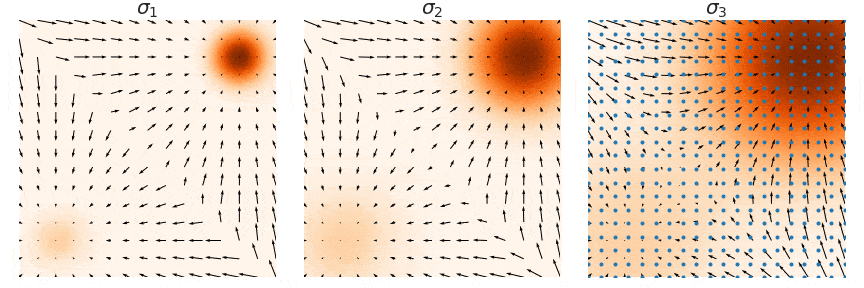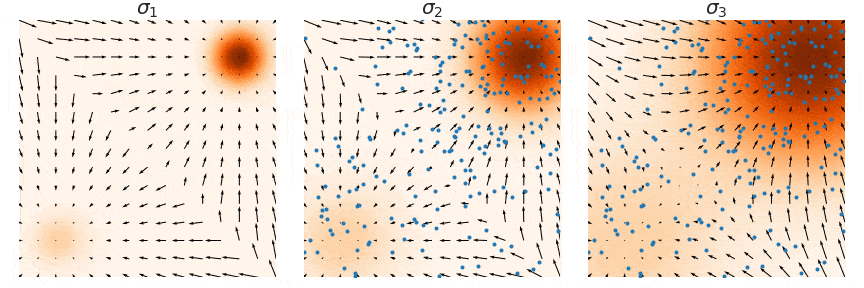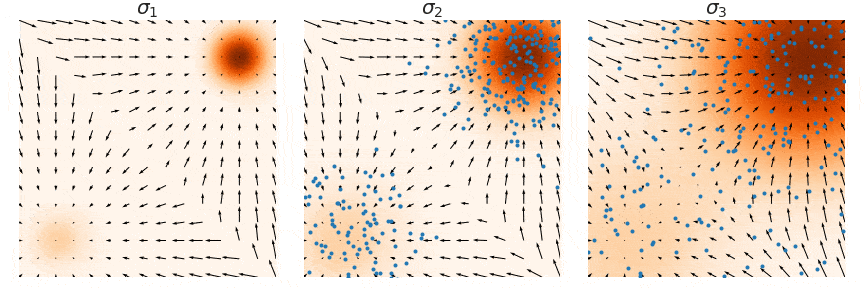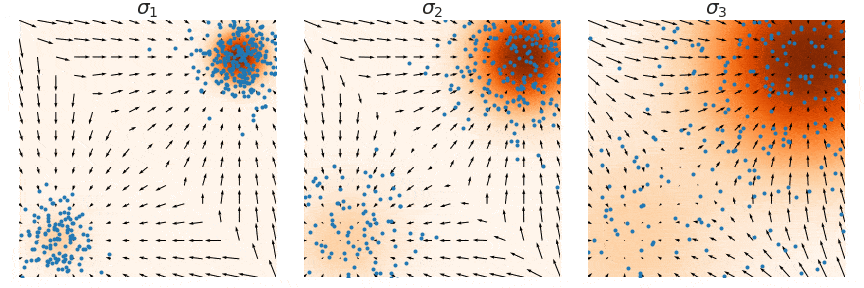
이제 최종적으로 위와 같이 학습된 score-based model 를 이용해서 annealed Langevin dynamics를 진행합니다. score function에 i값이 추가되었기 때문에 i값을 L~1까지 점점 줄여가면서 sampling 과정을 진행하는 것입니다.

실제로 CIFAR-10 데이터를 NCSN 모델을 이용해서 얻은 결과입니다.
Score-based generative modeling with stochastic differential equations (SDEs)
노이즈를 여러번 더하는 것은 score-based generative model의 핵심 성공 방법입니다. 노이즈를 더하는 과정을 많이 진행할수록 이미지 퀄리티는 높아질 것이고, log-likehood계산과 inverse problem을 푸는데 더 수월해질 것입니다.
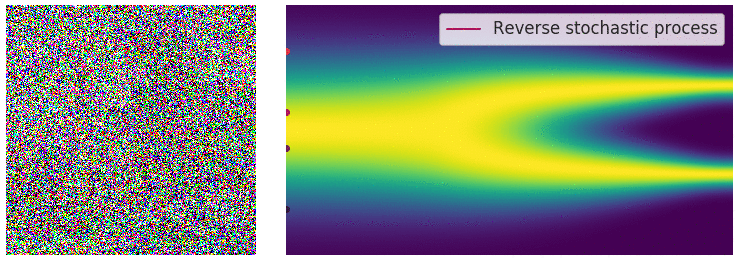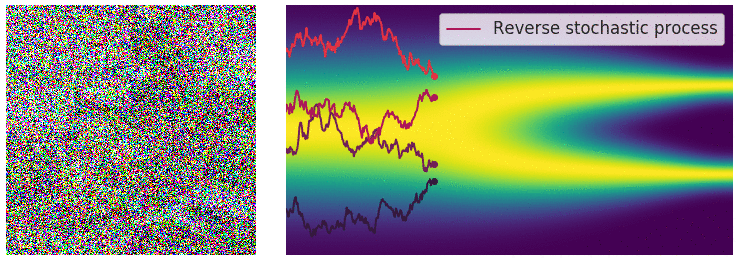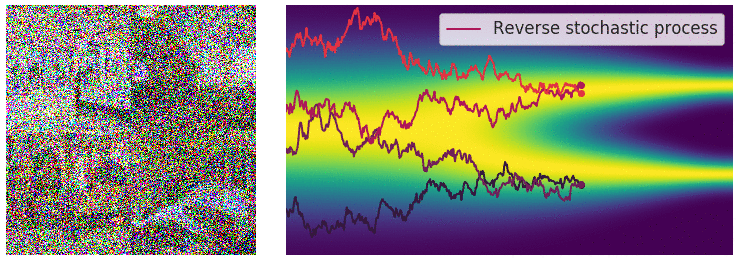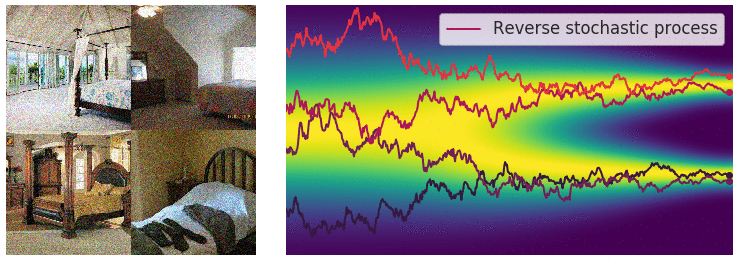
노이즈를 여러번 더한다는 과정을 조금 더 자세히 적자면, 노이즈를 더하는 과정을 불연속적인 과정에서 연속적으로 변환시키자는 것 입니다.
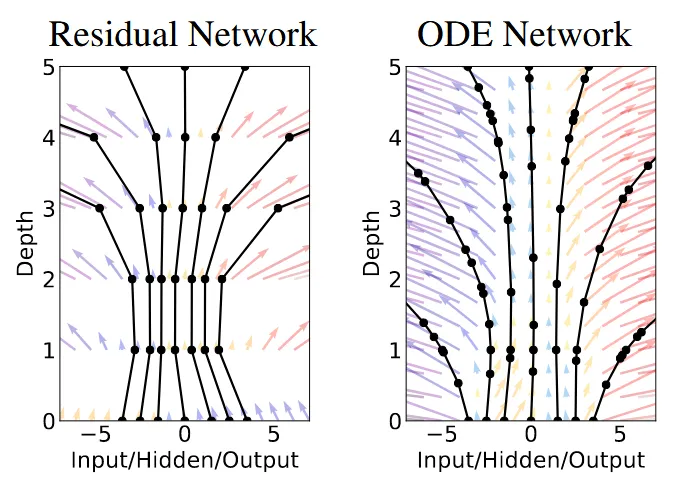
해당 그림은 Neural ODE에서 가져온 그림입니다. 왼쪽이 ResNet의 Vector field, 오른쪽이 ODE의 Vector field입니다. 왼쪽은 확실히 layer(depth)마다 단절되어있다는 느낌이 있고, 오른쪽은 화살표가 끊임 없이 연결되어있는 것을 볼 수 있습니다.
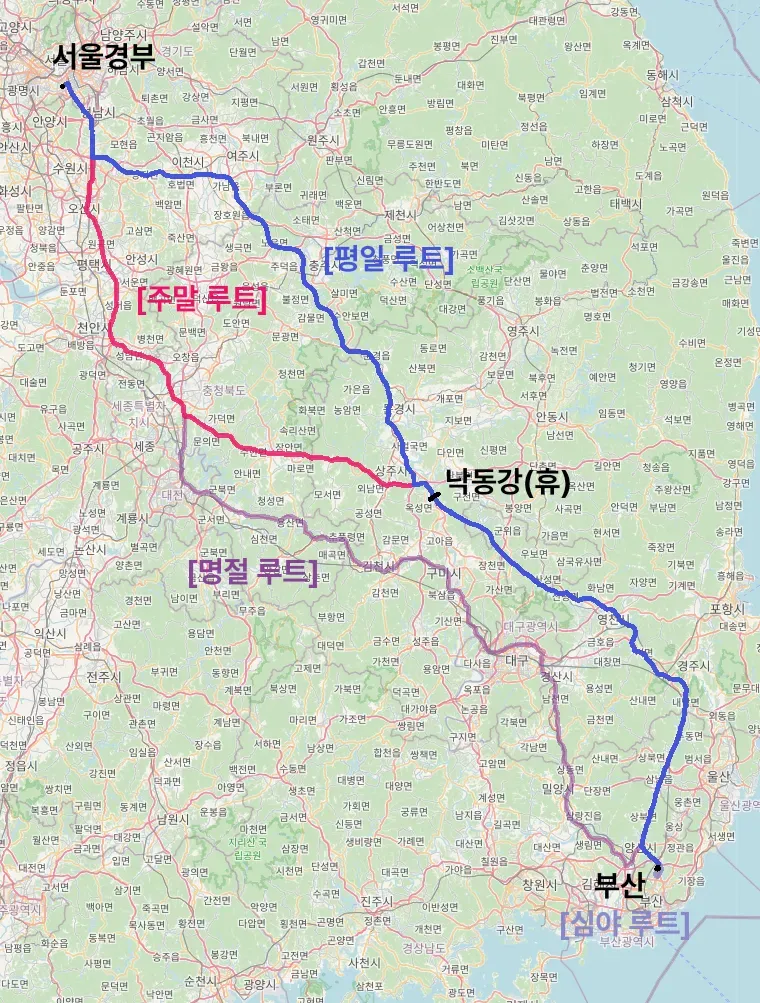
그러면 왜 이렇게 discrete한 모델을 continous하게 만들까요? 예를 들어서 서울에서 부산까지 가는 길을 찾는다고 가정해보겠습니다. 만약에 중간에 천안 휴게소를 들렸다 가세요 했을 경우, 기사님들마다 그리고 교통 혼잡도에 따라서 다양한 경로가 생성될 수 있습니다. 하지만 만약에 중간에 이천을 찍고, 여주쪽으로 와서 종각을 거쳐서… 이런식으로 많은 중간 지점들을 지정해준다면 경로는 [평일 루트]로만 선택될 것입니다. 이처럼 중간에 많은 제약조건을 주는 방법이 continous하게 하는 방법과 유사하게 중간중간 계속 ground truth와 비교해서 정확한 경로를 찾을 수 있습니다.
결론적으로 continous 모델이 성능이 더 좋아서 이를 선호하고, 구현하기 위한 방법으로 stochasic process를 가져온 것입니다. Stochasic process는 Stochastic Differential Equation(SDE)를 통해 수학적으로 표현할 수 있습니다.
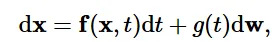
위의 수식이 SDE입니다. 왼쪽의 f(x,t)부분이 Drift coefficient로 상태(x)와 시간(t)에 따라 변화하는 벡터 함수로, 데이터가 어떻게 이동(drift)하는지를 결정합니다. g(t)는 diffusion coefficient로 노이즈가 얼마나 강하게 데이터를 확산시키는지를 제어합니다. dt는 아주 작은 시간의 변화량을, dw는 브라운 운동의 작은 변화량을 나타냅니다.

브라운 운동을 간략하게 설명하면 물리적으로 작은 입자가 액체 속에서 무작위로 움직이는 현상을 나타내는 것입니다. 즉 dw는 시간에 따라서 추가되는 노이즈라고 보시면됩니다.
f(x,t)dt부분만 있다면 x의 변화량은 노이즈가 포함되지 않아서 deterministic합니다. 예를들어서 가속도가 0인상황에서 속도는 변하지 않습니다. 하지만 오른쪽 g(t)dw라는 노이즈가 추가되었고 이때문에 x의 변화량은 예측이 불가능하게 됩니다. 이러한 경로를 stochastic trajectory라고 합니다.
내용이 조금 샌거같은데 돌아와서 우리는 continous하게 노이즈를 무한대로 더하고 싶어서 SDE라는 개념을 가져왔습니다. 사실 위에 나온 SDE는 사용자가 설계한 것입니다.
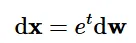
SDE를 설계하는 방법은 여러가지가 존재할 것이고, 위의 수식은 새로운 SDE의 예입니다. 이 SDE는 시간(t)에 따라 점점 커지는 분산을 가진 가우시안 노이즈를 더하도록 설계했습니다.
결론적으로 해당 논문에서는 3개의 SDE를 제시했습니다. 1. Variance Exploding SDE(VE SDE) 2. Variance Preserving SDE(VP SED) 3. sub-VP SDE 추후 3개의 SDE를 자세히 다루도록 하겠습니다.
Reversing the SDE for sample generation
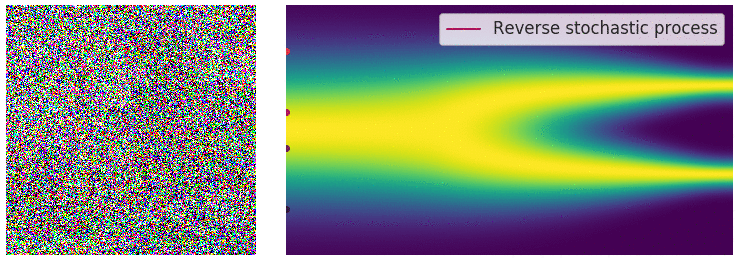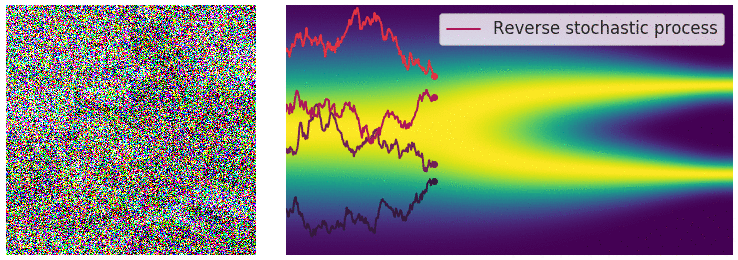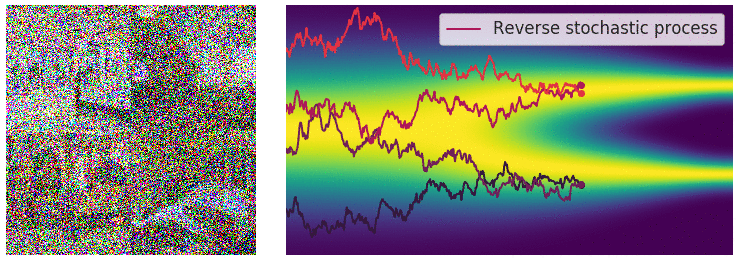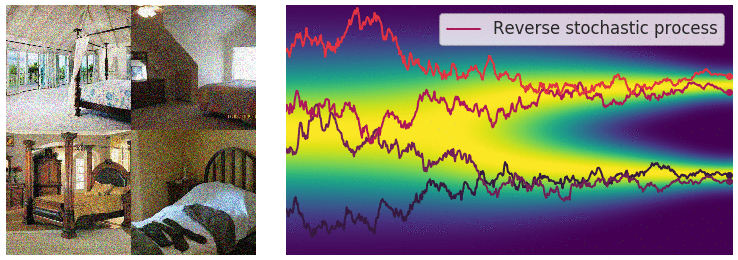
위에서 불연속적인 process사용할 경우 annealed Langevin dynamics를 이용해서 sampling을 진행했었습니다. Continous한 지금의 경우 이와 유사하게 reverse SDE를 통해서 sampling을 진행할 수 있습니다.
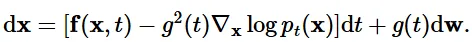
Reverse SDE의 수식은 위와 같습니다. 여기서 주의할점은 reverse기 때문에 dt가 tim step(T→0)의 변화가 반대 방향으로 변하므로 negative infinitesimal time step로 정의됩니다. 노이즈를 제거하기 위해서 이전에 배웠던 score function을 사용하고 forward process에서 scale factor로 사용한 g(t)가 분산으로 작용했기 때문에 제곱해서 scale 값으로 이 된것을 확인할 수 있습니다.

Estimating the reverse SDE with score-based models and score matching
Reverse SDE를 풀기 위해서는 terminal(T시점)의 분포 와 score function 을 알아야합니다. Terminal distribution은 가우시안 분포와 같이 tractable(다루기 쉬운) 초기 조건으로 설정합니다. Score function을 구하기 위해서는 Time-Dependent Score-Based Model 를 구합니다. 이는 이전에 사용한 불연속적인 score-based model을 시간 축으로 확장한 것입니다.
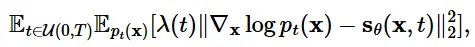
우리의 목적 함수 는 시간적으로 가중합된 Fisher divergence에 의해서 Score function 에 근사하도록 학습됩니다. 위의 수식에서 대부분은 아실텐데 가중치 함수λ(t)는 Score Matching의 손실의 크기를 조정하는 역할을 합니다.
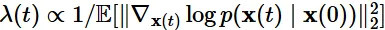
수식은 위와 같습니다. 직관적으로 설명드리면 score function은 초기시점으로 갈수록 작아지고(화살표 크기가 작아짐), T시점으로 갈수록 커지는 것을(화살표가 커짐) 직관적으로 이전 그림을 통해서 알 수 있었습니다. 따라서 이러한 크기 영향을 줄이기 위한 가중치 함수를 설계한 것입니다.
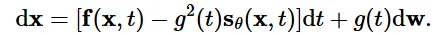
결론적으로 우리가 구하기 힘든 score function대신 를 학습하는 형태로 진행됩니다.
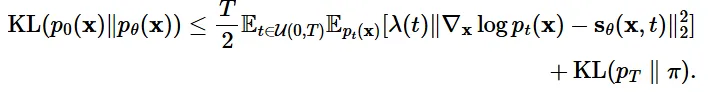
만약에 와 같아진다면 Fisher divergence와 KL divergence의 식은 같아질 것입니다. 해당 과정은 완벽하게 이해는 안갔지만 직관적으로 KL divergence가 와 의 socre function을 비교하는 것이고, Fisher divergence도 를 score function으로 바꾸면 의 score function과 동일하기 때문에 두 식은 같다고 볼 수 있습니다. 더 중요한 것은 KL divergence를 최소화하는 것은 likelihood를 최대화하는 것이랑 같은 의미이기때문에 Fisher divergence의 수식은 높은 lielihood의 결과를 얻을 수 있게 됩니다. KL divergence의 최소화와 likelihood의 최대화도 직관적으로 2개의 분포가 동일해야 KL divergence는 작아지고 likelihood는 커지므로 이해할 수 있습니다.
How to solve the reverse SDE
SDE를 푸는 가장 쉬운 방법은 아마도 Euler-Maruyama method 일 것입니다. Euler-Maruyama method를 사용한다면 결정론적인 부분(f)와 Gaussian noise(g) 부분으로 이산화 될 것입니다.
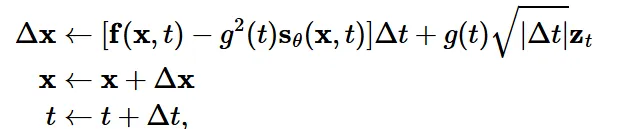
아주 작은 time step동안 2부분으로 나눠서 진행되게 됩니다. Langevin dynamics와 비슷하게 score function을 기반으로 업데이트 됩니다.
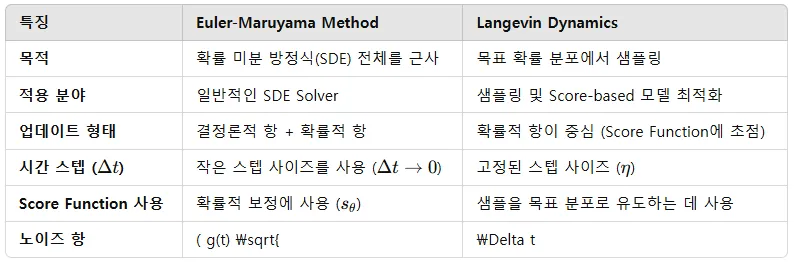
개인적으로 SDE solver에서 사용되는 Euler-Maruyama method랑 Langevin Dynamics의 차이점을 명확하게 하기위해서 정리한 차이점입니다.
Euler-Maruyama 방법 말고도 다른 SDE solver를 이용할 수 있습니다. 예를 들어서, Milstein method, stochastic Runge-Kutta method 방법이 있습니다.
Reverse SDE는 2가지 중요한 속성을 갖습니다.
- 우리는 의 예측을 통해서 를 추정할 수 있습니다.
- 각 시간 단계 에서 독립적으로 샘플링 가능하다.
2가지 속성을 기반으로 Predictor-Corrector samplers를 제안했습니다.
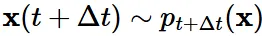
Predictor는 numerical SDE solver의 trajectory(궤적)을 예측합니다.
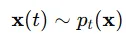
Corrector는 MCMC(Marcov Chain Monte Carlo) procedure를 사용해 보정합니다. 즉 샘플을 미세 조정하여 목표 분포로 더 잘 정렬되도록 합니다. (ex. Langevin dynamics)
정리하자면 큰 궤적을 Predictor를 이용해서 얻게 되고, Corrector를 통해서 이를 세분화하는 작업을 진행합니다.
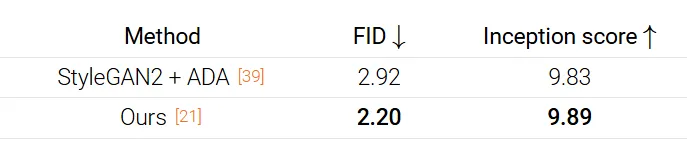
Predictor-Corrector 방식을 통해서 SoTA 모델을 달성할 수 있다고 언급했습니다.



Probability flow ODE
MCMC와 SDE Solver를 이용해서 고화질 샘플들을 얻을 수 있지만, 정확한 log-liklihood는 얻을 수 없습니다.
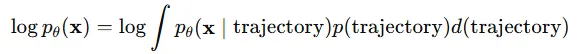
일반적인 log-liklihood의 식은 위와 같은데, SDE의 경우 diffusion항이 존재해서 trajectory가 무한개 존재합니다. 따라서 정확한 log-liklihood를 얻을 수 없습니다.
따라서 Ordinary Differential Equations(ODEs)를 이용해서 정확한 likelihood를 계산할 수 있도록 합니다. Marginal distribution 를 바꾸지 않고 SDE를 ODE로 바꿀 수 있습니다. SDE에 대응되는 ODE는 probability flow ODE라고 불립니다. Marginal distribution을 바꾸지 않는 다는 것은 초기 가우시안 분포, 마지막 데이터 분포 즉 시작과 끝은 바뀌지 않는 다는 것입니다.
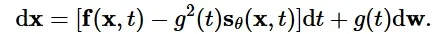
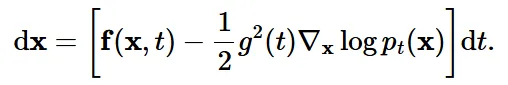
첫번째 수식이 SDE 수식이고, 두번째 수식이 probability flow ODE 수식입니다. 뒷 부분의 g(t)dw 즉 diffusion 부분이 제거됨으로서 deterministic 해진 것을 알 수 있습니다.
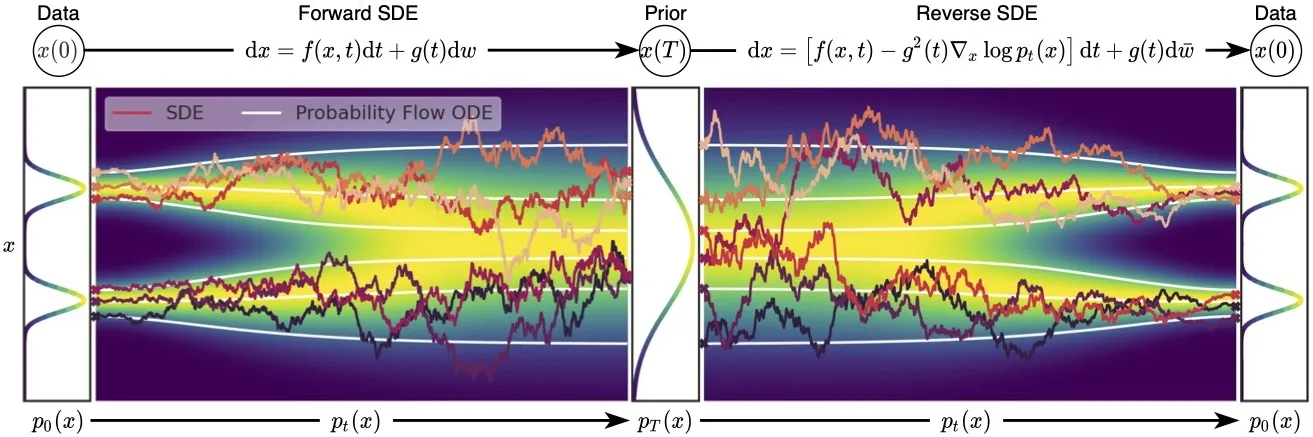
그림만 보아도 marginal distribution은 변하지 않고 경로만 바뀐 것을 알 수 잇습니다.
이렇게 SDE를 ODE로 바꾸면서 경로가 deterministic해져서 log-liklihood를 정확히 계산할 수 있을 뿐만아니라, probability flow ODE는 neural ODE와 continous normalizing flow의 특별한 경우가 되면서 2개의 속성을 상속받게 됩니다. 특히 change-of-variable의 속성을 상속받게 되어서 알 수 없는 데이터의 분포 에서 부터 로의 변환이 가능하게 됩니다.
Controllable generation for inverse problem solving
Score-based generative model은 inverse problem을 푸는데 적절합니다. 를 알고 있을 때 를 계산하는 것이 inverse problem입니다. 조금더 일반적으로 설명하자면 y를 알고 있을 때 x를 구하는 것입니다. 베이지안 정리를 통해서 로 나타낼 수 있습니다. 이후
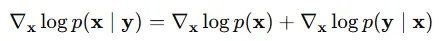
이전 식의 양변에 Score function을 취하면 위의 식을 얻습니다. 는 우리가 이미 알고 있고, p(x)는 score model의 학습을 통해서 쉽게 구할 수 있기 때문에 를 구하는 것 역시 쉬울 것입니다.



Score-base generative model을 inver problem에 적용한 예시들입니다.
Connection to diffusion models and others
Score matching 방식을 energy based model에 단순히 적용시켰을 경우 MNIST dataset으로도 결과가 나오지 않았습니다. 따라서 3가지 방식을 향상시켰다고 저자는 언급햇습니다.
- 다양한 스케일의 노이즈를 데이터에 추가하고 이를 기반으로 score function을 학습시켰습니다.
- U-Net(RefineNet)을 score-base model에 사용했습니다.
- Langevin MCMC Sampling을 각 노이즈 스케일마다 적용했습니다.(Corrector)
