Neural Ordinary Differential Equations 논문리뷰

이한결·2024년 12월 30일

참고 영상: https://www.youtube.com/watch?v=EhyrwwjVuWU

해당 강의가 시각적으로 Neural ODE를 정말 잘 설명해 주었다고 생각해서, 해당 강의를 먼저 듣고 더 깊게 공부하시고 싶은 분들은 아래 내용을 참고하시면 좋을거 같습니다.

Introduction

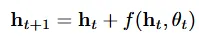
CNN을 공부하신 분이라면 위의식이 ResNet의 residual block을 뜻한다는 것을 한눈에 파악하실 수 있을겁니다. 기존의 normalizing flow는 위와 같이 residual network를 이용해서 반복적으로 업데이트 했습니다.

ResNet도 layer의 개수에 따라 18,50,101.. 이렇게 여러 종류가 있는데 개수가 많아질수록 일반적으로 성능이 더 좋아졌습니다. 그러면 어떻게 하면 layer의 개수를 늘리지만 더 적은 step을 사용할 수 있을까요? 그런 방법이 있기는 할까요?

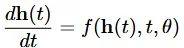
네 있습니다. 논문에서 해당 방법으로 ordinary differential equation (ODE)를 제시했습니다. 입력 layer h(0)에서 시작해서 출력 layer를 거쳐서 h(T)를 얻을 수 있습니다. 이는 black-box differential equation solver를 통해서 구할 수 있습니다.

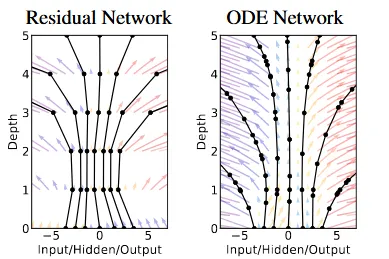
아래에서 더 자세한 설명이 있으니 지금은 ODE는 더 깊은 layer를 더 적은 step만으로 가능하게 했어! 라는 컨셉을 기반으로 이해하시면 됩니다. 위의 그림은 왼쪽이 Residual network 오른쪽이 ODE network입니다. 왼쪽그림은 먼가 단절되었지만, 오른쪽 그림은 먼가 이어진것처럼 느껴질 겁니다. 또한 화살표의 수가 오른쪽이 훨씬 더 많은 것을 알 수 있습니다. 이전에 말한 컨셉인 더 많은 step을 가능하게 할 수 있는 느낌이 어느정도 오실 것 입니다.

ODE Solver를 사용함으로서 다음과 같은 이점을 얻을 수 있습니다.

Memory efficiency: Back propagation을 진행할 때 값들을 저장하기 않고 진행함으로서 메모리 사용량이 일정하게 유지되어 깊고 복잡한 연속 모델을 효율적으로 학습할 수 있습니다.
Adaptive computation: Neural ODE는 Apaptive ODE Solver를 사용해서 복잡도에 따라 계산량을 자동으로 조정합니다.
Scalable and invertible normalizing flows: 생각지 못한 이점으로 change of variables 공식을 더 쉽게 계산할 수 있게 됐습니다.
Continuous time-series models: RNN에서는 동일한 시간간격의 데이터를 사용해야 하지만, ODE에서는 시간 간격이 동일하지 않아도 사용할 수 있습니다.

Reverse-mode automatic differentiation of ODE solutions

Continous-depth network를 학습시킬 때 가장 어려운 점은 reverse-mode의 ODE Solver를 통한differentiation 입니다. 쉽게 말해 Back propogation이 힘들다는 것입니다.

Adjoint sensitivity method는 메모리 비용이 낮아지고, 파라미터(시간 간격)에 따라 계산량과 오류를 증감 시킬 수 있고, 모든 ODE Solver에 적용할 수 있습니다.

Forward process

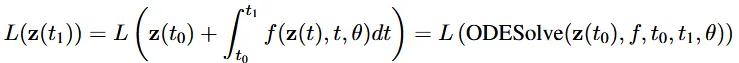
우선 forward 과정에서 사용되는 Loss function L()부터 알아보도록 하겠습니다. 수식은 복잡해보이지만 개념이 간단하니 쫄지 않고 천천히 따라오시면 이해하시기길 쉬우실겁니다.

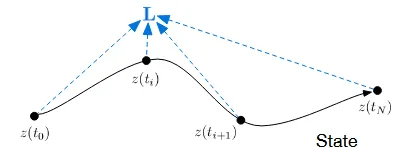
시작 지점은 맨 왼쪽의 $z(t_0)$ 입니다. 시작이 0이고 끝이 1이라고 생각하시면됩니다. 따라서 위의 L()수식을 보면 맨 왼쪽의 수식이 $L(z(t_1))$ 으로 나타나져있는데, 우리는 끝 지점 1을 예측하는 것이기 때문에 $t_1$ 에 대한 Loss를 구하는 것입니다.

왼쪽에서 오른쪽 방향으로 진행이되는 것을 시각적으로 확인할 수 있습니다. 0에서부터 1까지 가는데 중간에 $t_i$ 도 거치고 $t_{i+1}$ 도 거치고 하는 것을 알 수 있습니다. 그러면 0에서 i, i에서 i+1로 이동하는건 어떻게 하냐라는 궁금증이 생기실겁니다. 바로 기울기를 통해서추정하는 것입니다.

해당 과정은 Backward 과정이기때문에 일단 기울기를 통해서 어떻게 다음 step으로 가는지만 넘어가고 추후에 Backward 과정 자체는 다시 설명해드리도록 하겠습니다. 맨 오른쪽의 파란색 화살표에서 시작해서 주황색 곡선이라는 기울기를 따라서 다음 단계의 값을 구할 수 있습니다. 이처럼 Neural ODE의 핵심은 ODE 즉 미분 방정식을 구하는 것입니다.

다시 돌아와서 우리는 다음 단계를 가기 위해서 미분값을 이용했고, 이러한 과정을 반복하다보면 마지막 시점인 1에 도착할 것입니다. 제가 방금 설명한 이러한 과정을 반복한다가 Loss function의 가운데 적분 수식입니다. 0에서부터 1까지 이러한 과정을 반복하고, 시작지점이 0이기때문에 가운데 수식이 완성되는 것입니다.

Backward process

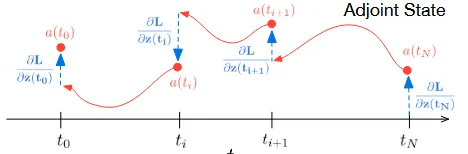
Backward도 Forward랑 동일하게 작동합니다. 원래 Backward를 진행하기 위해서는 미분값들을 다 저장해서 Backpropogation을 진행하지만, Neural ODE에서는 Forward에서 사용한 초기 시점과, 기울기를 더해주는 과정을 하기 때문에 메모리를 아낄 수 있다고 하는 것입니다.

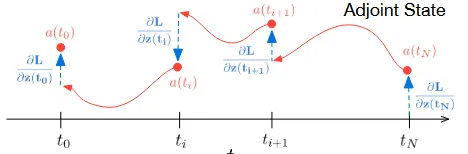
어떻게 동작하는지 대충을 알겠는데 그러면 그림 위에 나와있는 a는 머고, 이상한 분수식은 머냐 라는 의문이 생기실 것 입니다. 우선 a(t) = ∂L/∂z(t)는 adjoint state로서 시간 t에서 예측한 z(t)의 값이 Loss function에 미치는 영향력을 나타냅니다. 쉽게 말하면 해당시점(t)에서 얼마나 많이 틀렸냐를 나타내는 지표입니다.

Forward 과정에서는 값을 이용해서 최종시점을 예측했다면, Backward 과정에서는 얼마나 틀렸는지를 나타내는 adjoint state값을 이용해서 진행됩니다.

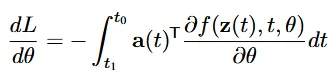
또한 Forward 과정에서는 f라는 함수의 gradient를 이용해서 이동했다면, Backward 과정에서는 a라는 함수의 gradient를 이용해서 이동합니다. 위의 수식이 Backward의 이동과정을 나타내는 수식입니다.

알고리즘이 위와 같이 나와있긴 하지만, 해당 내용은 너무 축소되었고, 더 자세한 내용들은 전부 Appendix를 참고하시면 될거 같습니다.

알고리즘을 요약하면 다음과 같습니다.

Forward process: 초기 값으로부터 gradient를 더해서 최종 값을 예측

Backward process: 예측의 오차를 나타내는 adjoint state로부터 gradient를 더해서 각 시점의 오차 예측

Replacing residual networks with ODEs for supervised learning

해당 부분에서는 neural ODE를 supervised learning 시키는 내용에 대해서 다루게 됩니다.

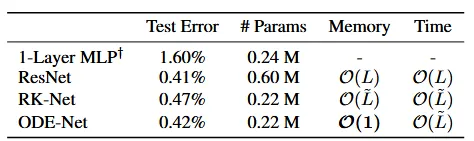
ResNet: 입력을 2번 downsampling을 진행하고, 6개의 Residual Block 사용

RK-Net: Forwar와 Backward 과정 모두 Runge-Kutta ODE Solver를 사용

ODE-Net: 논문에서 제시한 방법인 neural ODE 방식을 사용

[Test Error]

ResNet, ODE-Net, RK-Net, MLP 순으로 성능이 좋습니다. 성능 부분에서는 ResNet이 가장 뛰어난 것을 확인할 수 있습니다.

[#Params]

다음으로 파라미터의 개수입니다. ResNet이 압도적으로 많은 것을 확인할 수 있고, RK-Net과 ODE-Net이 MLP보다 파라미터의 개수가 작은 것을 확인할 수 있습니다.

[Memory]

Memory 측면에서 ResNet은 Layer의 개수(L)만큼 필요하고, RK-Net은 Solver 평가 횟수에 따라 시간 비용이 증가하고, ODE-Net은 Adjoint state 덕분에 Layer 수와f 무관하게 작동합니다.

[Time]

ResNet은 Layer의 개수만큼, RK-Net과 ODE-NEt은 ODE Solver의 평가 횟수에 따라 변하는 것을 확인할 수 있습니다.

결론적으로 ODE-Net은 적은 파라미터와 메모리로 ResNet과 유사한 성능을 달성했습니다.

Error Control in ODE-Nets

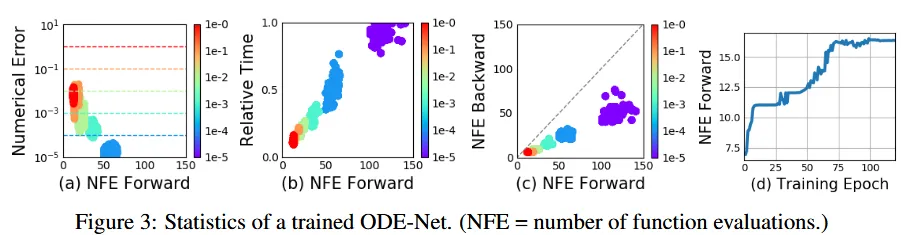
위의 그림을 보면 ODE-Net의 NFE의 증가에 따라 결과가 어떻게 변하는지 확인할 수 있습니다. 여기서 말하는 NFE는 number of unction evaluations의 약자로서 0부터 1까지 간다고 했을 때 NFE가 50이면 한번에 0.02 step만큼 나눠서 가게됩니다. 즉 NFE는 얼마나 조밀하게 갈것이냐를 나타냅니다.

(a) 그림을 보면 당연하겠지만, 조밀하게 영역을 나눌수록 성능이 더 좋아지고, (b)역시 조밀해질수록 시간이 더 오래 걸리는 것을 확인할 수 있습니다.

(c)부분에서 NFE가 커질수록 즉 조밀해질수록 파라미터dfadfadfzvdf 수가 많아지는 것은 당연한데, 추가적으로 점선이 Forward 과정에서의 파라미터 수를 나타내는데 항상 점선의 아래있는 것을 보아 Adjoint state를 사용함으로서 파라미터 수를 많이 줄인 것을 알 수 있습니다.

ResNet에서는 모델의 depth를 layer의 개수로 평가하는데, ODE-Net에서는 layer라는 명확한 개념이 없어서 NFE의 개수를 기준으로 depth를 정합니다. (d) 그림을 보면 학습이 진행될수록 NFE가 커지는 것을 알 수 있습니다.

Continous Normalizing Flows

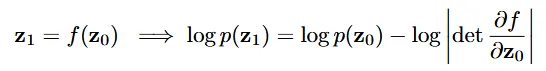
ResNet에서 사용하는 discretized equation은 Normalizing flows에서도 사용되는 방식입니다. 위의 Normalizing Flow 수식에서 $z_1$ 을 구할 때 $z_0$ 에서 determinant를 빼서 구하는 것을 확인할 수 있습니다. Normalizing flow에서 PDF를 변환하는 과정에서 Change of variable이 사용되는데, 위의 과정에서 determinant가 대부분의 계산 비용을 차지합니다.

Discrete한 layer들을 continous하게 바꾸면 determinant의 계산을 간단하게 할 수 있습니다.

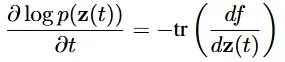
어떻게 간단하게 바꾸냐는 이전부터 많이 언급해서 대충 눈치는 채졌을 겁니다. 바로 determinant를 Trace(대각 행렬 곱)으로 변환하는 것입니다. 위의 수식은 해당 과정을 Theorem1에서 정리한 것입니다. z(t)는 continous random variable이고, 해당 값의 pdf에 로그 변화율을 trace로 구할 수 있습니다. 증명은 논문의 Appendix A를 참조하시면 됩니다.

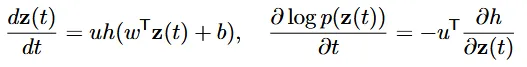
위의 determinant 대신 continous를 적용해서 Trace를 구하는 방식을 planer flow에 적용한 결과입니다. 이렇게 적용한 결과 계산 비용이 $O(M^3)$ 이 었던 원래 모델에서 linear하게 $O(M)$ 으로 변경할 수 있습니다.

[Continous Normalizing Flow]

시간 t에 따라 PDF가 변하도록 설계된 Continous Normalizing Flows(CNF)의 함수는 f(z(t),t)로 정의할 수 있습니다.

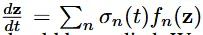
위의 수식에서 사용된 방식은 gating mechanism으로서 $\sigma$ 값인 0또는 1의 값을 가져서 f를 포함할지 안할지를 결정할 수 있습니다.

Density matching

CNF는 Adam을 사용한 10,000번의 iterations, NF는 RMSprop을 사용한 500,000번의 iterations를 적용했습니다. 이 Task는 원본 데이터의 분포와 KL Divergence를 최소화 하도록 학습됐습니다.

맨오른쪽 Loss그림에서 CNF가 NF에 비해 더 낮은 값을 기록한 것을 확인할 수 있습니다. NF의 K는 layer의 개수, CNF의 M은 hidden unit의 값을 나타냅니다. 2개 모두 커질수록 학습량이 많아지고 성능이 좋아지는 지표입니다. CNF가 NF에 비해서 같은 값을 가질 때 성능이 더 좋은 것을 확인할 수 있습니다.

Maximum Likelihood Training

이전에는 KL Divergence를 이용해서 학습했다면, 이번에는 Maximum Likelihood Estimation(MLE)를 이용해서 학습을 진행합니다. CNF가 Change of Variable을 계산하는데 훨씬 용이하기때문에 MLE를 구하는 과정도 수행하기 용이합니다. 해당 Task에서 CNF가 64개의 hidden unit을 사용했으며, NF는 1개의 hidden unit을 가진 64개의 layer로 구성되었습니다.

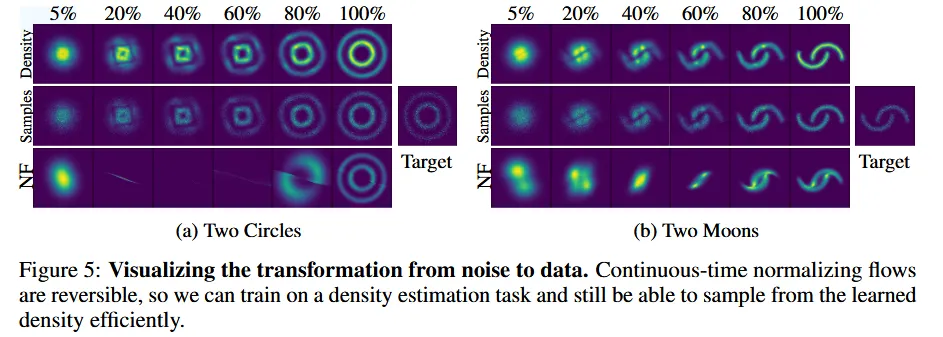
결과는 위와같습니다. 위의 2개의 행은 CNF를 마지막 행은 NF를 나타냅니다. CNF에서 Density로 전체적인 구조를 파악하고, Samples로 세부적인 부분을 파악할 수 있습니다.

CNF의 경우 데이터의 변화가 연속적이고 부드러운 것을 확인할 수 있고, NF의 경우에는 변환이 불규칙적이고 일정하지 않아 보입니다.

A generative latent function time-series model

주식과 같은 규칙적이지 않은 데이터를 neural network에 적용시키는 것은 어려운 방법입니다. 대부분 입력값으로 더미 형태나, 고정된 시간차이를 갖도록 변형됩니다. 이렇게 고정된 형태로 데이터를 변환하면 데이터의 손실이 발생할 가능성이 높습니다.

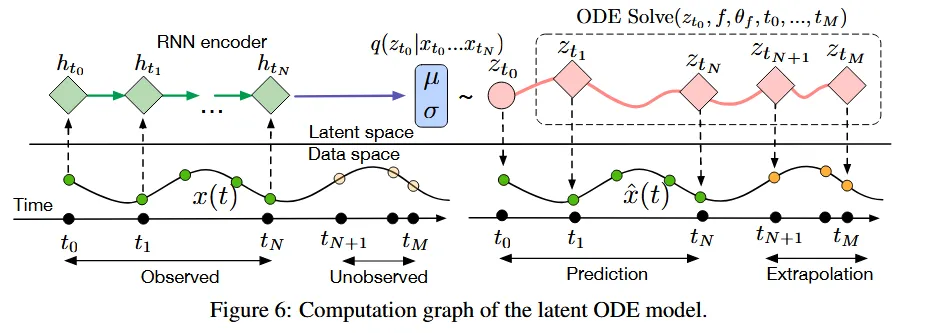
이러한 한계를 극복하기 위한 방식으로 continous한 neural ODE를 적용하면됩니다. 이전에 배웠던 방법처럼, ODE Solver는 $Z_{t_0}$ 에서 시작해서 gradient를 더해가면서 다음 state를 예측하게 됩니다.

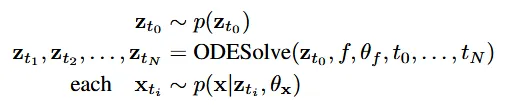
수식은 위와 같습니다. ODE Solve를 통해서 다음 단계를 예측하게 되고, 각 단계는 하나의 확률 분포를 나타내게 됩니다. Gradient를 이용해서 다음 단계를 예측할 수 있기 때문에 Unobserved된 값들까지 Extrapolation해서 알 수 있게됩니다. 또한 RNN은 동일한 시간 간격을 가져야하지만, ODE Solve는 동일한 시간간격일 필요는 없습니다.

정확하게 어떻게 동작하는지 알아보도록 하겠습니다. 우선 $Z_{t_0}$ 의 값을 얻기 위해서 time series의 역순의 데이터들을 RNN에 넣습니다. 따라서 RNN의 출력값이 ODE Solve의 입력값이 됩니다. 이후 ODE Solve를 통해서 Unobserved 데이터를 예측하게 됩니다. 예측된 값들은 latent space 상에 존재하기때문에 예측 된 값들 각각에 대해서 VAE를 통해서 원래의 데이터 형태로 복원되게 됩니다. 예를들어서 그림처럼 노란색 3개의 점을 예측했다면, 3개의 점 각각에 대해서 VAE를 적용합니다.

Poisson Process likelihoods

Poisson Process(포아송 과정)은 특정 시간 구간에서 사건이 발생하는 확률을 모델링하는 확률적 과정입니다.

Time-series Latent ODE Experiments

1000개의 2차원 나선형 데이터를 서로 다른 시작점으로부터 100 equally-spaced timesteps 진행한 결과를 RNN과 neural ODE를 비교합니다. 반은 시계방향 반은 반시계방향으로 돌도록 지정하고, gaussian noise를 추가해 결과물을 realistic하게 만들었습니다.

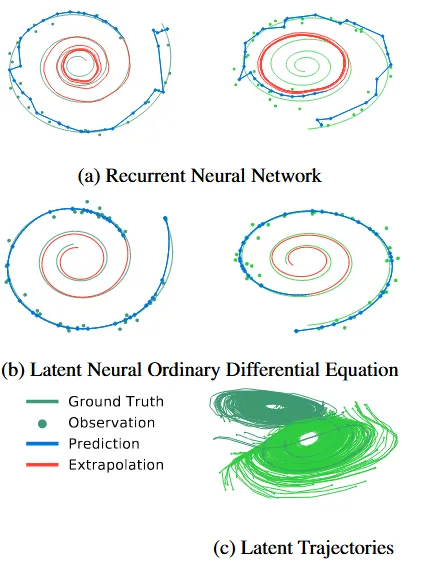
(a)는 RNN의, (b)는 Neural ODE의 Reconstruction&Extrapolation 결과입니다. 파란색 선이 모델의 예측, 빨간색 선이 Extrapolation의 결과입니다. 결과를 보시면 Neural ODE가 RNN에 비해서 예측이 실제값과 더 비슷하게 나타나고 추가적으로 Extrapolation 을 나타내는 빨간선도 ground truth와 더 비슷한 것을 알 수 있습니다.

Time series with irregular time points

이번에는 irregular한 timesteps의 경우에 대해서 결과가 어떻게 나오는지 알아보도록 하겠습니다. n=30,50,100일 때 RMSE(root-mean-squared eroor)의 값을 비교합니다.

결과를 보면 ODE가 RNN에 비해서 RMSE가 월등히 낮은 것을 확인할 수 있습니다. 더 많은 비교들은 Appendix F를 참고하시면 됩니다.

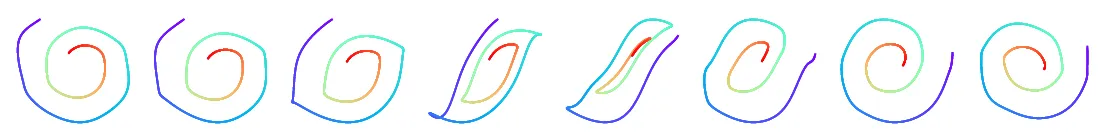
추가적으로 시작점의 위치 $z(t_0)$ 만 바꿔줬을 때 반시계 방향 → 시계 방향으로 방향변환이 smooth하게 잘되는 것을 확인할 수 있습니다.

Scope and Limitations

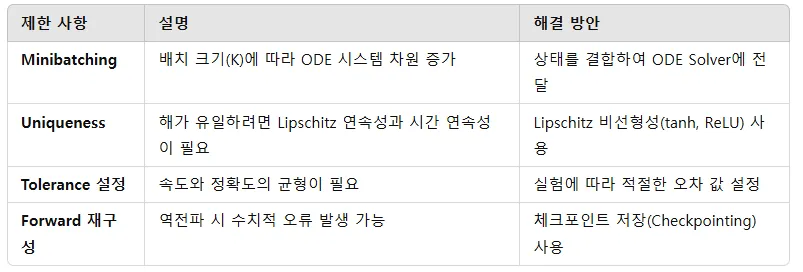
4가지(미니배치, Uniqueness, Tolerance, Forward 오류) 경우에 발생하는 문제와 이에 대해서 해결 방안을 간단하게 표로 정리한 것입니다.

Minibatching: 미니배치는 상태를 결합해 처리할 수 있지만, 일부 계산 비용이 추가될 수 있습니다.
Uniqueness: Lipschitz 연속성과 시간 연속성을 만족하면 ODE의 해는 유일합니다.
Tolerance 설정: 정확도와 계산 속도의 균형을 위해 상황에 따라 적절한 허용 오차를 설정해야 합니다.
Forward Trajectory 재구성: 역전파 과정에서 수치적 오류가 발생할 수 있으나, 체크포인트 저장을 통해 해결할 수 있습니다.