Introduction

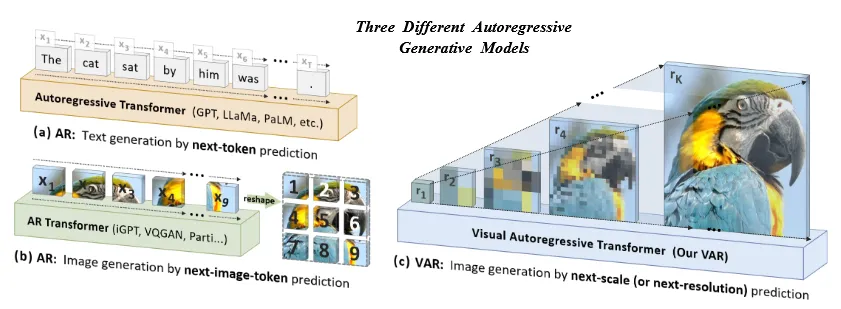
AutoRegressive(AR)모델의 성공은 크게 2가지 분야에서 눈에 띄게 나타났습니다. 첫번째로 GPT 시리즈와 LLM입니다(그림 a). 다음 토큰을 예측하면서 진행되는 방식으로 Self-supervised learning, Scaling Laws(작은 모델의 성능을 바탕으로 큰 모델 예측), Zero-shot & Few-shot 방법이 사용됐습니다. 두번째로 이미지 생성 분야 입니다(그림 b). 연속된 픽셀 값을 2D Grid로 변환한 후, 이를 Flatten해서 1D 시퀀스로 바꾼후 순서대로 다음 픽셀을 예측하는 방식으로 진행됩니다. 대표적으로 VQGAN과 DALL-E 모델이 있습니다.

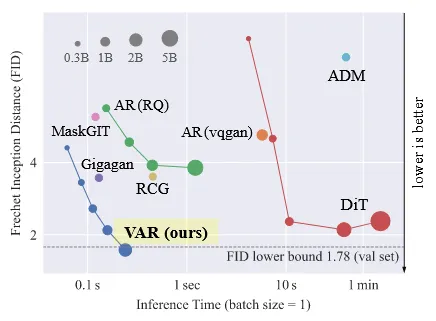
AR 모델이 비전에 사용될 때 스케일링 법칙이 사용되었지만, 아직 많은 연구가 나오지 않았고 Diffusion 모델에 비해서 성능이 많이 떨어집니다. 위의 사진은 초록색 AR모델들이 오른쪽 DiT(Diffusion) 모델에 비해서 FID가 높은 것을 확인할 수 있습니다.

해당 논문에서는 AR 기반 모델을 만들기 위해서 다시 한번 “order”라는 개념을 고려했습니다. 인간이 이미지를 인지할 때 큰 그림을 보고 이후 디테일한 부분을 보는 “order”가 정해져있습니다. 이러한 multi-scale, coarse-to-fine 전략을 기반으로 해당 논문에서는 next-scale prediction(그림 c) 모델을 제시했습니다. 기존 모델에서 다음 픽셀을 예측하도록 설계되었다면, 해당 논문에서는 다음 scale을 예측하도록 설계했습니다. 다음 스케일을 예측하도록 설계된 모델의 이름은 Visual AutoRegressive (VAR) 모델이라고 불려지고, 위의 그림에서 보이는 것처럼 Diffusion 모델의 FID 성능을 능가하는 결과를 초래했습니다. VAR은 GPT-2 기반 transformer 아키텍처를 사용합니다.

논문이 기여한 점은 다음과 같습니다.

1. Computer Vision 분야에서 next-scal prediction이라는 새로운 multi-scale autoregressive 프레임 워크를 생성했다.
2. LLM의 Scaling Lasw와 zero-shot generalization 기법을 처음으로 모방했다.
3. 처음으로 diffusion 기반 모델의 성능을 뛰어넘었다.
4. VQ tokenizer와 autoregressive model 훈련 파이프라인을 포함한 과정을 open-source code suite를 제공합니다.

Related Work

Properties of large autoregressive language models

Scaling laws

Scaling Laws는 모델 크기, 데이터 양, 계산량과 성능 간의 거듭제곱 관계를 규명하여, 작은 모델로부터 더 큰 모델의 성능을 예측하고 자원을 효율적으로 최적화할 수 있게 돕는 법칙입니다. LLM은 해당 방식을 이용해서 엄청난 크기를 증가시켰고, 이에 따라 엄청난 성능 개선이 있었습니다.

zero-shot generalization

Zero-shot generalization은 모델이 한 번도 명시적으로 학습하지 않은 새로운 작업이나 데이터에 대해 수행 능력을 보이는 것을 의미합니다. CLIP, SAM, Dinov2처럼 다양한 모델들이 zero-shot 기법을 기반으로 나타납니다.

Visual generation

Raster-scan autoregressive models

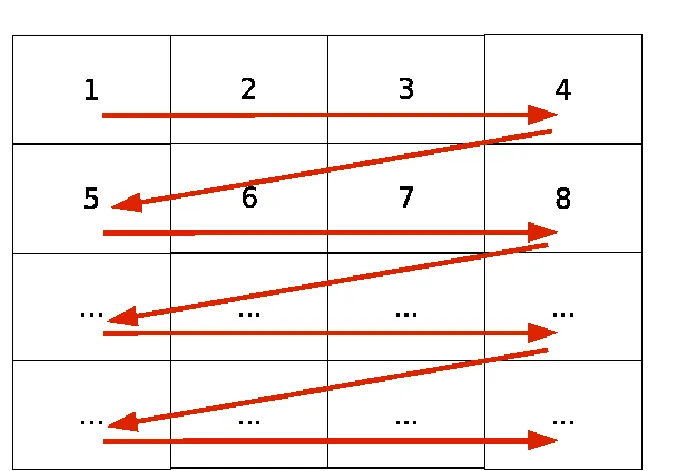
Raster-Scan 방식은 이미지를 왼쪽에서 오른쪽으로, 위에서 아래로 예측하는 방식입니다. 2D 이미지의 경우 1D 시퀀스로 변환한 후 다음 픽셀을 예측하는 형태로 진행합니다.

Masked-prediction model

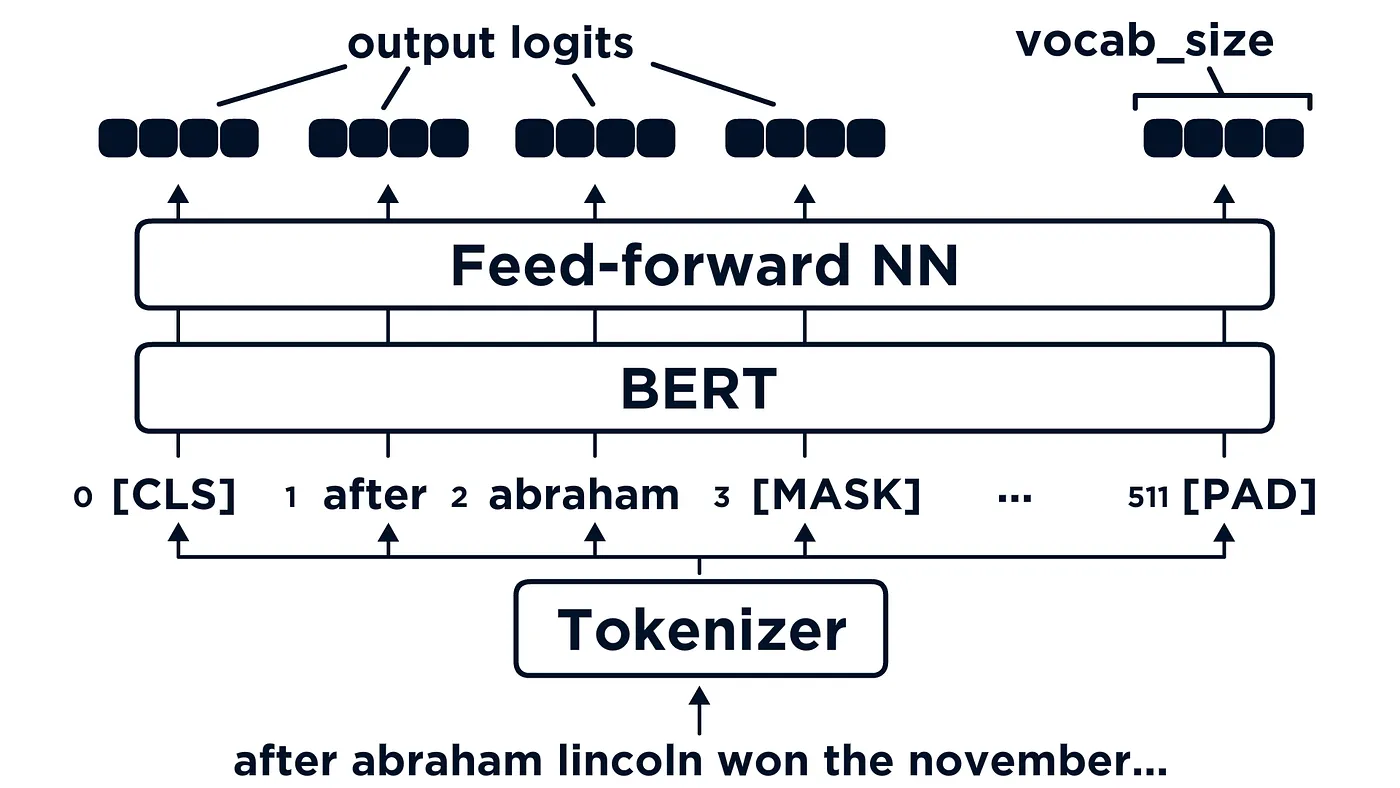
BERT에서 사용한 마스크 예측 기법을 기반으로 VQ autoencoder를 실행시키는 방법입니다. 마스크 예측 기법은 여러개의 토큰이 있을 때 이중에서 랜덤한 토큰을 N개 설정하여, 해당 토큰의 값을 MASK(NULL) 값으로 변경한 후, 해당 MASK를 예측하는 형식으로 진행됩니다.

Diffusion models

Diffusion model은 sampling, guidance, latent leraning 혹은 DiT, U-Vit처럼 U-Net을 transformer로의 변형을 하는 것처럼 많은 방법으로 발전되었습니다.

Method

Preliminary: autoregressive modeling via next-token prediction

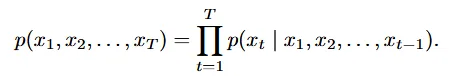
t시점의 토큰은 이전 시점 토큰들을 기반으로 생성됩니다. 이러한 unidirectional token dependency assumption은 위와 같이 나타낼 수 있습니다. 이전 토큰들을 기반으로 다음 토큰을 예측하는 next-token prediction의 수식은 쉽게 이해가 되실겁니다.

2D 이미지에 위의 수식을 바로 진행시키려면 1D로 변환시켜야합니다. 즉 첫번째로 이미지를 tokenize해서 discrete한 토큰들을 생성하게 한 후, 두번째로 토큰들을 1D 차원으로 나타내야합니다.

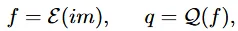
$\epsilon$은 Encoder를 나타내고, im은 원본 이미지를 나타내고, 2는 quantizer를 나타냅니다. 앞의 2개는 어느정도아실텐데 quantizer를 조금더 자세히 설명해드리자면 feature vector(f)를 학습가능한 codebook으로 매핑해주는 것입니다.

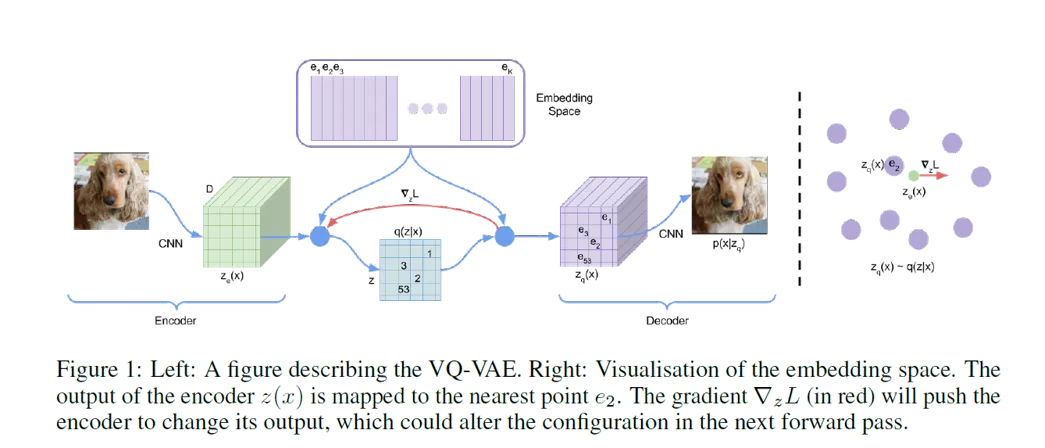
위의 사진은 VQ-VAE 논문에서 가져온 사진인데, 이미지 CNN을 통해서 feature map을 생성하고, 이를 기반으로 codebook을 생성하고, codebook을 Decoder에 넣어서 다시 이미지를 생성하는 과정입니다. 제 설명이 부족해서 https://www.youtube.com/watch?v=wA5MhRo2ApQ 해당 링크의 영상을 참조하면 더 쉽게 이해가 되실겁니다.

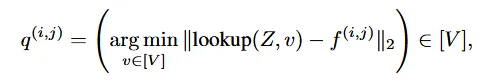
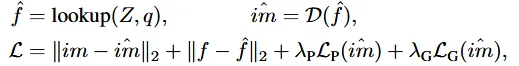
어쨌든 codebook을 생성할 때는 Euclidean 거리가 가장 작은 벡터를 선택하고, 이후의 과정은 위에서 설명한 것처럼, code book을 기반으로 보라색 feature map $\hat{f}$를 생성하고 이를 Decoder에 넣어서 이미지를 생성하는 것입니다.

Autoregressive model의 단점

1. Mathematical premise violation

Encoder를 통해서 feature map을 생성할 때 커넝을 사용하기 때문에 Autoregressive에서 사용하는 원리인 t시점의 픽셀은 이전시점에 의해서만 영향을 받는다는 점을 위반하게 됩니다.

1. Inability to perform some zero-shot generalization

단방향성으로 모델이 진행될 경우 zero-shot으로 생성하기 어렵습니다.

1. Structural degradation

2D 배열을 1D로 변환하면서 구조적 손상이 발생하게 됩니다. 2D 상에서는 인접한 영역들이 1D로 변환되면서 멀리 떨어지게 되기 때문에 이러한 문제가 발생합니다.

1. Inefficiency

Computational cost 측면에서 self-attention tansformer는 $O(n^2)$이지만 autoregressive step은 $O(n^6)$으로 계산 비용이 많이 듭니다.

Visual autoregressive modeling via next-scal prediction

논문의 순서인 Stage2 → Stage1로 설명해드리겠습니다. Stage2를 볼 때 어떻게 multi-scale token이 생성되었는지 궁금하시더라도 조금만 참으면 아래에 설명이 나올 것입니다.

Reformulation(Stage2)

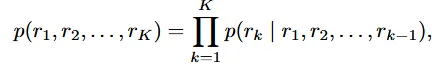
VQVAE의 방법을 사용하지만 next-token prediction 방법 대신 next-scale prediction 방법을 사용합니다. Encoder를 통해서 K개의 multi-scale toke maps을 얻습니다. 이때 여러개의 scale 변환은 interpolation 방법을 이용합니다. 마지막 K번째 token map의 resolution은 h X w이고 이전 token map은 이것보다 작은 resolution을 갖고 있습니다.

위의 그림은 방금 설명한 next-scale prediction 방법입니다. [S] Start Token을 이용해서 $\hat{r_1}$을 예측하고 ground truth인 r1과 Cross Entopy를 이용해서 차이를 계산합니다. 두번째로 [S]와 $r_1$을 interpolation을 통해서 차원을 $r_2$와 맞춰주고, transformer가 이해할 수 있는 형태로 바꾸기 위해서 word embedding을 취해준 값을 이용해서 $\hat{r_2}$를 구하고 마찬가지로 ground truth $r_2$와 Cross-Entropy를 통해서 차이를 예측합니다. 이러한 과정을 k번째까지 parallel하게 진행됩니다. 오른쪽에 나와있는 Block-wise causal mask는 이전단계의 정보들은 사용할 수 있고, 이후 단계는 사용할 수 없음을 시각화 한것입니다. 검은색 마스크는 이후이기때문에 사용할 수 없고, 회색 마스크는 사용할 수 있는 것입니다.

알고리즘은 위와 같습니다. 사실 해당 알고리즘은 알고리즘 1을 보고 와야 queue_pop 부분의 이해가 쉬울 것입니다. tokenization 설명 이후 알고리즘을 한번에 설명해드리도록 하겠습니다.

어쨌든 VAR는 기존의 VQVAE의 구조를 바꿈으로써 3가지 이슈를 해결했습니다.

1. Mathematical premise violation 해결

이전에 인코딩 과정에서 이후 픽셀의 정보를 미리 사용하는 bidirectional correlation 문제가 있었는데, 여기서는 픽셀이 아닌 scale 값이기때문에 무조건 이전 scale만 사용하는 unidirectional 관계가 됩니다.

1. Structural degradation 해결

VAR에서는 flatten 과정이 진행되지 않고, 생성된 multi-scale token들은 각각의 픽셀들은 연관더어 있기 때문에 구조적 손상이 발생하지 않습니다.

1. Inefficiency 해결

n X n latent는 계산 비용을 $O(n^4)$으로 감소시켰습니다. 자세한 내용은 Appendix를 참조하시면 됩니다.

Tokenization(Stage1)

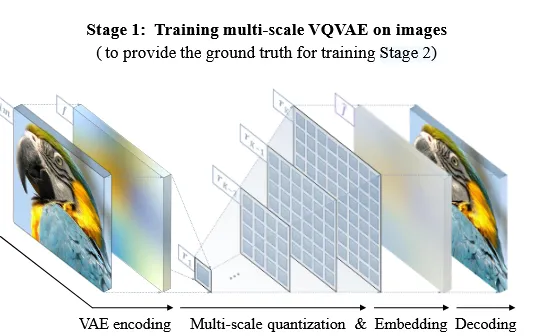
Stage2에서 인코딩을 통해 생성된 feature map을 mult-scale token으로 변환되는 과정이 생략됐는데 그 과정을 설명해드리도록 하겠습니다. VQGAN과 똑같은 아키텍처를 사용했지만 quantiztion layer는 수정했습니다.

위의 알고리즘을 살펴보기전에 공통된 codebook Z를 사용한다는 의미를 설명해드리도록 하겠습니다. 물론 한번에 이해되시는 분들도 있겟지만, 저는 이해력이 부족해서 서로다른 차원을 갖는 multi-scale token을 어떻게 같은 차원의 codebook Z를 사용하지 라는 의문이 생겼었습니다. 하지만 잘 생각해보면 codebook으로 매핑하는 정보는 token전체가아니라 token에서 픽셀 하나입니다. 예를들어서 4x4xC의 resolution을 갖고있는 토큰은 16개의 픽셀값이 codebook의 길이에 해당하는 V중 하나에 매핑 될 것입니다.

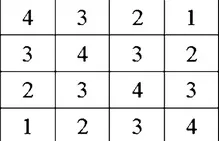
V가 4라면 1~4사이의 값을 생성하도록 위의 결과가 나올 것입니다.

이제 Codebook Z를 공유한다는 개념을 명확히 이해했으니, 알고리즘 1을 살펴보도록 하겠습니다. 입력값으로 원본 이미지(im)가 들어가고, multi-scale을 결정하는 하이퍼파라미터 K를 정합니다.인코더($\epsilon$)을 통해서 feature map(f)을 생성하면 for문을 들어가기 전 준비과정이 완료된 것입니다.

이후 for문에서는 feature map(f)를 k번째 해당하는 resolution으로 interpolate하고, 해당 값을 R이라는 큐에 입력합니다(이후 알고리즘2에서 사용하기 위해). 그다음 interpolation된 $r_k$는 codebook에서 비슷한 벡터를 찾는 lookup과정을 진행해서 $z_k$로 변합니다(위의 예시에서 1~4에 해당하는 값 찾는 과정). $z_k$는 실제로 벡터이기 때문에 k번째 토큰의 차원과 동일하게 변환시켜주기 위해 interpolate를 취해주고, 해당 값을 f에서 빼줍니다. 이전에 봤던 알고리즘 2에서는 더해줬는데 왜 여기서는 빼줄까요? 바로 인코더 디코더 과정의 차이라고 보시면됩니다. 우리가 PCA알고리즘을 적용할 때 가장 중요한 요인을 찾고, 그 값을 빼고 그다음 중요한 요인을 찾는 과정을 했던 것처럼, 첫번째로 사람이미지에서 얼굴에 대해서 학습했을 경우 그 feature를 빼고 눈, 코, 입 이런 요소들을 학습할 수 있도록 해주는 것입니다. 즉, 점점 더 디테일한 요소를 학습하도록 f값에서 빼주게 되는 것입니다.

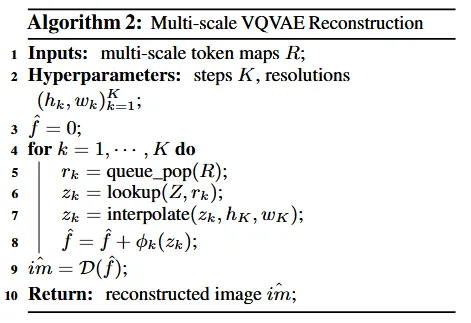
알고리즘1을 봤으니 다시 알고리즘2를 보면 쉽게 이해가 되실겁니다. 알고리즘1에서 생성한 multi-scale token maps(R)이 입력값으로 들어오게 됩니다. 초기 $\hat{f}$는 0으로 설정하고 이후 해당값은 이전 scale에서 예측한 feature가 됩니다. for문에서는 queue의 맨아래에 있는 요소를 가져와서 code book 벡터로 변환한 후 이를 k번째 resolution으로 interpolate 한후 $\hat{f}$값에 더해줍니다. 알고리즘1에서는 feature를 학습하기 위해서 빼줬다면, 여기서는 이미지를 생성하기 위해서 얼굴, 코, 눈, 입 이렇게 학습한 요소들을 더해주는 것입니다. for문 즉 mulit-scale 과정이 다 끝나면 Decoder(D)를 통해서 생성 이미지($\hat{im}$)이 나오게 됩니다.

Implementation details

Codebook의 길이 V=4096으로 설정했습니다. VQ-GAN 모델을 이용해서 multi-scale token map을 생성하고, standard decoder-only transformers GPT-2를 사용했습니다. Start token은 class embedding 값으로 넣고 adaptive noramlization(AdaLN)을 적용했습니다. 다른 추가적인 차원이나 파라미터들은 논문을 참조하시면 됩니다.

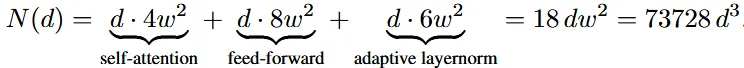
실험 설명을 용이하게 하기위해서 d값만 설명해드리자면 w=64d, h=d, dr(dropout late)= 0.1 X d/24 인 것처럼 d는 resolution과 파라미터의 수를 결정하는 요소입니다.

Empirical Results

State-of-the-art image generation

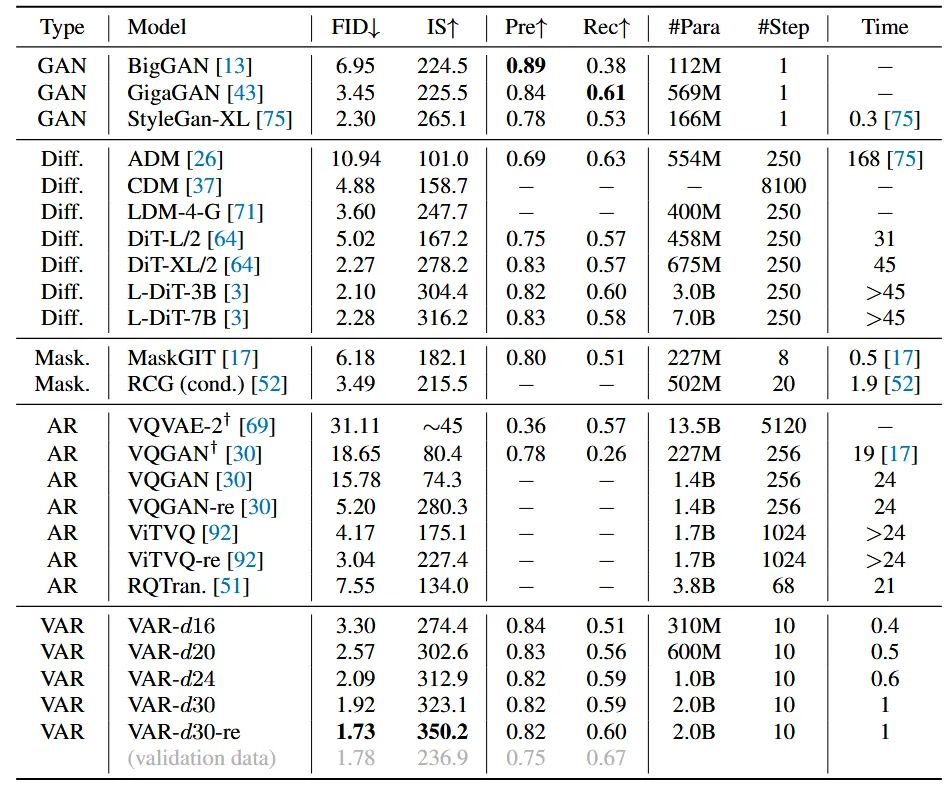
Type은 크게 GAN, Diff, Mask(BERT-style masked-prediction models), AR(GPT-style autoregressive models), VAR(visual autoregressive)로 나누어집니다. 우선 결과만 비교한다면 처음으로 diffusion성능을 뛰어넘은 autoregressive model입니다. 또한 diffusion 모델과 비교했을 때 파라미터 수나, 시간 적으로도 많이 개선된 것을 알 수 있습니다.

Power-law scaling laws

(해당 부분은 완벽하게 이해를 하지 못해서 더 자세한 내용은 논문을 참고하길 바라겠습니다.)

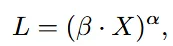
위의 수식에서 X는 파라미터 개수(N), 학습하는 토큰 수(T), optimal training comput($C_{min}$) 값의 영향을 받는 변수이고, L은 Normalized test loss, a는 거듭제곱 지수, B는 비례상수 입니다. 가장 중요하게 볼 요소는 loss값과 X 값입니다.

양변에 로그를 취하게 된다면 log(L)는 log(X)의 값이 선형적으로 영향을 준다는 것을 알 수 잇습니다. 해당 식을 통해서 결론적으로 모델 크기나 데이터 양 같은 변수를 늘림으로써 성능이 얼마나 증가할 수 있을지 예상할 수 있습니다.

VAR에서는 위의 scaling laws를 기반으로 12개 model을 설정했습니다. 파라미터는 18M~2B개 입니다.이미지 데이터는 최대 305B개 입니다. 모델이 최적의 학습 계산량($C_{min}$)에 도달했을 때 성능이 어떻게 개선되었는지 분석합니다.

이전에 설명한 것 처럼 파라미터의 수는 d의 값에 따라 결정됩니다($N(d) = 73728d^3$). d의 값을 6부터 30까지 12개의 종류로 설정해서 파라미터의 수를 18.5M ~ 2.0B가 되도록 설정했습니다. Loss값은 last scale(마지막 next-scale autoregressive step)과 global average 2가지 값을 비교했습니다. 결과는 위와 같습니다.

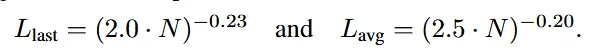
파라미터 수가 증가할수록 손실은 거듭제곱 법칙에 따라 감소합니다.

loss뿐만아니라 추가로 token error rate($Err$)도 측정했습니다. 이전과 비슷하게 선형적으로 감소하는 것을 알 수 있습니다.

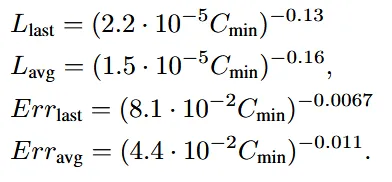
Optimal training comput($C_{min}$)이 증가할 때 Loss와 token error rate가 어떻게 감소하는지도 확인해봤습니다. 학습 계산량은 PFlops (PetaFLOPS) 단위로 측정

지수 값을 보면 avg가 last보다 더 작은 것을 확인할 수 있습니다. 기존에는 last가 avg보다 작았는데 서로 다르게 동작하는 것을 알 수 있습니다. 따라서 파라미터 수(N)는 마지막 스케일의 성능 개선에 더 효과적이며, 학습 계산량($C_{min}$)은 전체 스케일(평균 성능)의 개선에 더 효과적입니다. 이는 VAR Transformer가 파라미터와 계산량에 서로 다른 방식으로 반응한다는 것을 의미합니다.

요약하자면 LLM분야에서 확인된 Scaling Laws가 VAR 모델에서도 동일하게 작동한다는 것을 확인햇습니다. 따라서 큰 모델을 직접 학습시키지 않아도 작은 모델로 큰 모델의 성능을 예측할 수 있었습니다. 또한 파라미터를 늘리는게 좋을지 계산량을 늘리는게 좋을지 학습을 하지 않은 상태에서도 예측할 수 있게 된 것입니다. 파라미터 수를 늘리면 마지막 스케일 성능을 향상시킬 수 있고, 계산량을 늘리면 전체 평균 성능을 크게 늘릴 수 있습니다.

Appendix A에 있는 scali 갑스이 변화에 따른 이미지의 성능차이를 비교해 놓은 그림입니다. 확실히 계산량과 파라미터가 많은 오른쪽 아래의 그림이 가장 좋은 것을 확인할 수 있습니다.

Ablation Study

1,2의 비교를 통해서 VAR의 성능을 확실히 입증할 수 있습니다. FID가 가장크게(18.65 → 5.22) 감소한 것을 확인할 수 있습니다. 이후 AdaLN(Adaptive Layer Normalization), top-k sampling(확률이 높은 k개의 토큰만 고려), Classifier-free guidance(CFG), attention 과정에서 key와 query의 normalization을 통해서 성능이 향상되는 부분을 확인할 수 있습니다.

마지막 파라미터 수를 늘리는 Scale up 과정을 통해서 가장 많이 성능이 개선되는 것을 확인할 수 있습니다.

Limitations and Future Work

VQVAE Tokenizer 개선

기존 VQVAE 모델을 그대로 사용했지만 최근에 Tokenizer 연구를 통해서 더 좋은 방법의 양자화 기법들이 나왔습니다. 이를 VAR에 적용했을 때 더 좋은 성과를 얻을 수 있을 것입니다.

Text-prompt Generation

VAR은 기본적으로 LLM 모델과 비슷하므로, LLM과 통합한다면 텍스트-이미지 생성 모델로 쉽게 확장할 수 있을 것입니다.

Video generation

3D Next-Scale Prediction을 시간적 스케일을 고려해서 진행한다면 기존 AR기반 모델들보다 계산 복잡도를 줄인 상태로 모델을 개발할 수 잇을 것입니다. 따라서 더 긴 시간의 영상을 만들 수 있을 것입니다.

Code 결과

demo_sample.ipynb의 결과는 위와 같습니다. CFG를 이용해서 해당 class에 맞는 이미지는 잘 생성하는 것을 볼 수 있습니다.

demo_zero_sho_edit.ipynb의 결과는 위와 같습니다. 임의의 마스크를 생성해서 inpainting을 하는 과정인데…. 성능이 그렇게 좋지 않은 것을 볼 수 있습니다.