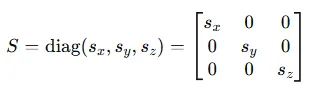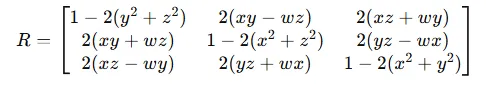출처: https://www.youtube.com/watch?v=XgE7tOSc7AU&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=12
한정현님의 컴퓨터그래픽스 11장 강의를 기반으로 제작한 블로그입니다.
Euler Transforms
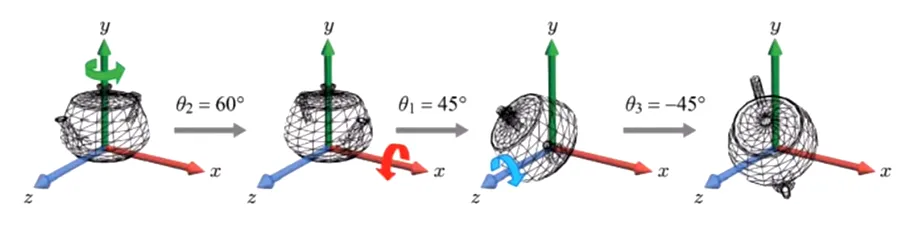
기존에 배운 물체에 대한 회전은 하나의 축에 대해서 진행했지만, 여러 축(x,y,z)를 기준으로 돌렸을 때 점이 하나의 평면(xy,yz,zx)에서만 회전하는게 아니라 3D 전체적으로 회전할 수 있습니다. 이렇게 모든 축을 기준으로 회전하는 변환을 Euler Transforms라고 합니다.
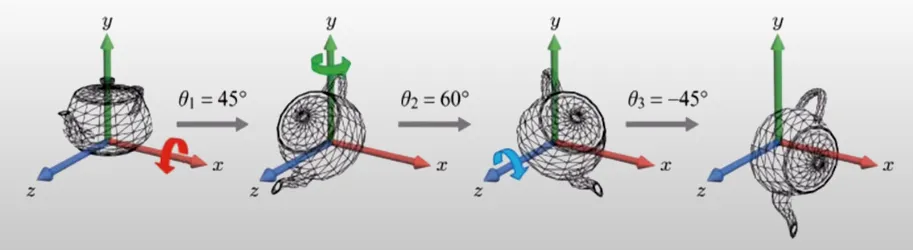
회전 순서를 바꾸면 어떻게 될까요? x,y,z축으로 회전하는 것을 y,x,z축으로 회전했을때 위의 사진과 같이 다른 결과가 나타나는 것을 확인할 수 있습니다. 즉 순서에 따라 결과가 달라집니다.
Keyframe Animation in 2D
Euler transfroms가 적용되는 keyframe에 대해서 설명해드리겠습니다. 애니메이션을 그릴 때 모든 frame의 이미지를 그리는 것은 시간적으로 육체적으로 힘든 방법입니다. 따라서 중요한 장면 예를들어서 1,13,24 frame을 책임자가 그리고, 그 사이의 2~12, 14~23 frame을 보조자가 그리는 방식으로 진행했습니다. 이렇게 책임자가 그리는 중요한 frame을 keyframes, 보조자가 그리는 frame을 in-between frames라고 합니다.
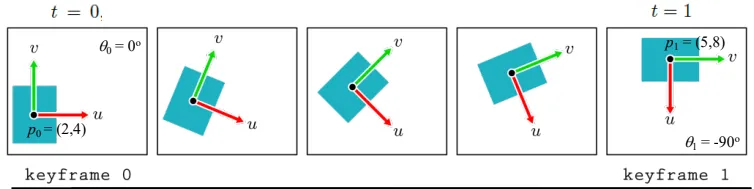
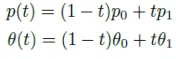
보조자가 생성하는 in-between frames를 keyframe의 interpolation을 통해서 컴퓨터로 구할 수 있습니다. 위의 수식이 간단한 interpolation 수식을 나타냅니다(p: 위치, : 각도).
Keyframe Animation in 3D
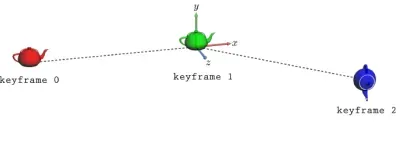
3차원에서 Keyframe의 변환을 생각해보겠습니다. Keyframe0에서 1까지 변환될때 단순히 x좌표만 변했고, 1에서 2로 변환될 때는 x축으로 90도, z축으로 -90도 변환된 것을 확인할 수 있습니다.
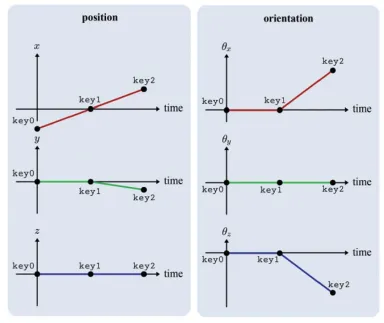
각 프레임별로 이동과 회전을 각각 생각해보면, 우선 0에서 1로갈 때는 x만 변하고 y와 z는 변하지 않습니다. 다음으로 회전할 때 xy평면에서만 위치 변화가 나타나기 때문에 x가 양의 방향으로, y가 음의 방향으로 변합니다.
회전의 경우 0에서 1로의 변환은 없고, 1에서 2로 변환될 때 x방향 90, z방향 -90이 변한 것을 확인할 수 있습니다.

이렇게 이동과 회전으로 나눈다음에 각 좌표(x,y,z)에 대해서 선형 보간을 통해서 특정 시점에서의 위치를 쉽게 얻을 수 있습니다. 그 결과 위와 같이 나올 것 입니다.
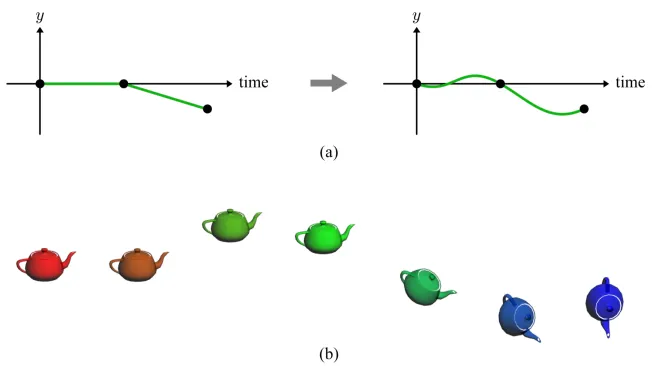
더 부드러운 변환이나, 중간에 어떠한 변화를 주고 싶을 때 고차원 함수나 함수를 변환할 수 있는 기능도 제공됩니다.
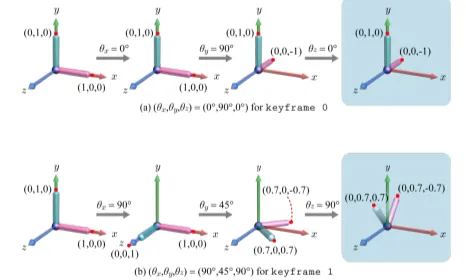
예시를 보면서 개념을 interpolation 과정을 확인해보도록 하겠습니다. 위와 같이 3개의 축으로 변환이 있는 frame0과 frame1의 결과가 있습니다. 이때 frame1/2를 구하려면 단순히 2개의 각을 합쳐서 2로 나눠주면 됩니다.
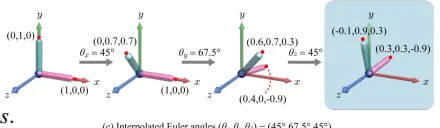
결과는 위와 같이 나오겠죠? 파란색 부분만 보면 반 정도 회전하겠구나 라는 느낌을 쉽게 받을 수 있습니다. 근데 지금 처음과 끝 모두 yz평면에 있어서 x값이 0인데 보간된 맨마지막 결과를 확인해보시면 -0.1과 0.3으로 yz평면에 있지 않습니다.
그래서 결론은 Euler transform이 직관적이긴 하지만 못 쓰겠다!
Quaternion
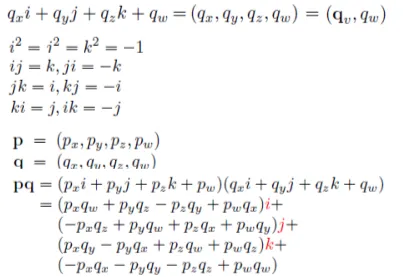
Euler transform대신에 in-between frame을 만들기 위해서 새로운 방식인 Quaternion을 소개해 드리겠습니다. Quaternion은 3개의 허수부와 1개의 실수로 이루어진 4개의 벡터 입니다. 기존에 i로 복소수를 표현했는데 j와 k 2개가 추가되고 각 성질은 위에 나와있습니다. 교환법칙이 성립이 안되는 등 중요한 규칙들이 있습니다.
2개의 quaternion p,q를 곱했을 때 마지막 결과 pq를 보시면 새로운 quaternion이 생성되는 것을 확인할 수 있습니다.
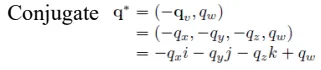
복소수 하면 생각나는 짝궁이 켤레 복소수인 것 처럼 quaternion의 복소수에 음수를 붙인 값을 Conjugate라고 합니다. 두 quaternion을 곱해서 나온 새로운 quaternion에 conjugate를 취하면 이 나오게 됩니다(순서 주의!)
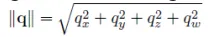
Quaternion의 크기는 각 계수를 곱해서 루트를 취해서 구할 수 있는데, 이때 크기가 1이라면 unit quaternion이라고 표현합니다.
2D Rotation ↔ Quaternion
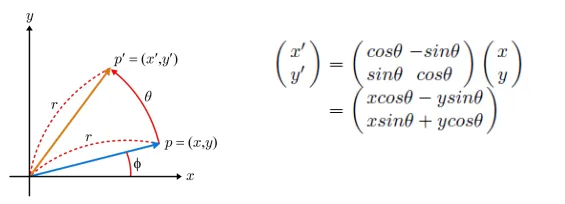
3장? 4장? 쯤에 봤었던 회전 변환 그림입니다. 를 이용해서 새로운 좌표를 구할 수 있었습니다.
이를 복소수를 이용해서도 표현이 가능합니다. 초기의 좌표를 라고 나타내고, 회전하는 변환을 로 나타내면 의 결과가 나타납니다. 이때 실수부가 x좌표, 허수부가 y좌표와 같다는 놀라운 점을 발견할 수 있습니다.
3D Rotation ↔ Quaternion
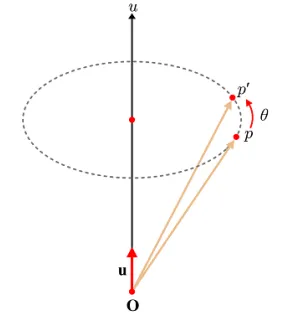
3차원의 회전도 quaternion으로 표현이 가능합니다. 초기 좌표 이라고 할 때 x,y,z좌표가 p가 돼서 허수부를 나타내고, 실수부는 0으로 나타냅니다. 이후 변환에 대해서 로 나타냅니다. 마찬가지로 앞부분이 허수부 뒷부분이 실수부 입니다.
이때 갑자기 u가 나왔는데 u는 q 변환을 unit quaternion으로 나타내기 위한 수단으로 회전하는 u축의 길이입니다. 부연설명은 해드리자면 q의 크기는 의 루트인데 u가 단위 벡터라서 q의 크기도 1이됩니다. 개인적으로 u를 안곱해도 q의 크기가 1이되는데 왜 곱한지에 대해서는 이해가 되질 않았습니다.
어쨌든 최종적으로 새로운 점 로 나타낼 수 있습니다.
in-between frame using quaternion
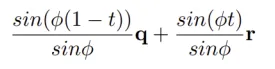
결론적으로 사이사이 frame의 interpolation은 위의 식을 통해서 정확하게 구할 수 있습니다.
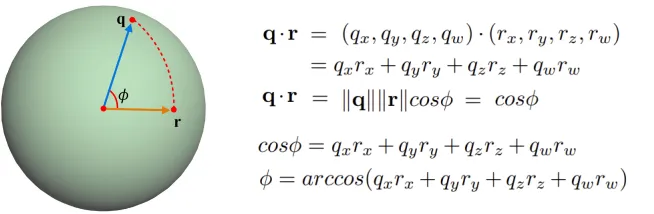
위의 interpolation 수식에서 sin값을 구하기 위해서 cos값을 구하는 방법을 설명해드리겠습니다. q와 r모두 단위 벡터이기 때문에 내적의 결과는 cos이고, 내적의 값은 좌표를 모두알고 있으니까 쉽게 구할 수 있습니다.
Quatarnian → Matrix
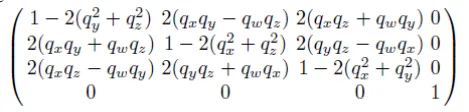
이전의 transform과 scaling matrix는 4x4 matrix이기 때문에 quaternion의 이전 sin에 관한 interpolation 수식도 4x4 matrix로 변환해야합니다. 변환결과는 위와 같습니다.
실제 사용 사례
3D Gaussian Splatting
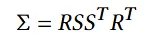
Covariance를 Rotation과 Scaling으로 나타냅니다. 이때 Scaling을 표현하는 방식이 Quaternian입니다.