출처: https://www.youtube.com/watch?v=c7la2Tt_cOc&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=13
한정현님의 컴퓨터그래픽스 12장 강의를 기반으로 제작한 블로그입니다.
Object Picking
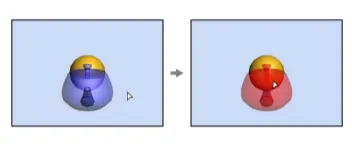
Screen space상에서 마우스로 물체를 클릭했을 때 이게 주전자에요! 아니면 이게 구에요! 라고 어떻게 구분할 수 있을까요? 지금까지 배운 정보만으로는 두 물체를 구분할 수 없습니다. 왜냐면 어떤 픽셀이 어떤 정보를 담고 있는지 알 수 없기 때문입니다.
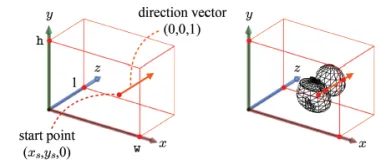
커서로 2차원에서 한 부분을 클릭했을 때의 위치를 start point로 나타내고, minZ=0, maxZ=1이라고 했을 때 start point에 해당하는 픽셀을 찾기 위해서 (0,0,1)방향의 벡터 ray를 쏘면 주전자 픽셀과 구 픽셀이 선택 될 것입니다. 하지만 이전에 말한것처럼 어떤 픽셀이 어떤 물체인지 알기 위해서는 우리는 object space상으로 다시 올라가서 확인해야하는 과정을 거쳐야 합니다.
Screen space → Camera space
Start point
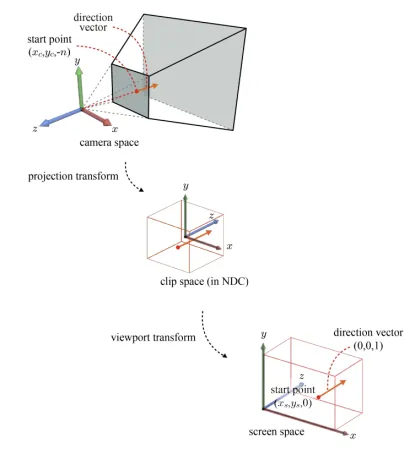
Object space로 한번에 넘어가는 과정은 힘드니 우선 Screen space → Clip space → Camera space로 변환하는 과정만 진행해보도록 하겠습니다.
커서의 위치 start point가 일 때 camera space에서 해당 위치를 이라고 해보겠습니다. z좌표가 -n인 이유는 view frustum의 첫번째 위치가 n만큼 떨어져있는데 z축의 음의 방향에 위치하기 때문에 -n으로 고정됩니다.

우리는 projection transform과 view port transform을 배운 상태이기 때문에 의 값에 2가지 변환을 거쳐서 start point 값을 구할 수 있습니다.
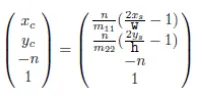
이를 반대로 에 대해서 나타내면 최종적으로 위와 같이 나타납니다.
direction vector
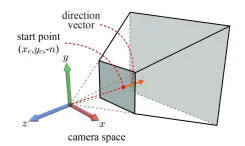
우리가 camera space에서의 start point를 찾은 상태입니다. Camera space에서 view frustum의 모든 벡터들은 원점을 향하도록 되어있는데 그러면 원점에서 start point로 향하는 벡터가 direction vector가 될 것 입니다.
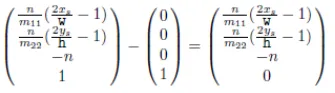
그래서 원점을 start point에서 빼주면 direction vector가 됩니다. 사실 w값이 1이냐 0이냐 차이밖에 없는데 1이면 점을 나타내고 0이면 벡터를 나타냅니다.
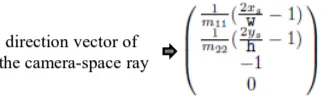
실제로 사용할 방향벡터는 모든 항에서 n을 나눠준 값입니다.
Camera space → World space
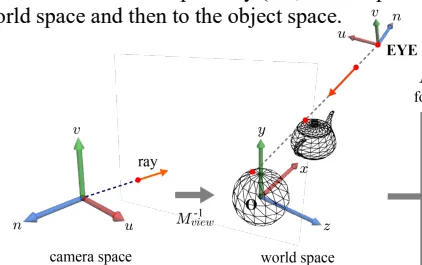
왼쪽의 Camera space에 있는 ray를 World space에서의 ray로 변환하기 위해서는 View transform의 역행렬을 취해야합니다. View transform이 RT이기 때문에 이의 역행렬은 입니다. 이를 통해서 ray를 world space로 변환할 수 있습니다.
World space → Object space
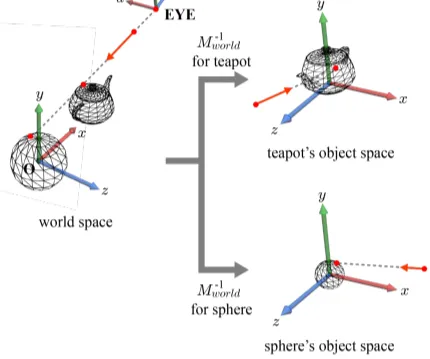
마지막으로 각 object space로 변환해주기 위해서 진행한 행렬(scaling, rotation, translation)의 역행렬을 진행하면 됩니다. 예를들어서 구같은경우 scaling을 2배취해서 크기가 커졌는데, 1/2배 취해서 크기를 줄이면서 구의 object space로 보냅니다. 그 결과 ray의 크기가 반으로 줄어든 것을 확인할 수 있습니다.

이렇게 각 object space로 ray를 변환해서 삼각형에 대해서 부딪히는지는 계산해야됩니다. 하지만 모든 삼각형에 대해서 계산을 하다보면 연산량이 많기 때문에 성능은 낮아지지만 빠른 방법인 bounding volume이 나왔습니다.
Bounding Volume
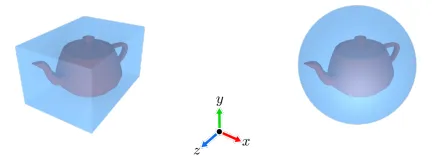
Bounding Volume은 크게 정육면체와 구 2가지 형태가 있습니다.
정육면체는 (X,Y,Z) 값에 대해서 Min, Max 값을 구하는 것이고, 구의 경우 중심과 반지름을 구하면 됩니다.
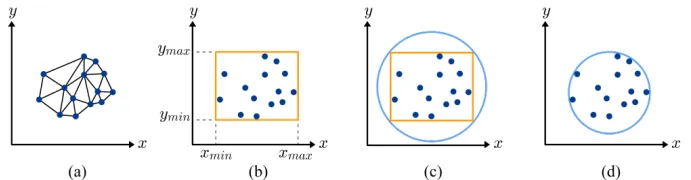
정육면체를 구하는 방법은 간단합니다. 모든 좌표에 대해서 (X,Y,Z)의 Min, Max 값을 구하면 되는 것이고, 구의 경우 해당 사각형의 외접원을 그리면 (c)의 결과가 나옵니다. 이때 더 정밀한 원 (d)를 얻는 방법도 존재하지만 알고리즘은 다루지 않았습니다.
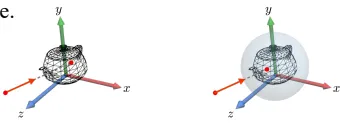
빠른 계산을 위해서 사용했지만 실제로 ray가 부딪히는 부분을 정밀하게 나타내지는 못합니다. 그래도 어느정도 근사화가 가능하기 때문에 실제로 부딪히는지 확인하는 방법을 알아보도록 하겠습니다.

우리가 ray에 대해서 시작점 의 값을 알고, ray의 방향 의 값을 모두 알기 때문에 direction vector를 알고 있고
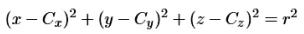
구의 방정식에 대해서 중심과 반지름을 모두 알기 때문에 x,y,z에 위의 vector를 대입해서 미지수 t만 풀면됩니다.
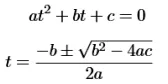
근의 공식을 통해서 쉽게 구할 수 있습니다.

값이 양수면 2개, 0이면 1개, 음수면 0개가 될 것입니다. 이때 값이 2개라면 작은 값(, 앞에 있는 값)을 선택하면 됩니다.
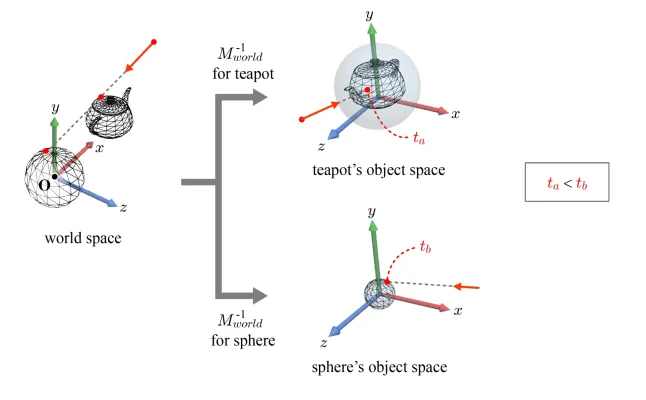
Ray가 부딪힌 순서를 정의하기 위해서 각 object space에서 나온 t값을 비교하면 됩니다. 당연히 작은 값이 앞에 있을 것이고 육안으로 봣을 때 주전자가 구의 앞에 있는데 실제로 t값도 주전자가 구보다 작게 나온 것을 확인할 수 있습니다.
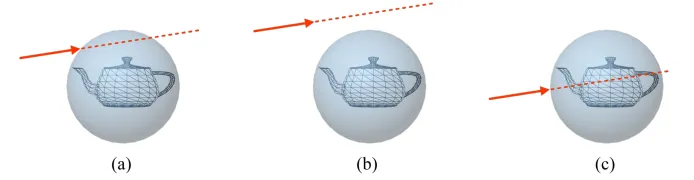
생각해보면 전처리로 Bounding volume을 사용하면 안되는 부분을 된다고는 하지만, 되는 부분을 안된다고는 안합니다. 따라서 부딪히는 후보를 찾기 위해서 사용한다면 좋은 전처리 방식이 될 것입니다.
Ray-Triangle Intersection
Bounding Volume을 통해서 대략적인 값을 구할 수는 있지만, 정확한 값을 구할 수 없었습니다. 따라서 정확한 값을 구하기 위한 방법 Ray-Triangle Intersection을 설명해드리겠습니다.
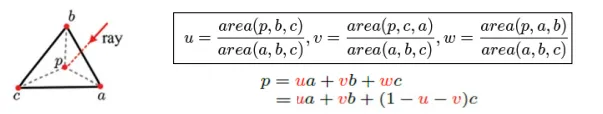
Ray(p)가 삼각형 안에 존재한다면 p에 따라서 삼각형의 꼭짓점 a,b,c에 대한 가중치 u,v,w를 넓이로 나타낼 수 있습니다. 고등학교 수학시간에 배웠던거같기도 한데 그냥 직관적으로 p의 값이 a쪽으로 갈수록 u의 넓이가 커질 것이고, 그러면 p에 대해서 a의 영향력이 커질 것입니다.
u+v+w = 1이고, w를 1-u-v로 나타내면 최종적으로 위와 같은 수식이 나옵니다.
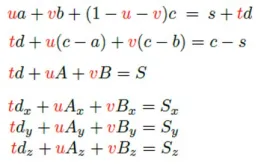
ray에 대한 수식 s+td를 알고, 방금 구한 수식 ua + vb + (1-u-v)c를 알기 때문에 2개의 벡터에 대해서 접점을 구하면 됩니다. 마지막처럼 방정식이 3개고 미지수가 3개이기 때문에 t,u,v를 구할 수 있습니다.
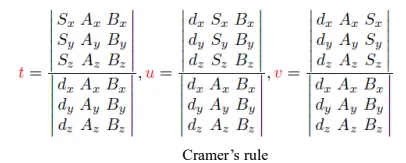
Cramer 공식을 쓰면 한번에 구할 수 있다고 하셨는데 처음 듣는 공식이었고… 어차피 컴퓨터가 해줄테니까 그냥 듣고 넘어갔습니다.
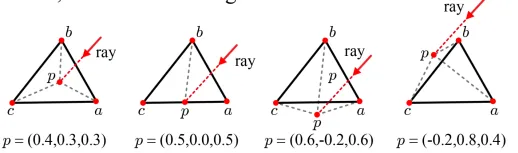
u,v,w중 하나라도 음수 값이 나오면 p의 점이 삼각형의 밖에 존재하게 됩니다.
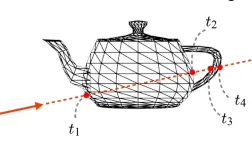
참고로 여러개의 t값이 나오게 된다면 가장 작은 값을 선택하면 됩니다.
Arcball
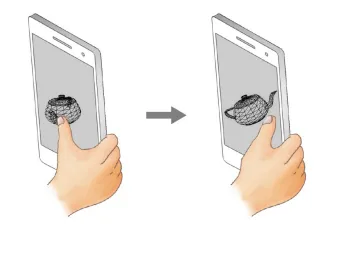
화면 상에서 주전자를 손가락으로 회전시키거나 이동시켰을 때 변화를 나타나게 하려면 어떠한 기술이 적용되는지 확인해보도록 하겠습니다.
알고리즘은 간단합니다. 물체(주전자)를 감싸고 있는 구가 있다고 할 때 구의 회전을 통해서 물체의 회전을 나타냅니다. 이때 물체를 감싸는 구를 archball이라고 합니다.
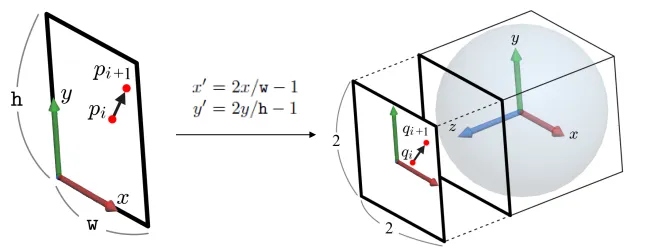
효율적인 실행을 위해서 구를 3차원공간의 중심으로 이동 시키고 반지름을 1로 변환하기 위해서 새로운 좌표 x’,y’를 구합니다. 범위가 [0,w]였는데 [-1,1]로 변환하기 위해서 w로 나눠주고 → 2를 곱하고([0,2]) → 1을 빼주면 [-1,1]의 범위가 나옵니다.
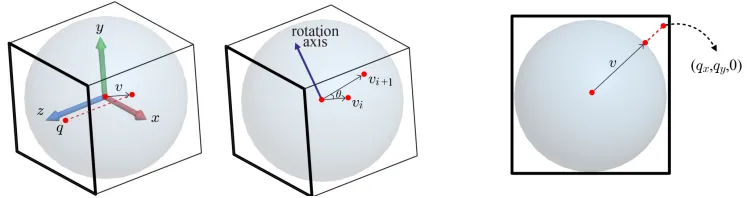
이렇게 새로운 좌표에서의 좌표를 q라고 했을 때 arcball에 투영하면 z축을 따라 이동하게 될 것입니다.
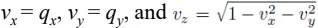
이때 투영된 점 v는 x와 y좌표가 q와 동일할 것이고, 반지름은 1이기 때문에 각 점의 값은 위와 같을 것입니다.
참고로 오른쪽 그림과 같이 원의 밖에 존재하는 경우도 존재하는데, 이때는 단순히 xy평면에 projeciton한 결과를 normalize해서 길이를 1로 만들어줍니다.
그리고 가운데 그림에 보이는 것처럼 가 로 이동할 때 회전 축과 각도가 필요합니다. 이때 회전 축은 와 과 수직일 것이기 때문에 와 을 외적한다면 회전축을 구할 수 있을 것입니다.
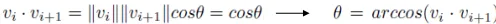
마지막으로 각도를 구하기 위해서 위의 수식처럼 내적을 이용해서 단위벡터를 제거하면 쉽게 각도를 구할 수 있습니다.
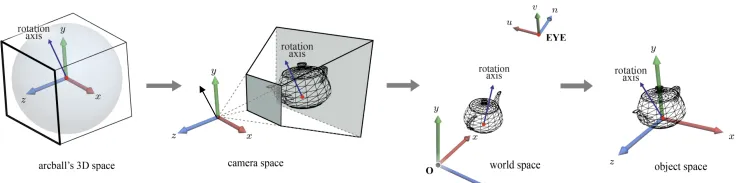
물체의 회전을 표현하기 위해서 arcball을 이용해서 나타내려고 지금까지 살펴봤습니다. 결론적으로 축과 각도를 구했으므로 이를 objet space로 이동해서 다시 변환을 적용해야합니다.
지금 정의된 arcball space라는 것은 없기 때문에 이를 object space로 변환할 때 트릭을 사용해야합니다. Arcball이라는 것 자체도 어쨌든 우리의 눈(카메라)를 통해서 보인다고 가정했기 때문에 이를 camera space의 공간으로 그대로 옮겨도 문제가 없습니다. 그래서 회전축 자체를 camera space로 변환하고 이를 다시 world space 그리고 마지막으로 object space로 보내면 됩니다. 참고로 각도는 상수이기 떄문에 변환하지 않아도 됩니다.
회전축과 각도를 이용해서 행렬을 만드는건 Open GL의 glm 라이브러리를 이용하거나, 11장에서 배운 축(u)를 중심으로 quantarian을 이용하는 방식 2가지가 있을겁니다.
이렇게 행렬을 구해서 object space상에서 변환을 진행하고 이를 다시 world space → camera space .. 과정을 진행하게 됩니다.
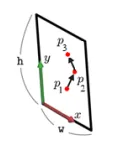
이렇게 p1에서 p2로의 변환을 나타냈는데, p2에서 p3의 새로운 변환이 있을 때는 당연히 이전 행렬을 곱해서 새로운 위치를 구하고 해당 위치에서 다시 새로운 행렬 변환을 곱해줘야합니다. 이전꺼를 생략하게 되면 전혀 다른 위치에 존재하게 될 것입니다.
