출처: https://www.youtube.com/watch?v=gCcJ6GzZpWY&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=15
한정현님의 컴퓨터그래픽스 14장 강의를 기반으로 제작한 블로그입니다.

Normal Mapping

Normal Map

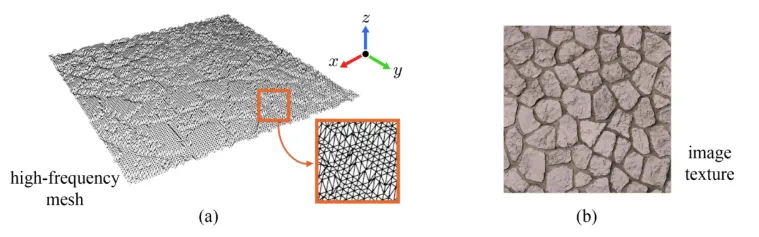
왼쪽과 같이 오돌토돌한 형태의 high-frequency mesh에 image texture를 입히면

위의 그림이 나올 것 입니다. Image texture랑 비교했을 때 굉장히 사실적인 결과가 나온 것을 확인할 수 있습니다. 어떻게하면 이렇게 오돌토돌하게 사실적으로 나왔는지 자세히 살펴보도록 하겠습니다.

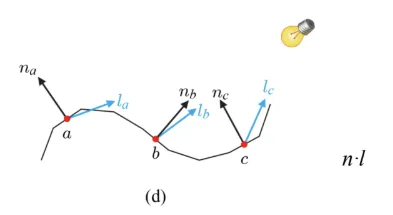
한 부분을 확대했을 때 이렇게 여러개의 점으로 나타나 있고, 각 점들의 normal은 다양한 방향이로 존재합니다. 이 때 a와 c는 이전 라이팅에서 배운 n과 l의 내적 값이 작기 때문에 빛이 약하게 반사될 것이고, b점은 내적 값이 크기 때문에 빛이 강하게 반사될 것입니다. 작은 공간에서 밝기가 달라지면서 이전 그림처럼 오돌토돌한 결과가 나타나게 됩니다.

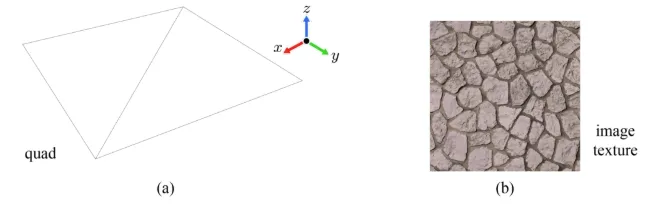
반면에 low-frequency mesh에 이미지 텍스처를 적용하면

위의 그림과 같이 밋밋한 결과가 나올 것 입니다. 그러면 어떻게 low-frequency 처럼 시간을 적게 들인 결과를 이용해서 high-frequency와 같이 좋은 결과를 얻을 수 있을까요?

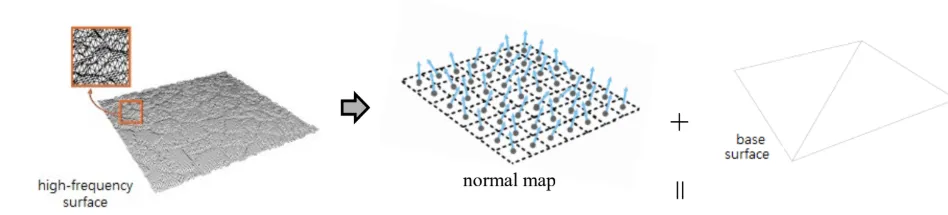
방법은 간단합니다 high-frequency의 normal 정보를 저장한 normal map을 이용하고 실제 surface는 low-frequency를 사용하는 것입니다. 왜냐하면 빛을 계산할 때는 결국 normal 정보만 이용하기 때문입니다.

Height Map

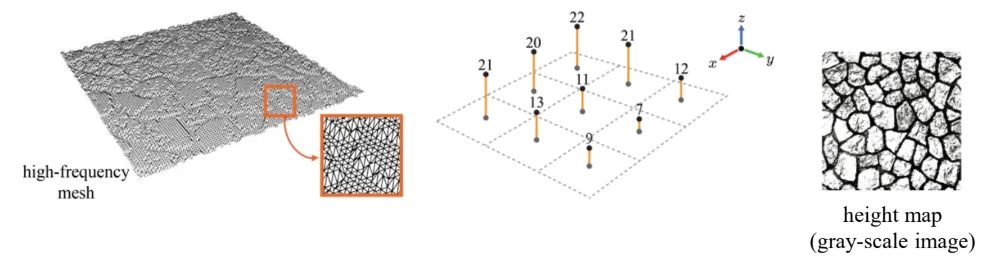
Normal map을 만들기 위해서는 height map이 필요합니다. Height map은 h(x,y)의 함수를 이용해서 (x,y)의 위치에서 z값인 height값을 어떻게 나타내는지에 대해서 저장한 정보입니다.

위로 튀어나온 돌이 있다면 height가 높을 것이고, 평평하다면 height가 낮을 것입니다. 값이 큰 값일수록 흰색을, 작을수록 검정색을 띕니다.

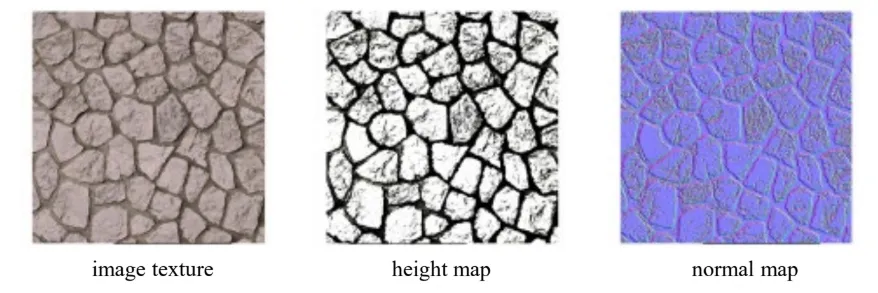
방금 설명에서는 surface에서 height map을 생성하는 방법을 배웠는데, 사실 image texture에서 바로 height map을 생성할 수 있습니다. Image texture의 r,g,b값을 다 더해서 3으로 나눈 후 grayscale로 표현하면 height map이 나옵니다. 이때 가운데 부분의 어두운 돌 부분은 실제로 높이 위치하지만 어두워서 height map이 작게 나온 것이므로 이렇게 잘 안나온 부분은 사람이 포토샵으로 후처리 과정을 거치면서 height map을 생성하게 됩니다.

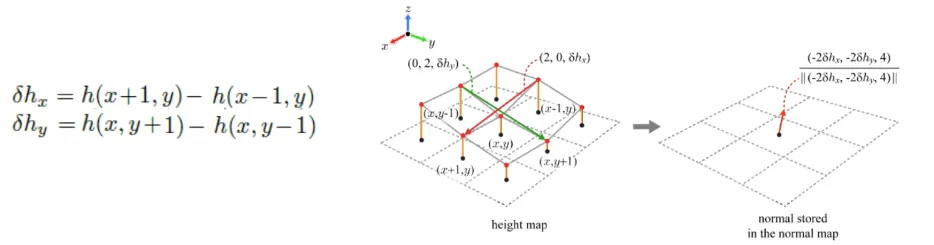
최종적으로 우리는 height map을 통해서 normal map을 얻고 싶습니다. 우리가 가운데 점 (x,y)의 normal map을 얻기 위해서 3x3 height들을 이어서 사각형을 만들고 사각형의 normal을 구하면 대충 해당 점의 normal과 비슷할 것 입니다.

사각형의 normal을 구하기 위해서 중심 (x,y)에서 x축으로 +1과 -1한 좌표의 height 점을 이용해서 빨간 벡터를 구하고, 마찬가지로 y축으로 +1과 -1한 좌표의 height 점을 이용해서 초록 벡터를 구합니다. 빨간 벡터와 초록 벡터의 외적을 진행하면 사각형의 normal을 대략적으로 얻을 수 있게 됩니다.

만약에 9개의 점이 사각형을 이루지 않는다면 해당 점을 기준으로 x축 +1,-1, y축 +1,-1 4개의 점을 이용해서 삼각형 4개의 normal vector를 정규화 해서 (x,y)의 normal vector를 생성합니다.

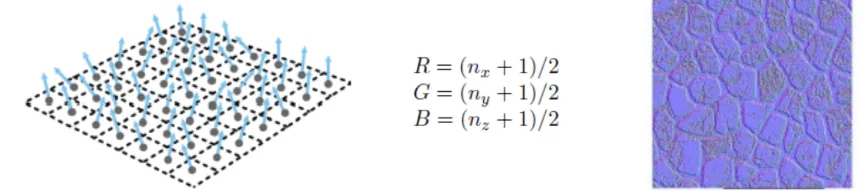
마지막으로 방금 구한 정규화된 normal vector는 [-1,1] 범위를 갖고, texture map은 [0,1] 범위를 갖기 때문에 두 범위를 일치시키기 위해서 위의 수식을 진행하면 최종적인 normal map을 얻게 됩니다.

Normal map을 보면 거의 파란색을 띄는데, 일반적으로 normal map이 z축 방향으로 나타나 있기 때문입니다.

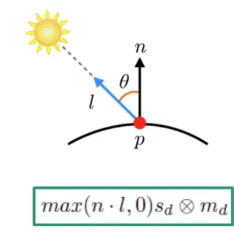
이렇게 얻은 normal map을 이용해서 lighthing 정보도 얻을 수 있습니다.

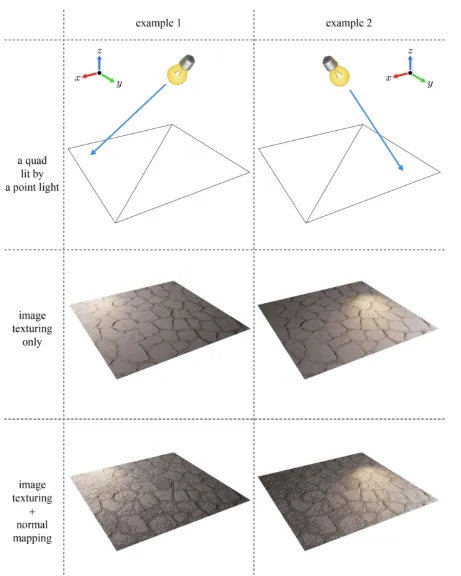
결론적으로 그냥 image texture를 사용한 결과보다 normal mapping 까지 한 결과가 훨씬 더 사실적인 묘사가 가능합니다.

Tangent space

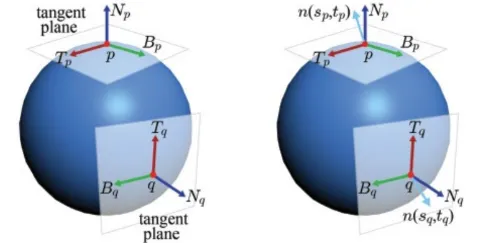
만약에 Normal map이 존재하지 않았다면, lighting을 계산 하기 위해서 구의 한 점에서의 normal 값을 이용 했을 것 입니다. 그러면 한 점에서 3개의 벡터를 한번 생각해보도록 하겠습니다. 구에 접선인 T, 구에 접선이면서 T에 수직인 B, 그리고 normal N을 정의했습니다. 3가지 벡터는 서로 수직이기 때문에 orthonormal basis이고, 이 공간을 tangent space라고 하겠습니다. 이때 우리가 normal map으로 구한 normal은 (0,0,1) 근처의 값일 것이고 시각화하면 오른쪽 그림의 하늘색 벡터일 것입니다. 따라서 normal map의 각 정점의 normal 값들은 각 정점의 tangent space에서 정의 됐다고 할 수 있습니다.

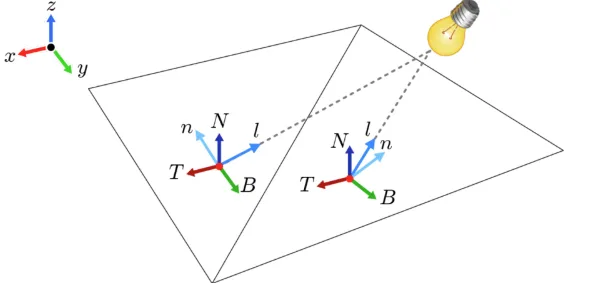
갑자기 왜 tangent space를 정의했는지 설명해드리도록 하겠습니다. Lighting을 계산하기 위해서 우리는 normal과 light를 내적을 취해야하는데, light는 world space에서 정의 됐고 normal은 방금 tangent space에서 정의 됐다고 했습니다. 서로 다른 space의 벡터의 내적을 진행할 수 없기 때문에 공간을 통일시키는 과정이 필요합니다. 이를 위해서 light를 tangent space로 변환하도록 하겠습니다.

T,B,N 3개의 벡터들은 object space에서 정의 됐기 때문에 이를 view transform을 이용해서 world space로 변환해보겠습니다. 이후 world space의 basis인 u,v,n을 world space로 변환된 tangent space T,B,N과 일치시키는 변환을 진행하도록 하겠습니다.

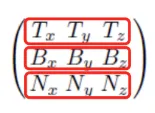
이전에 배운 view transform 과정과 동일하게 축의 중심을 일치(translation)시키고, 방향을 일치(rotation)시키면 됩니다. View transform은 u,v,n의 좌표를 transpose해서 썼으므로 동일하게 T,B,N의 좌표를 transpose 하는 과정이 행렬 식이 될 것입니다.