출처: https://www.youtube.com/watch?v=aZcrHIDO5zY&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=14
한정현님의 컴퓨터그래픽스 13장 강의를 기반으로 제작한 블로그입니다.

Character Animation

Skeleton

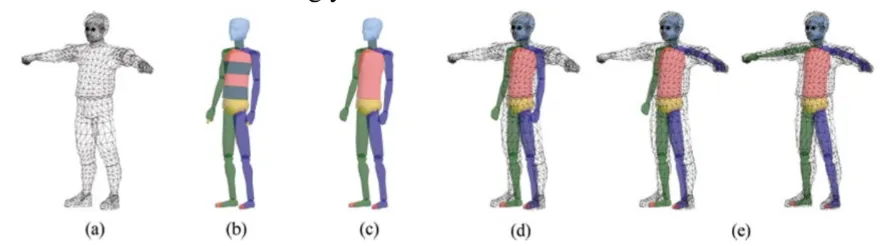
애니메이션에서 캐릭터를 표현하는 가장 유명한 방법은 스켈레톤을 사용하는 것 입니다. 스켈레톤의 팔이나 다리 같은 요소들은 개별적으로 움직이기 때문에 관절체(articulated body)라고 불립니다. 위의 그림은 스켈레톤을 캐릭터와 일치시키는 Rigging 과정을 나타냅니다.

Rigging 과정

(a): Default(Dress) pose 형태로 initial pose를 가진 캐릭터가 생성

(b): 3D 소프트웨어 Max가 biped라는 스켈레톤 제공

(c): 뼈의 개수를 사용자가 설정(b → c로 변환될 때 더 적어짐)

(d): 캐릭터와 스켈레톤을 맞춥니다.

(e) & (f): 변환을 통해서 2요소를 일치시킵니다.

왜 스켈레톤을 사용해야해?

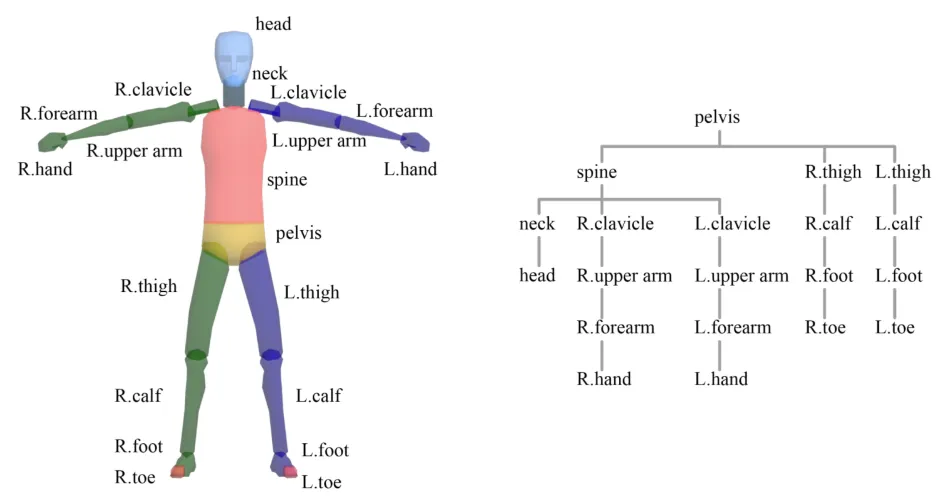
실제 그래픽스 강의에서 사용하는 스켈레톤입니다. 20개로 이루어져있고, 골반(pelvis)를 기준으로 부모자식 관계를 갖고 있습니다.

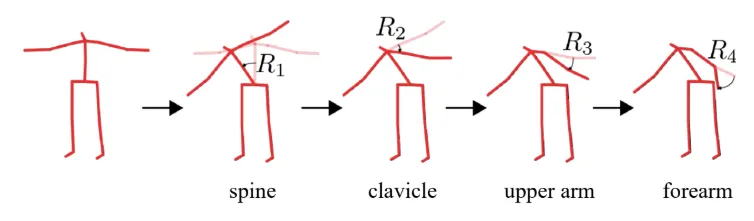
관절체를 다루기 어려운 이유는 개별적으로 움직이기는 하지만 각 요소들의 움직임이 다른 요소에 영향을 주기 때문입니다. 위의 사진을 보시면 맨오른쪽에 R4 회전이 오른손 팔을 45도만 회전했을 결과인데, 이전 몸의 위치가 변화했기 때문에 단순히 45도 회전한 결과보다 더 아래에 있는 결과가 나온것을 확인할 수 있습니다.

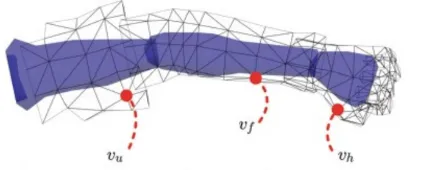
오른쪽 팔들은 이전에 봤던것처럼 3개의 부분공간으로 나눌 수 있고, 각 부분 공간들은 개별적으로 움직이기 때문에 각각의 좌표 공간이 필요합니다.

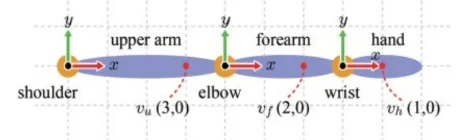
2차원 형태로 나타내면 위와 같습니다. 모든 뼈들은 각각의 좌표 공간이 필요하고, 이를 하나로 정의한게 기존의 object space였습니다. 따라서 Object space안에서 뼈들을 위한 좌표공간과 캐릭터 좌표 공간 2가지가 혼동되기 때문에 이를 bone space와 character space로 명명했습니다.

우리의 최종적인 목표는 character space 상에 존재하는 좌표들이 각각의 bone space에서 어떤 좌표에 해당하는지, 즉 character → bone space로의 변환 결과를 원합니다.

To-parent transform

하지만 일단 설명을 위해서 bone → character space로 변환을 먼저 배워보도록 하겠습니다. 첫번째로 해야되는 작업은 여러개의 bone space를 하나로 합치는 과정입니다. 위에 3개의 bone space(upper arm, forearm, hand)가 있는데 이를 가장 높은 계층(부모 노드)인 upper arm의 공간으로 변환하는 to-parent transform 과정을 살펴보겠습니다.

forearm에서 (2,0)인 좌표는 upper arm에서 (6,0)일 것입니다. 왜냐면 forearm의 원점이 upper arm 기준에서 (4,0)이기 때문입니다. 이와 같이 to-parent transform은 2개의 좌표를 일치시키기 위해서 view transform(world space → camera space)의 변환처럼 translation으로 원점을 일치시키고 rotation으로 좌표의 방향을 일치시키는 과정을 진행하면 됩니다.

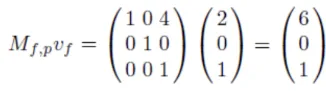
forearm이 upper arm으로 변환되는 과정을 수식으로 나타내면 위와 같습니다. 단순히 (4,0) translation을 진행하면 됩니다.

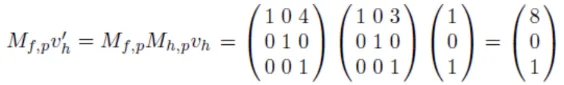
hand는 upper arm이 되기 위해서 forearm을 거쳐야 하기 때문에 위와 같은 2번의 변환이 필요합니다. 결론적으로 모든 bone space는 자신의 parent로 변환하는 to-parent transform이 가능합니다.

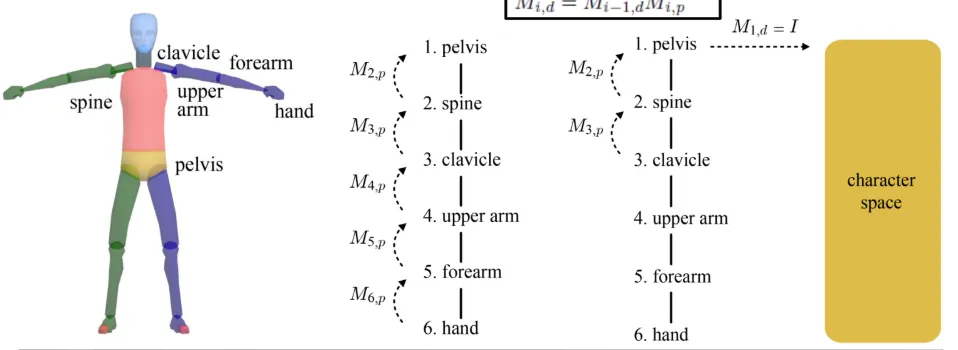
이전에 봤던 to-parent transform은 최종적으로 골반(pelvis)로의 변환으로 모든 bone space를 통일시킬 수 있습니다. 계층적으로 i번째 위치하는 뼈에 대해서 to-parent transform은 $M_{i,p}$로 나타낼 수 있습니다.

골반의 공간 자체가 character space랑 동일하기 때문에 모든 뼈들을 골반의 공간으로 변환하면 bone → character의 변환이 가능하게 됩니다. 이렇게 i번째 뼈에서 character로 변환되는 행렬을 $M_{i,d}$라고 합니다.

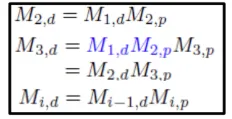
2번째 계층의 뼈공간에서 캐릭터 공간으로 변환하기 위해서는 첫번째로 골반으로의 변환 $M_{2,p}$를 진행하고, 이후에 character space로의 변환 $M_{1,d}$를 진행합니다. 위의 나머지 예시들도 쉽게 이해할 수 있을 것 입니다. 마지막 수식은 계속 올라가는 과정을 간단하게 부모한테 가면 부모는 캐릭터로 가는 방법을 알고 있기 때문에 부모한테까지만 가면된다는 것을 나타내는 것 입니다.

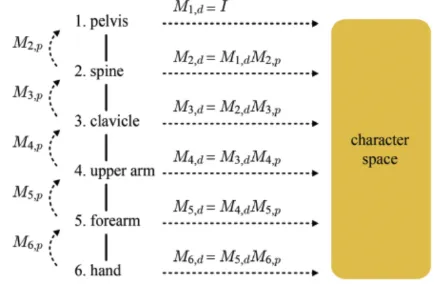
위의 그림처럼 우리는 bone → character space의 변환을 모두 진행할 수 있게 됐습니다.

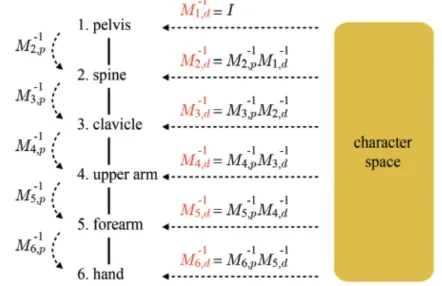
그러면 최종적으로 우리가 원하는 character → bone space로의 변환을 역행렬을 통해서 구할 수 있게 됩니다.

Forward Kinematics

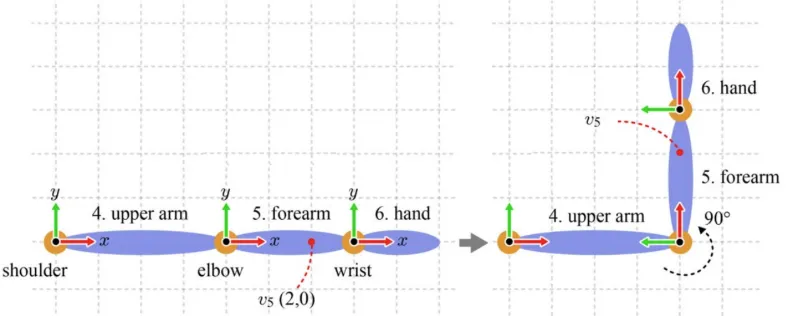
우리가 팔을 90도 구부려서 forearm의 $v_5$의 정점이 위로 움직였다고 해보겠습니다. 이와 같은 애니메이션을 표현하기 위해서 우리는 character space를 bone space로 변환했습니다. 이제 이 과정을 사용자에게 보여주기 위해서 rendering을 한다고 했을 때 우리는 world transform(object→ world space) 변환을 진행해야합니다. 하지만 여기서 말하는 object는 character space이기 때문에 현재 우리가 있는 bone space에서 다시 character space로 변환해 줘야 합니다.

즉 우리는 character space → bone space(애니메이션을 표현하기 위해서) → character space(랜더링 하기 위해서) 과정을 진행해야 합니다. 이렇게 2가지 변환을 우리는 $M_{i,a}$의 행렬로 나타낼 수 있습니다.

Rotation, Translation, Scaling 중에서 뼈는 Rotaiton 행렬만을 이용합니다. 당연히 태권브이처럼 팔이 날라가지 않기 때문에 translation은 없고, 헐크처럼 뼈가 커지지 않기 때문에 scaling은 없습니다. 따라서 local transform은 rotation밖에 없고 이를 $M_{i,l}$의 행렬로 나타냅니다.

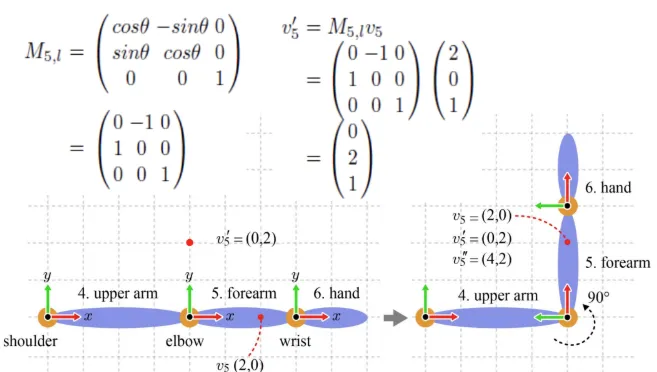
그래서 회전행렬을 취해서 $v_5$가 (2,0)에서 (0,2)로 변환이 됐습니다. 이 변환은 forearm space에서의 변환이 일어난 것이고, 이를 character space로 변환하기 위해서는 다시 parent space로 변환해줘야 합니다.

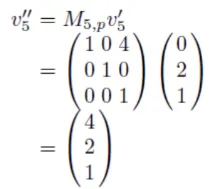
우리는 이전에 parent space로 변환하는 행렬을 위와 같이 알고 있기 때문에 최종적으로 (4,2)라는 좌표값을 얻을 수 있습니다.

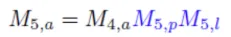
(2,0) → (0,2)로의 변환은 $M_{5,l}$, (0,2) → (4,2)로의 변환은 $M_{5,p}$로 나타냈었습니다. 우리가 최종적으로 원하는건 $M_{5,a}$인데 이건 parent 4의 $M_{4,a}$를 곱해야 알 수 있습니다. 지금 부모 노드의 공간으로 변환은 했지만, 부모가 아직 애니메이션을 어떻게 적용할지는 모르는 상태인 것입니다.

그렇다면 위의 4입장에서도 3,2,1의 정보를 알아야 변환이 가능하겠죠? 이런식으로 이전 모든 정보를 알 수 있다면 모든 정보를 쉽게 계산할 수 있게 됩니다.

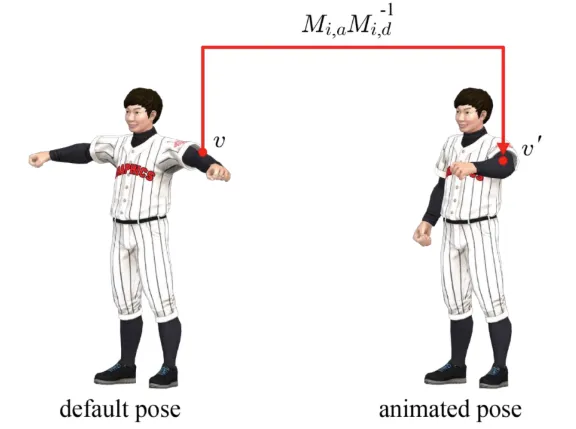
이제 우리는 default pose에서 어떠한 동작이 취해진 결과를 bone space로 변환해서, 이를 다시 character space로의 변환을 통해서 animated pose를 얻을 수 있습니다.

Skinning

하나의 점이 하나의 born space에만 속한다고 가정했을 때 변환된 결과는 오른쪽과 같지 부드럽지 않은 결과가 나타납니다.

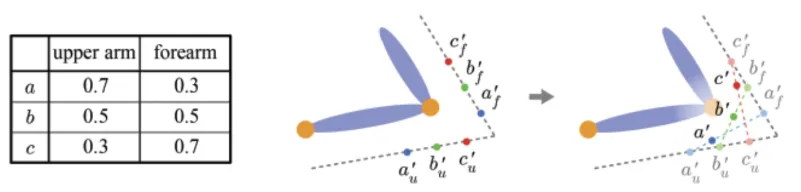
이러한 문제를 해결하기 위해서 하나의 점이 여러개의 born space에 속하고, 어떤 born space에 더 많이 속할지 비율을 정해보도록 하겠습니다.

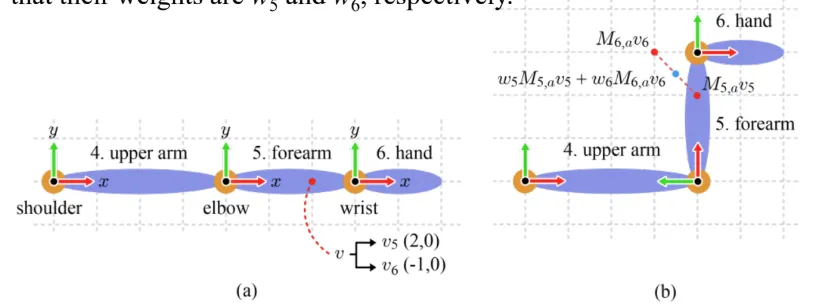
예제를 통해서 다시 한번 자세히 설명해보도록 하겠습니다. v라는 점이 forearm과 hand에 속한다고 했을 때 우선 이를 각각의 born space로 변환해서 (2,0)과 (-1,0)이라는 좌표를 얻었습니다. 이후 animation을 적용하고, 가중치에 따라서 interpolation된 결과를 다시 character space로 변환합니다.

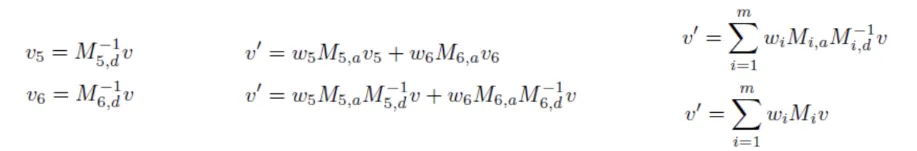
방금 설명한 과정을 수식적으로 나타내면 위와 같습니다.

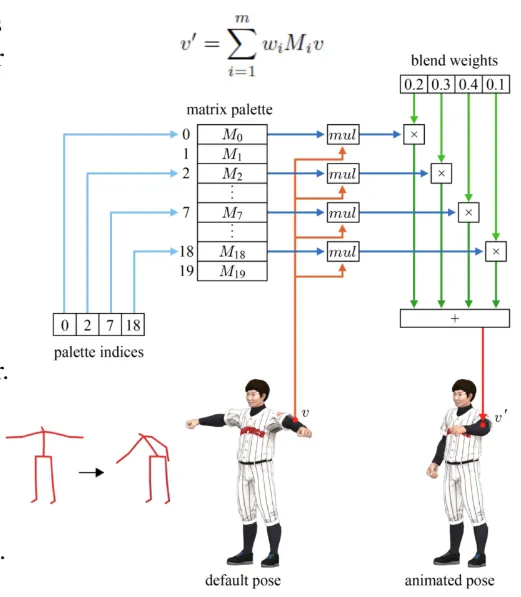
애니메이션을 진행할 때 우리가 20개의 뼈를 부분내서 고려한다면, M행렬 역시 20개가 필요할 것입니다. 그리고 이전에 설명한 하나의 점이 영향을 받는 벼들은 기본적으로 4개로 설정합니다. 4개의 뼈들은 프레임 마다 다른 가중치로 영향을 줄 수 있지만, 이 4개의 뼈가 바뀌는 일은 없습니다.

정리하면 매 frame마다 born space로의 변환을 나타내는 M값들을 저장하는 matrix palette가 정의 될 것이고, 각 정점마다 4개의 점의 정보를 나타내는 palette indices와 4점의 가중치를 나타내는 blend weights 값을 받을 것 입니다.

Keyframe + Skeletal Animation

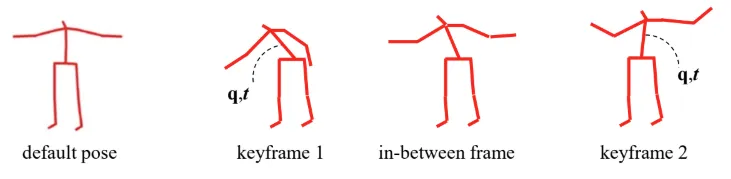
이전 강의에서 설명한 Keyframe에 대해서만 표현이 정의되어 있기 때문에 $M_{i,a}$행렬은 Keyframe에만 존재하고, in-between frame은 interpolation을 통해서 구해야 합니다.

Interpolation을 설명하기 위해서 $M_{i,a} = M_{i-1,a}, M_{i,p}, M_{i,l}$의 수식을 살펴보도록 하겠습니다. $M_{i,l}$은 local 변환이므로 rotation 만을 나타내고, $M_{i,p}$는 좌표 변환이기 때문에 rotation과 translation 만을 나타냅니다. 따라서 $M_{i,a}$행렬 자체는 rigid transform(강체 변환)인 [R|t]로 나타낼 수 있습니다. 이전강의에서 우리는 interpolation을 정확하게 나타내기 위해서 Rotation은 quaterninon으로 나타내야 합니다.

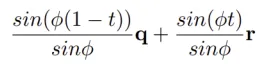
Quaterninon은 위와 같이 interpolation을 진행했었고, quaternion의 interpolation의 계산 결과도 quaternion이었습니다.

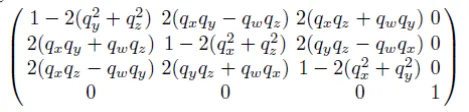
따라서 위와 같이 quaternion을 matrix로 바꿔주고, 마지막 4번째 열에 대해서 translation 값을 더해줘서 최종적인 interpolation 과정을 진행합니다.

Inverse Kinematics

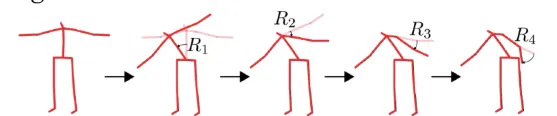
우리가 끝 결과를 알고 있을 때, 각각의 뼈들이 어떻게 변하는지를 역으로 파악하는 과정을 Inverse kinematics(IK) 라고 합니다.

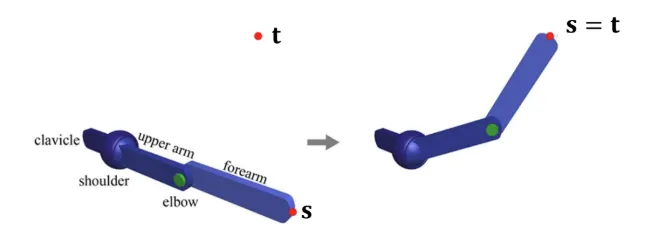
위의 그림과 같이 로봇이 어떤 물체를 들기위해서 팔의 위치를 변환했다고 했을 때 어떤 변환이 일어나는지 확인해보도록 하겠습니다.

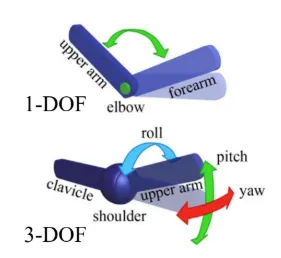
팔같은 경우 회전하는 경우만 고려하기 때문에 물체의 상태를 정의하는 변수 degrees of freedom(DOF)는 1, 어깨의 경우, 좌우 상하로 움직이고 어깨 뼈 자체가 움직일 수 있기 때문에 DOF는 3입니다.

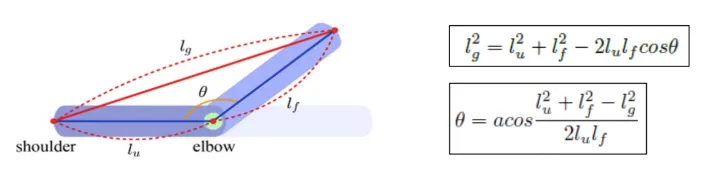
DOF가 1인 팔의 움직임을 나타내는 경우는 팔의 길이 자체는 고정되어 있기 때문에 코사인 법칙을 이용해서 각도라는 변수를 얻을 수 있습니다.

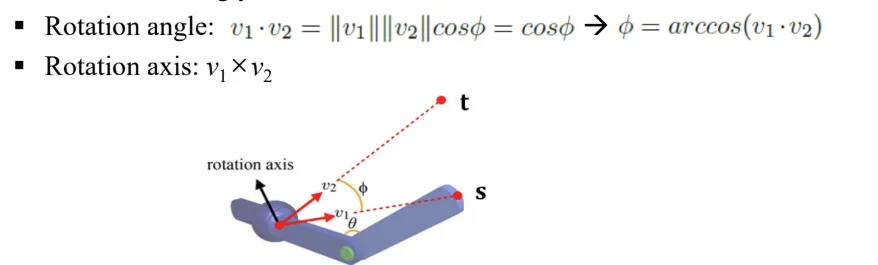
DOF가 3인 경우 s를 t만큼 회전시킨 결과를 얻기 위해서 arcball 방식을 사용합니다.

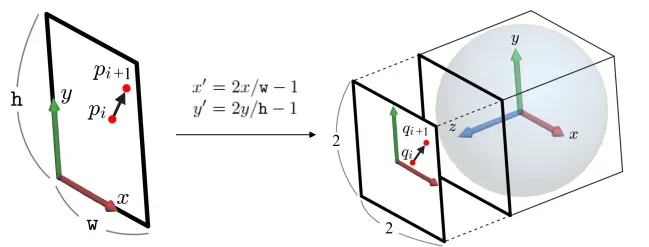
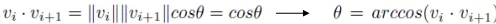
Arcboll은 12장에서 나온 개념으로 두 벡터의 변환을 나타낼 때 구를 이용해서 대략적인 변환을 가능하게 했습니다.

Cyclic Coordinate Descent

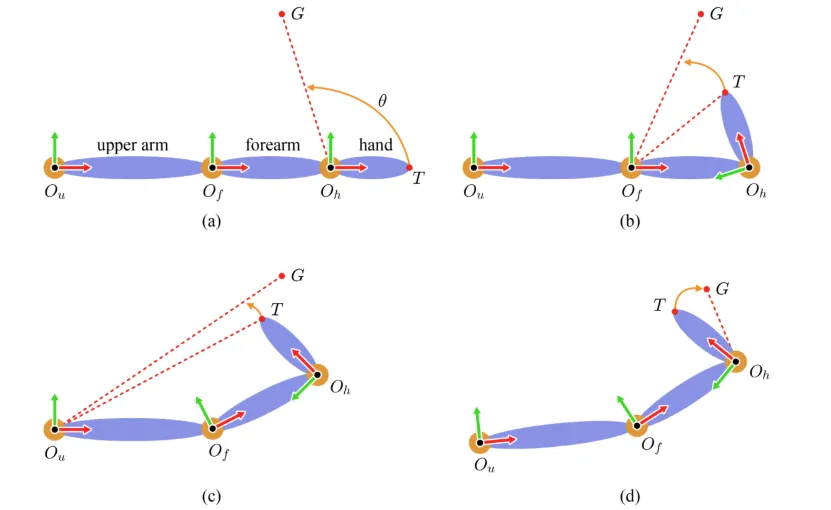
방금 설명한 과정을 leaf노드에서부터 반복하는 과정을 CCD(Cyclic Coordinate Descent)라고 합니다. (a)과정에서 hand를 G방향으로 이동하고 여전히 부족하기 때문에 (b),(c) 과정에서도 forearm과 upper arm을 수정하게 됩니다. 이후에 (d)과정에서 다시 leaf 노드로 돌아와서 최종적으로 회전하게 됩니다.