[한정현 컴퓨터 그래픽스] 2장 수학 기초

출처: https://www.youtube.com/watch?v=774mc7tC594&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=3
한정현님의 컴퓨터그래픽스 2장 강의를 기반으로 제작한 블로그입니다.

앞부분의 행렬과 벡터에 대해서는 생략하고 컴퓨터 그래픽스에 필요한 수식중 개인적으로 까먹었던 내용에 대해서만 간략하게 정리했습니다.

Coordinate System and Basis

Coordinate system(공간) = origin(원점) + basis(기저)

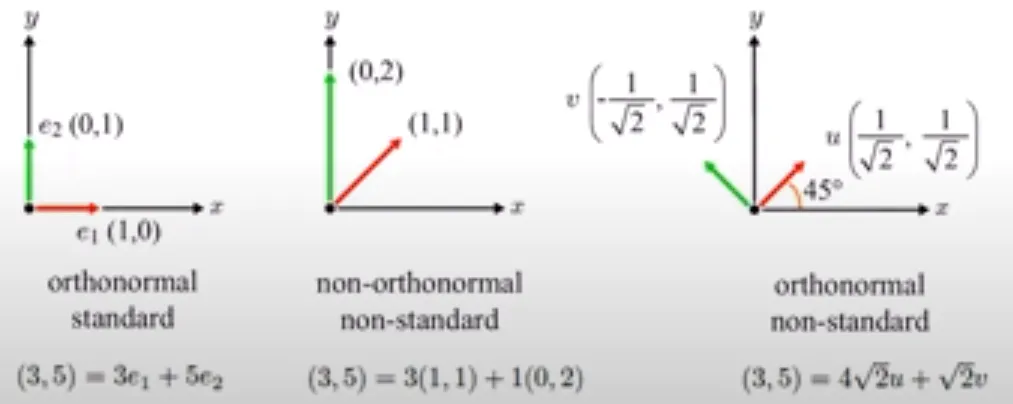
맨왼쪽에 나와있는 2차원 공간에서 basis는 e1(1,0)과 e2(0,1)입니다. 해당 basis는 standarad basis라고 부르는데 2개의 basis로 모든 2D 공간을 나타낼 수 있기 때문입니다. 또한 standard basis는 orthonomal(orthogonal(직각) + normalize(단위가 1))

가운데에 있는 e3(1,1), e4(0,2)도 basis로 나타낼 수 있지만, standard basis는 아닙니다.

맨 마지막에 있는 basis처럼 standard basis는 아니지만 직각을 이루고, 길이가 1인 orthonormal basis를 만들 수 있습니다.

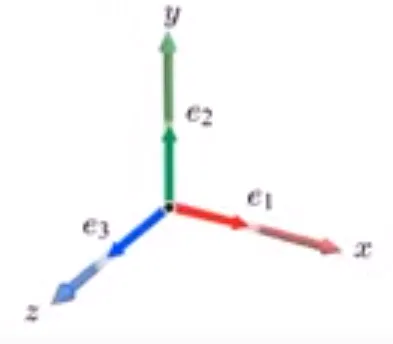
이번에는 3차원에서 3개의 basis e1(1,0,0), e2(0,1,0), e3(0,0,1)를 이용해서 나타낼 수 있습니다. 3개의 basis는 3차원 standard basis입니다.

Cross Product

내적과 달리 외적(Cross Product, x)는 3차원에서만 정의됩니다. 벡터 a와 b의 외적은 새로운 3차원 벡터를 얻게 됩니다.

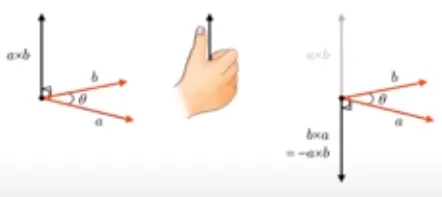
새로운 벡터의 방향은 오른손 법칙에 의해서 정의됩니다. 따라서 axb와 bxa의 방향은 반대가 됩니다.

새로운 벡터의 길이는 |a||b|sin$\theta$이고, 이는 평행사변형의 넓이로 나타낼 수 있습니다.

만약 a=b(방향과 길이가 모두 같은 벡터)이면 axb(a와 b의 외적)은 0이됩니다.

Line, Ray, and Linear Interpolation

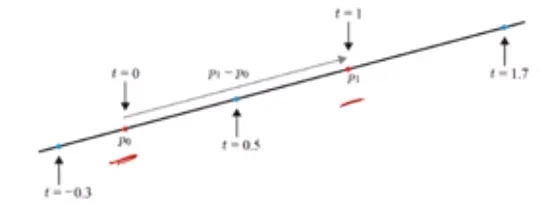
$p(t) = p_0 + t(p_1 - p_0)$ → $p_0$에서부터 $p_1$까지 무한히 잇는 직선

• t=0 일 때 $p_0$, t=1일 때 $p_1$

Ray: [0, $\infin$]로 p(t)의 범위를 제한한 직선

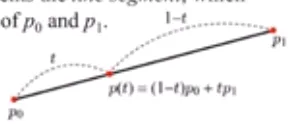
$p(t) = (1-t)p_0 + tp_1$ → t가 [0,1]범위 안에 있을 경우 p(t)는 $p_0$와 $p_1$사이의 값으로 제한됩니다. 이는 선형보간(linear interpolation)이라고 합니다.