출처: https://www.youtube.com/watch?v=CAfdIW8M6HA&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=6
한정현님의 컴퓨터그래픽스 5장 강의를 기반으로 제작한 블로그입니다.
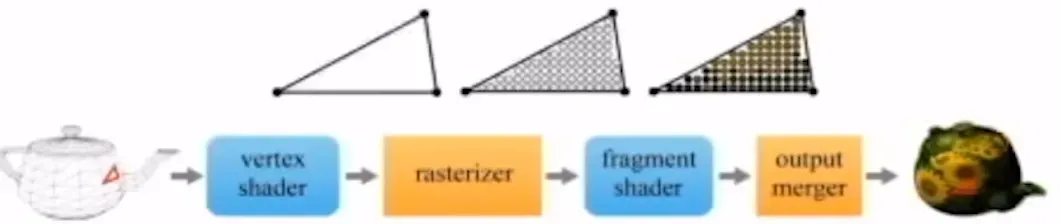
GPU Rendering Piepline
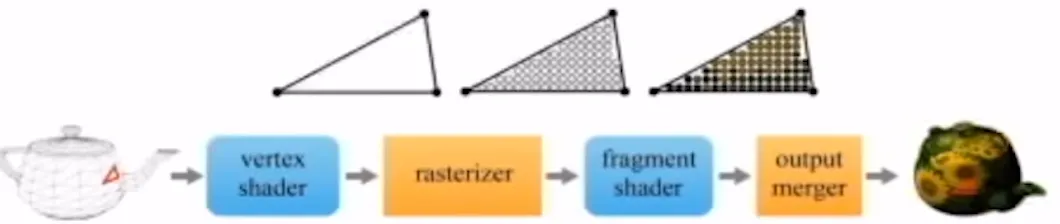
Vertex array: 주전자의 각 점들이 저장된 정보
Vertex shader: 정점들을 하나씩 가져와서 여러 연산들을 수행
rasterizer: index array 정보를 이용해서 삼각형을 다시 조립
- 맨왼쪽 삼각형은 화면에서 여러개의 픽셀을 차지하고 있을 것
- fragment: 픽셀에서 사용할 색상 정보를 모아둔 것
fragment shader: 실제로 픽셀에 색상 정보를 대입(마지막 삼각형 모습)
Output merger: 색상 정보를 최종적으로 결정
위의 파란색 부분인 Shader는 프로그램과 같은 말로서 사용자가 직접 알고리즘을 제작해야 됩니다. 반면에 오렌지 색으로 표시된 rasterizer와 output merger는 하드웨어로 고정되어 있는 형태입니다.
Vertex shader

Vertex shader는 object space에서 clip space로 변환해주는 과정입니다. 이때 한번에 넘어가는 것이 아니라 world space와 camera space를 거쳐서 변환됩니다. 이전 4장에서 저희는 world transform(object → world space)를 배웠습니다.
World transform
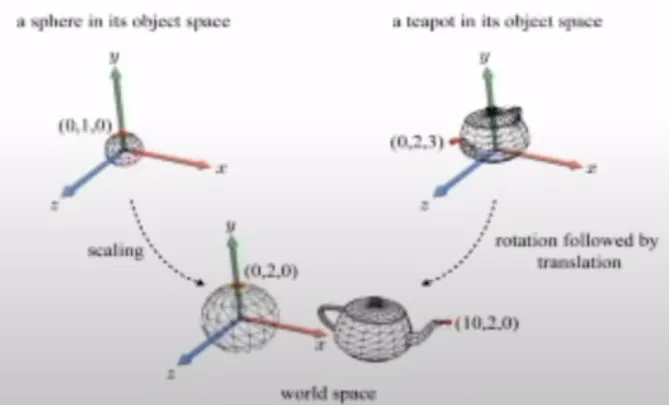
이 그림을 보면 어느정도 기억이 나실겁니다. 하지만 아직 완벽하게 world transform을 배우지 않았기 때문에 미흡한 부분을 집고 넘어가도록 하겠습니다.
이전에 world transform을 하나의 좌표 즉 vertex position에 대해서만 적용을 했는데, 그러면 다른 중요한 요소인 vertex normal에도 똑같이 적용할 수 있는지 확인해보도록 하겠습니다.
이전에 Scaling, Rotation, Translation과 같은 변환을 [L|t]와 같은 형태로 나타냈었습니다. 여기에 벡터 n을 곱해준다고 보면 Ln + t가 되는데 벡터에서의 덧셈은 무의미합니다. 왜냐면 벡터는 하나의 방향을 나타내고, t는 단순히 하나의 점이기때문에 덧셈을 할 수 없습니다. 따라서 vertex normal에서 Translation은 무의미합니다.
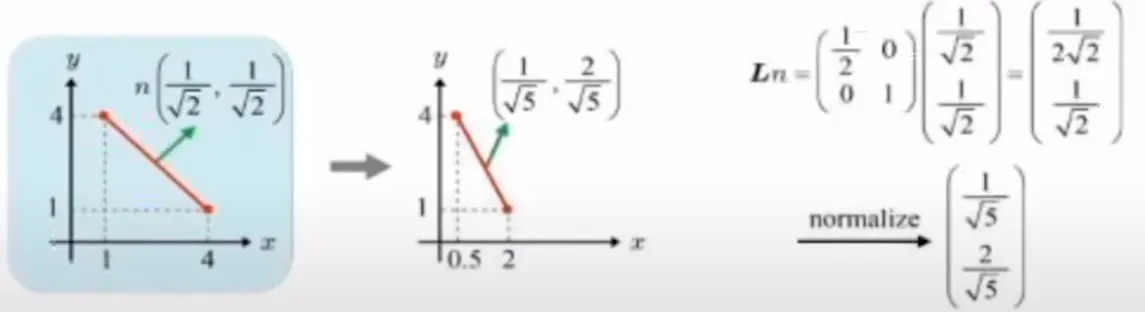
맨왼쪽에 표시된 선은 삼각형 중에서 xy평면과의 접선을 나타냅니다. 이때 삼각형을 non-uniform하게 scaling 했을 때 normal의 변화를 확인해보도록 하겠습니다. 맨 오른쪽에 보이는 것처럼 x축으로만 반 줄인다고 했을 때 x축의 값 4가 2로 변환되어서 오른쪽 빨간선으로 변할 것입니다. Normal은 scale요소중 L만 벡터 n에 곱한 다음 단위 벡터로 만들기 위해서 normalize 해주면 맨오른쪽 아래의 값이 나올 것입니다. Normal vector는 기울기가 2인 초록색 화살표인데 육안으로 봐도 직각이 아닙니다. 따라서 변환이 non-uniform일 때는 단순히 L을 n벡터에 곱하게 되면 오류가 발생합니다.
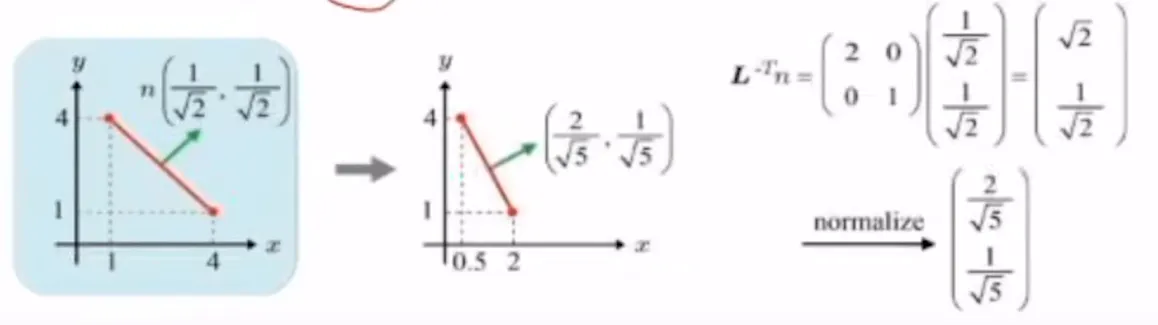
따라서 non-uniform일 때는 L을 곱해주는게 아니라 을 곱해줘야 됩니다. 기울기가 1/2인 normal vector를 오류 없이 구할 수 있는 것을 확인할 수 있습니다.
기본적으로 uniform일 때는 L을 곱하나 을 곱하나 결과가 동일하기 때문에, 그냥 통일해서 normal vector를 구할 때는 를 구하자고 정의했습니다.
View Transform
World space에서 카메라의 위치를 정의하는 방법에 대해서 설명해드리도록 하겠습니다.
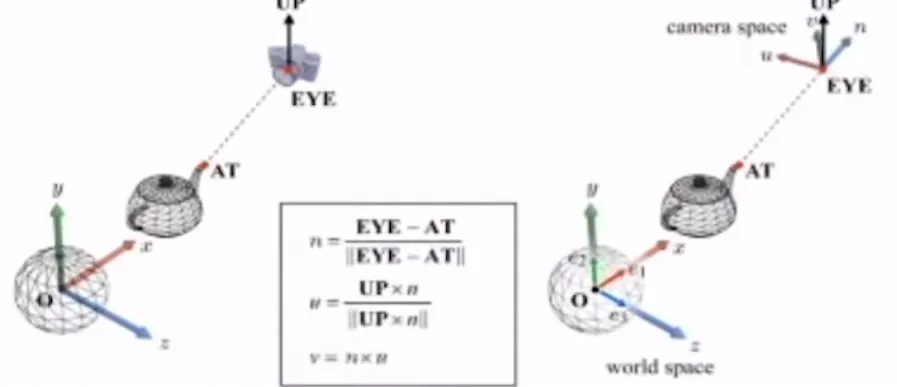
Eye: Camera position
AT: 카메라가 향하는 상대적인 위치 (카메라가 바라보는 방향, look AT)
UP: 카메라의 수직인 방향(카메라가 기울어졌을 때를 반영하기 위한 요소)
수식적으로는 AT에서부터 Eye까지 향하는 단위 벡터 n을 구합니다. 다음으로 Up과 n을 외적을 통해서 단위 벡터 u를 얻습니다. 마지막으로 n하고 u의 외적을 한번 더해서 v를 구하게 됩니다. n,u,v는 서로 수직이고 단위 벡터 즉 orthonomal 하게 됩니다.
만약에 EYE를 하나의 원점으로 둔다면 u,v,n은 EYE를 기준으로 한 basis가 될 것입니다. 따라서 {u,v,n,EYE}이 camera space를 정의하는 요소들입니다.
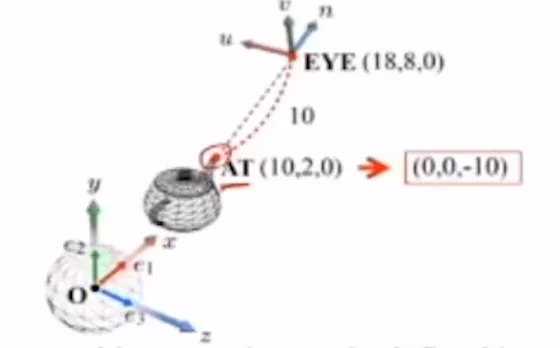
위의 예시를 통해서 구체적인 설명을 해보도록 하겠습니다. World space상에서 (10,2,0)의 좌표를 갖고 있는 점은 Camera space상에서는 (0,0,-10)을 갖게 될 것입니다. 즉 다른 좌표계에서는 다른 값을 갖게 될 것입니다. 수식적으로 구하는 방법은 AT이 EYE(Camera space의 원점)에 대해서 n방향의 값만 다르고 나머지 u와 v에 대해서는 변화가 없기때문에 u와 v좌표는 0입니다. 이후 원점에서 AT까지의 거리는 10이고 여기서 방향이 음수이기때문에 마이너스를 붙여주면 (0,0,-10)을 얻게 됩니다.
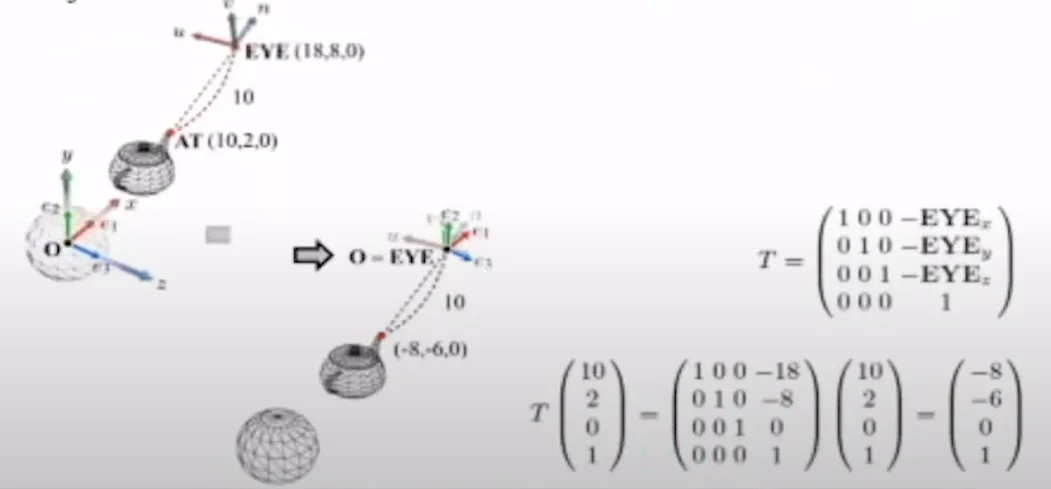
지금까지 하나의 점에 대해서 World space 에서 Camera sapce 로의 변환을 다뤄봤는데 이를 일반화 하는 과정을 진행해보도록 하겠습니다.
맨처음에 원점을 일치시켜야합니다. 그러려면 EYE를 원점 O로 이동시키는 translation 과정이 필요합니다. 따라서 맨오른쪽 위에 보이는 것처럼 EYE의 좌표를 4번째 열에 박아두면 됩니다.
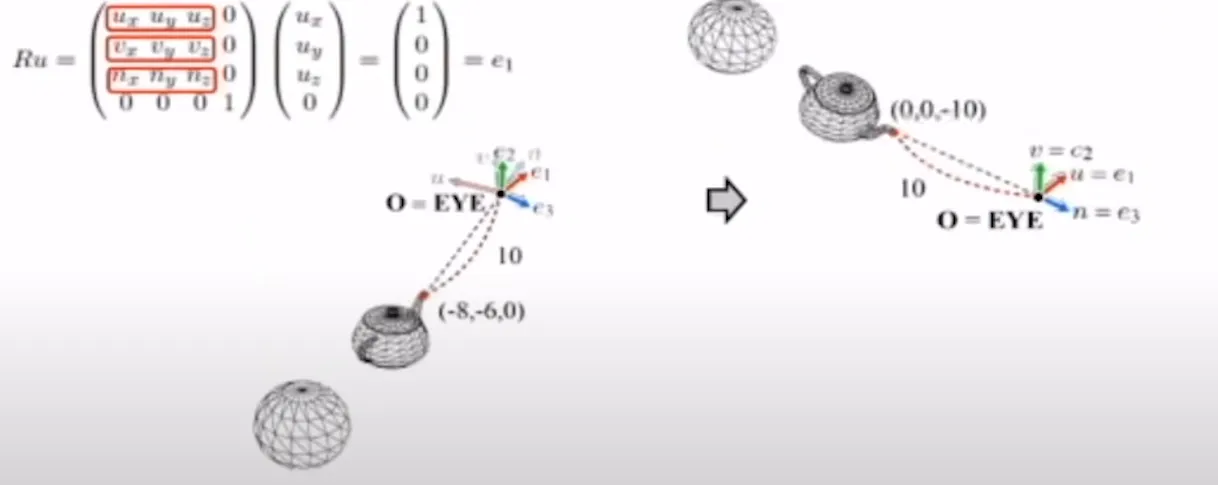
이제 왼쪽에서 오른쪽처럼 u,v,n을 회전시켜서 world space상에서의 와 일치되게 하면 두 좌표계가 동일하게 됩니다. 그러면 시작과 끝을 아는데 Rotation matrix를 모를 때 우리는 4장 마지막에서 transpose만 하면 해당 matrix를 얻을 수 있는 것을 알 수 있습니다. 따라서 u,v,n을 행으로 왼쪽 위에처럼 박아두면 그냥 바로 Rotation matrix가 됩니다(Transpose를 진행하니까).
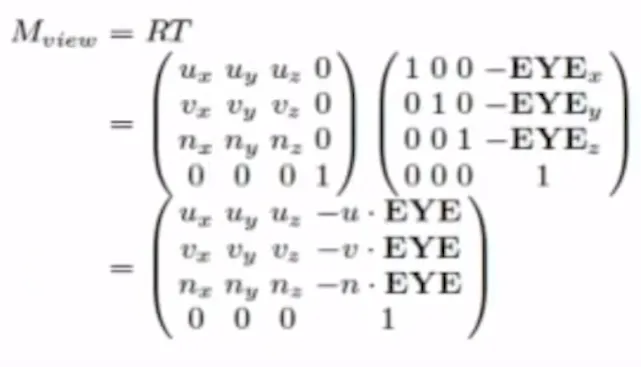
따라서 View transform은 translation 한 후 Rotation을 하게 되면 쉽게 얻을 수 있습니다.
Right-hand system vs Left-hand system
대부분의 방법이 오른손 좌표계를 사용하지만, 종종 왼손 좌표계를 사용하는 경우도 있기 때문에 왼손 좌표계에 대해서도 배워둬야합니다.
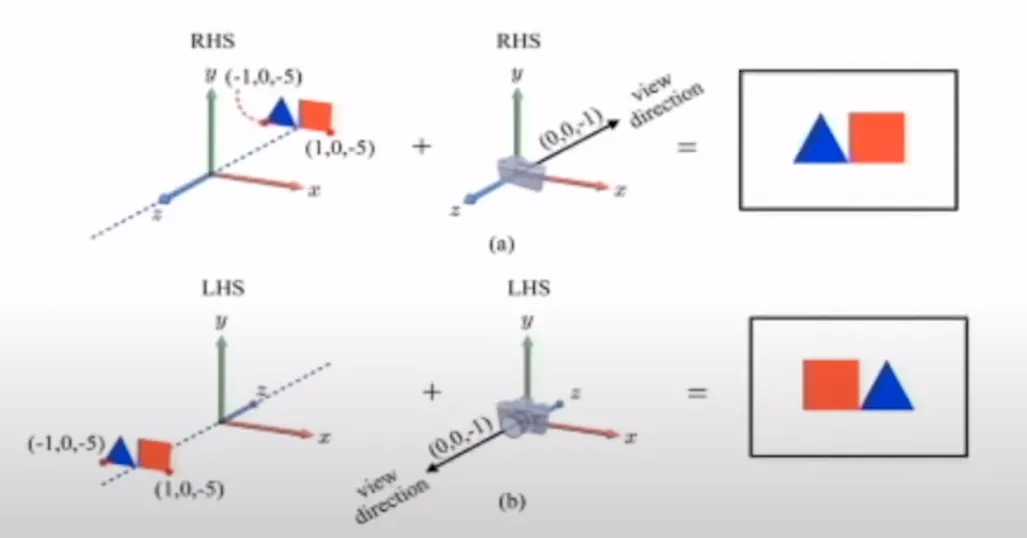
위의 예시에서 오른손 좌표계에서 계산을 통해서 카메라의 시점을 생각해보면 삼각형이 왼쪽이고 사각형이 오른쪽인 이미지가 나온다는 것을 쉽게 알 수 있습니다. 하지만 왼손 좌표계에서 동일하게 계산을 하면 사각형이 왼쪽이고 삼각형이 오른쪽인 결과가 나타납니다. 이처럼 동일한 좌표 값을 줘도 서로 다른 결과가 나타나게 됩니다.
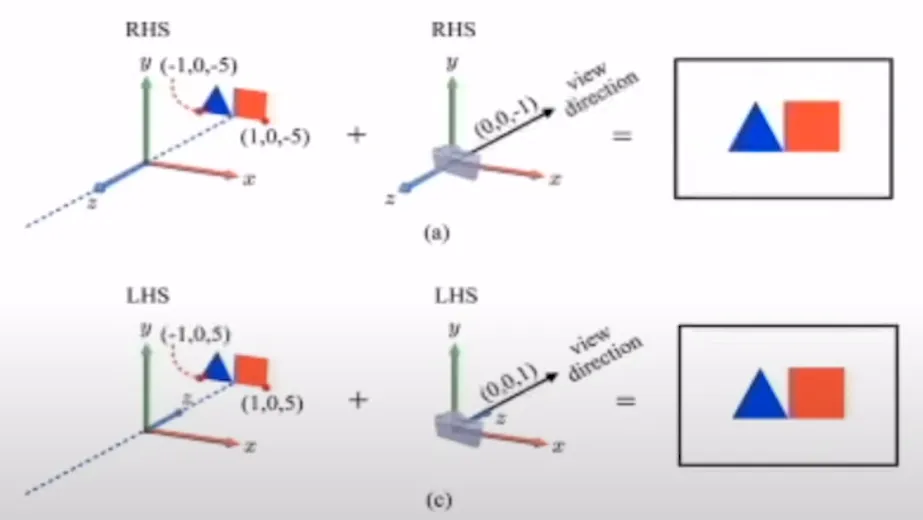
해결책은 간단합니다. z좌표의 부호만 바꿔주면 동일한 값을 얻을 수 있습니다.
View Frustum

지금까지 Camera space로의 변환을 알아봤는데 조금 더 자세히 알아보기 위해 실린더를 추가했고, Camera space에 대해서만 언급할거기 때문에 {uv,n}을 우리에게 익숙한 {x,y,z}로 표기하도록 하겠습니다.
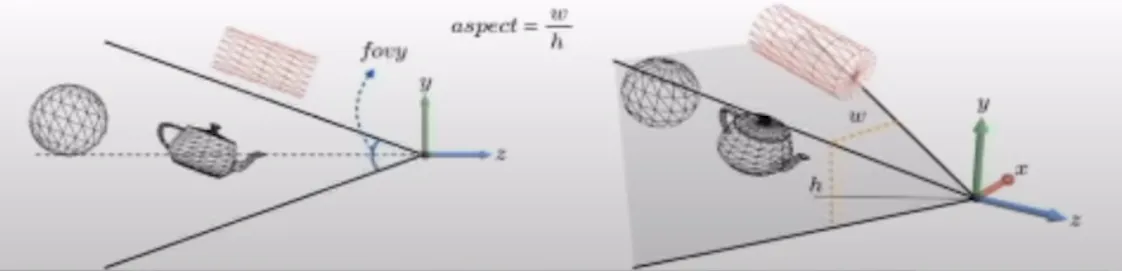
EYE, AT, UP과 같은 요소들은 카메라의 외부적인 요소들을 결정하는 external parameters라고 하고, 이제 internal parameters에 대해서 알아보도록 하겠습니다.
Field of view(fovy): y축 방향으로의 시야각
aspect: w/h의 값을 나타냄으로서 이를 통해서 무한한 피라미드 모양을 위의 그림처럼 나타낼 수 있다.
여기서 주목할전이 빨간색 실린더인데, 지금 피라미드 밖 즉 우리의 시야 밖에 보이기 때문에 카메라에 담지 않을 것입니다.
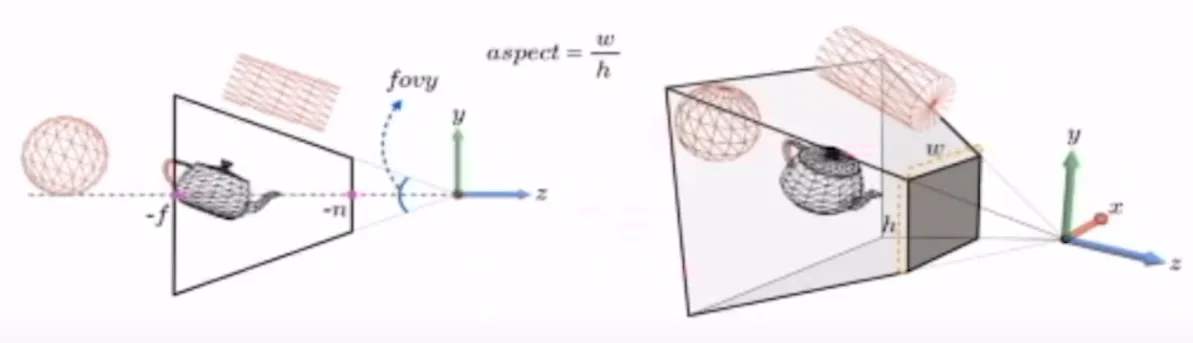
또한 우리의 시야에 무수히 많은 물체들이 존재할 수 있기 때문에 우리가 보는 부분을 제한해주는 요소들을 n과 f로 정의합니다. 즉 n과 f사이에 있는 물체만 보고 나머지는 보지 않겠다는 뜻 입니다. 이러한 피라미드를 truncated pyramid라고 하고 이를 view frustrum 이라고 정의합니다.
Projection transform
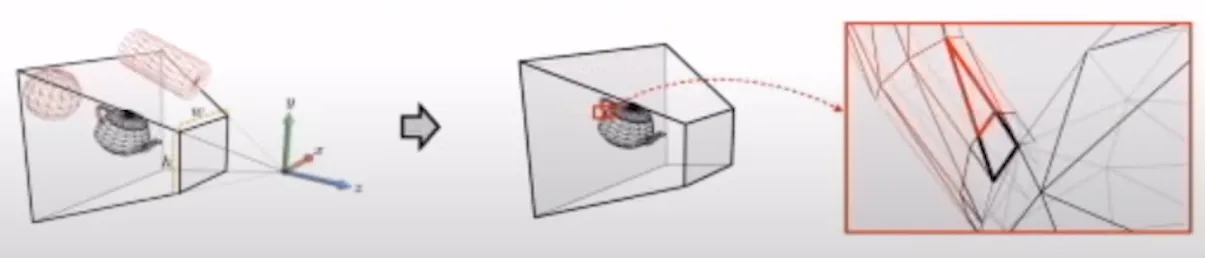
빨간색 물체들은 view-frustum 밖에 존재하기 때문에 제거하는데, 이 과정을 view-frustum culling이라고 합니다. 오른쪽에 보이는 것처럼 주전자 중에서도 view-frustum 밖으로 일부 빠져나갈 수 있는 경우가 나타납니다. 이렇게 밖으로 빠져나간 부분을 자르는 것을 clipped라고 정의합니다. 하지만 기울어진 면 4개를 기준으로 주전자를 짜르는 건 쉽지 않을 것입니다.
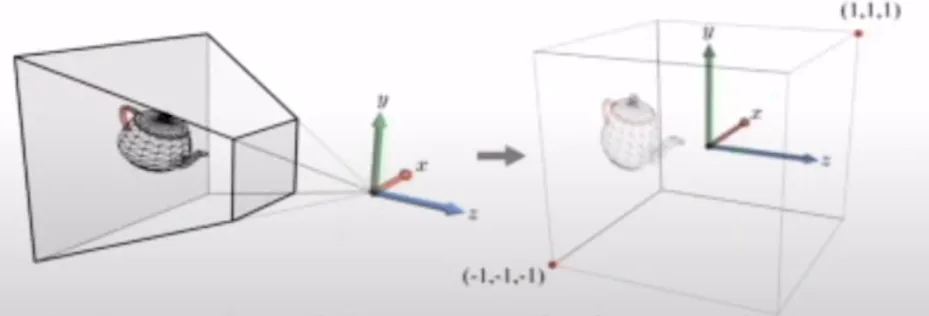
따라서 짜르기 쉬운 형태로 변환하는 과정이 필요합니다. 이렇게 짜르기 쉽게 변환하는 과정을 projection transform이라고 합니다. Projection transform 과정에서 주전자의 모양이 바뀌기 때문에 공간이 바껴야하고, 이렇게 새롭게 정의되는 공간을 clip space라고 부릅니다.
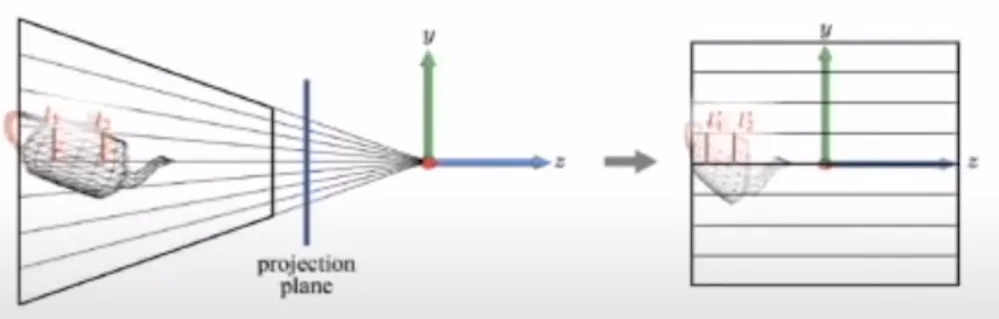
빨간색 점이 렌즈라고 했을 때 모든 빛이 모두 모여서 반대 방향으로 투영한다면, 주전자가 뒤집힌 형태가 나올 것입니다. 이러한 뒤집힌 현상을 방지하기 위해서 projection plance을 둡니다. 비스듬한 사각형을 반듯한 사각형으로 변환할 때 기존의 주전자에서 빨간색 선 l1과 l2가 어떻게 변할지 생각해봅시다. 왼쪽에서는 길이가 달랐지만 오른쪽에서는 길이가 동일한 것을 직관적으로 알 수 있습니다. 왼쪽에서는 뒤로 갈수록 길이가 길어지는 원근법 때문에 l1이 l2보다 길었지만, projection transform은 해당 효과를 누리지 못 합니다.
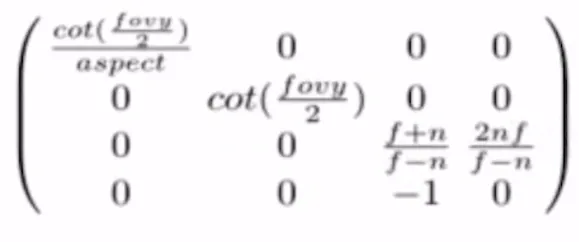
Projection transform은 위와 같이 정의되지만, 설명하면 길기 때문에 설명해주셨습니다. 어쨌든 우리가 알고있는 정보를 기반으로 이를 나타낼 수 있습니다.

이제 Vertex shader에서 모든 변환 과정을 배우게 됐습니다.
Rasterizer가 받아들이는 공간은 clip space이긴 하지만, 왼손 좌표계를 기준으로 받아들입니다. Rasterizer는 하드웨어 영역이기 때문에 vertex shader에서 변환해줘야 합니다. 따라서 vertex shader에서 왼손 좌표계로 변환해서 rasterizer에게 보내줘야 합니다.
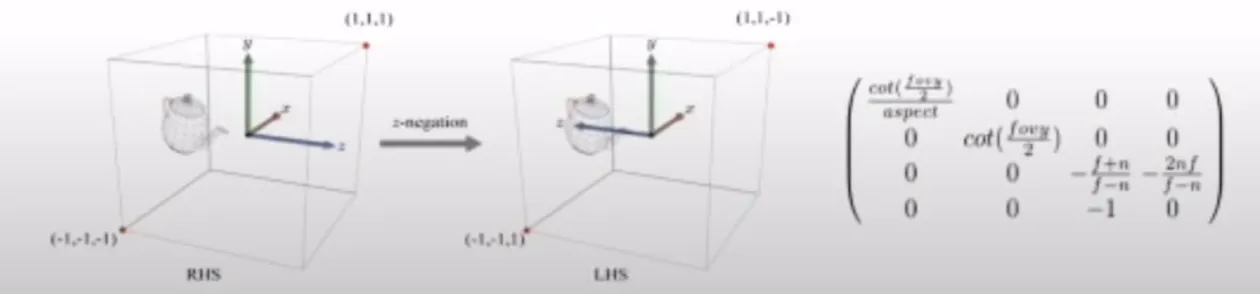
왼손 좌표계로 변환하기 위해서는 위에서 배운 z좌표계에 음수만 붙이면 됩니다. z의 값에 영향을 주는건 3번째 행밖에 없기때문에 3번째 행을 음수로 바꾸면 왼손 좌표계를 한번에 얻을 수 있습니다.
