출처: https://www.youtube.com/watch?v=CAfdIW8M6HA&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=6
한정현님의 컴퓨터그래픽스 7장 강의를 기반으로 제작한 블로그입니다.Rasterizer
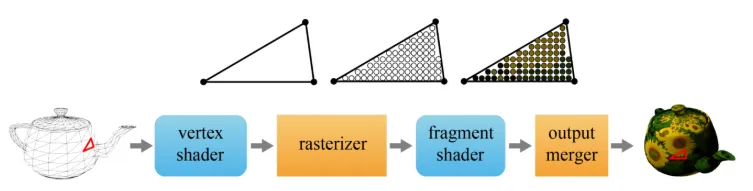
5장의 강의에서 Vertex Shader의 마지막 출력값이 clip space에서의 결과였습니다. 따라서 해당 값으로 rasterizer는 clip space의 점들을 삼각형으로 만들고(맨 왼쪽), 이를 여러개의 fragments(가운데 그림)으로 나누는 과정을 진행합니다.
Clipping
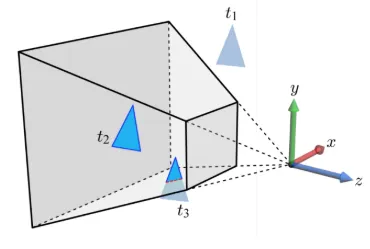
Clipping은 clip space상에서 수행되지만, 설명을 위해서 camera space상에서의 그림을 나타냈습니다. 큰 개념은 5장과 같습니다. View-frustrum 안쪽의 삼각형만 유효하기 때문에 은 제거됩니다. 이때 의 같은 경우 일부만 안쪽에 존재해서, 안쪽 부분을 기준으로 새로운 삼각형을 생성하게 됩니다.
왜 vertex shader에서도 clipping을 진행하는데, rasterizer에서도 진행할까?
수업 시간에 설명은 없었지만, vertex shader에서는 삼각형 단위로, rasterizer에서는 픽셀 단위로 서로다른 단위를 통해서 정교하게 진행된다고 구글링을 통해서 알아냈습니다.
Perspective Division
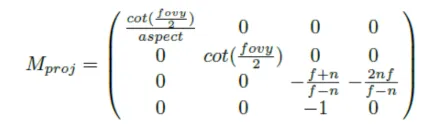
5장의 마지막 부분에 나온 projection transform 행렬입니다. 위의 행렬을 자세히 설명하진 않았지만, 4번째 행을 보시면 기존에 [0,0,0,1]과는 다른 [0,0,-1,0]인 것을 확인할 수 있습니다.
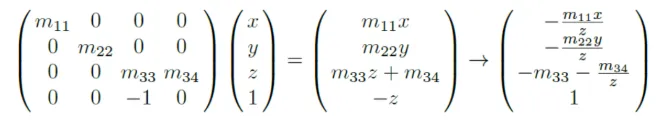
따라서 각 원소들을 m으로 치환했을 때 4번째 행의 결과가 1이 아니라 -z가 나옵니다. 1로 변환하기 위해서 나머지 행들에도 똑같이 -z를 나눠주면 이전과 동일하게 x,y,z로 나타낼 수 있습니다. 그러면 -z로 나눠준다는게 어떤 의미가 있는지 확인해보도록 하겠습니다.

Projection transform의 행렬을 정확히 구하기 위해서는 위의 4가지 변수를 알아야합니다.
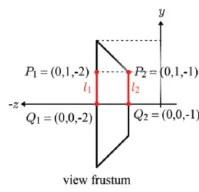
이 그림을 기준으로 4개의 변수를 설명해드리겠습니다. 첫번째로 fovy는 시야각으로 원점에서 까지 45도이고 이를 -z축으로 대칭하면 90도 이니까 /2 라는 것을 알 수 있습니다. 두번째로 aspect는 frustum의 가로 세로 비율인데, 사다리꼴에서 기울기가 1이니까 비율이 1이라는 것을 쉽게 확인할 수 있습니다. n=1인 것은 와 의 z좌표가 -1이니까 원점으로부터 거리가 1, 마찬가지로 f=2인 것은 과 의 원점으로부터 거리가 2인 것입니다.
이렇게 4가지 값을 행렬에 대입하면 오른쪽과 같이 간단한 수식을 얻을 수 있습니다.
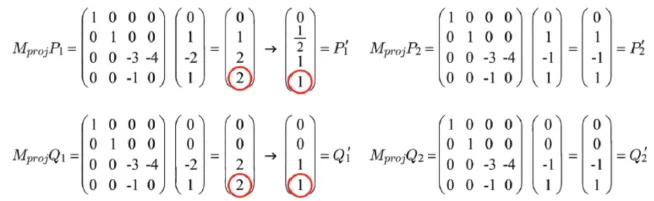
4개의 좌표에 각각 행렬을 적용해서 새로운 4개의 점을 얻은 결과입니다.
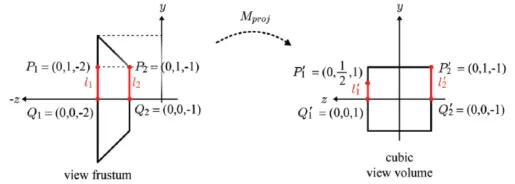
이를 시각화 하면 위와 같습니다. View frustum이 원근감을 주기 위한 방법이라고 5장에서 배웠을 텐데요, 원점에서 멀리 있는 은 거리가 줄고, 는 거리가 안 준 것을 확인할 수 있습니다. 여기서 거리가 준 만큼은 4번째 행의 값(2,1)인데 이 값이 바로 -z인 것입니다.
따라서 -z는 원점에서 얼마나 떨어져있고, 해당 값의 역수값에 비례해서 길이가 줄어든다는 것을 의미합니다.
추가적으로 마지막 결과를 보면 x,y,z좌표가 모두 1이내에 존재하는데, 이를 NDC(normalized device coordinates)라고 합니다.
Back-face Culling
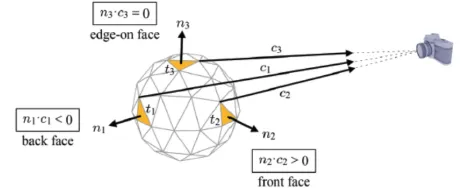
3번째 Culling 내용입니다. 기존에는 view-frustum을 기준으로 안보이는 부분들을 제거했다면, 이번에는 카메라가 안보이는 면들을 내적 값을 기준으로 제거합니다
첫번째 삼각형 의 normal인 와 삼각형에서의 한점과 카메라를 잇는 의 내적값은 수직이기 때문에 0입니다. 이때가 카메라가 보이는 마지노선으로 edge-on face라고 하고, 0보다 큰 범위는 다 보이는 front face, 작으면 다 안 보이는 back face입니다.
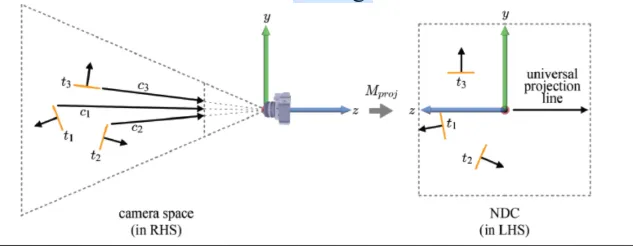
x축을 제거하고 yz평면으로 나타내면 위와 같습니다. Camera space에서 perspective division을 거치면 오른쪽과 같은 NDC의 형태가 되는데, 이때 모든 선들이 평평해지고 x,y,z 값이 1이내에 나타나게 됩니다. NDC에서의 내적을 통해서 제거할 면들을 정할 수 있지만 더 간단한 형태로 back face를 제거하는 방법을 알아보겠습니다.
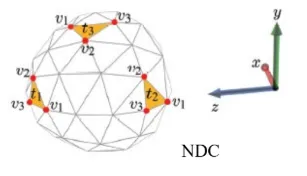
이전에 봤던 구와 달리 위에 보이는 구는 원근법이 적용됐기 때문에 약간 찌그러진 것을 확인할 수 있습니다. 이 Culling 된 구에 대해서 z축은 무시하고 x,y 좌표값만 고려해보도록 하겠습니다.
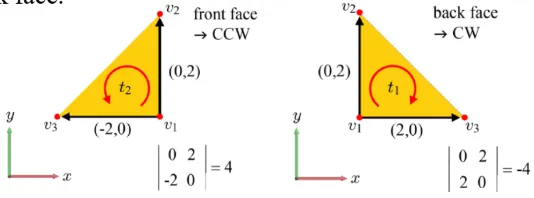
눈이 구의 오른쪽에 있을 때 이 오른쪽, 는 왼쪽 마지막으로 는 위쪽에 있는 것을 알 수 있습니다. 이를 그렸을 때 왼쪽과 같이 반시계 방향으로 이전에 배웠던 것처럼 잘 나타났습니다. 하지만 반대편에 존재하는 삼각형인 에 대해서 그리면 시계 방향입니다. 당연히 구가 반바퀴 돌았기 때문에 좌우 반전된 형태일 것입니다.
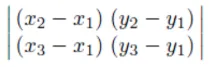
삼각형의 x,y 값에 대해 {v1-v2}와 {v3-v1}의 벡터의 행렬값을 구하고, 부호가 양수라면(왼쪽의 경우) front face, 음수라면(오른쪽의 경우) back face입니다.
무조건 back face를 날려야할까?
→ 반투명한 구라면 back face를 날리면 안되고(Disable), 구의 단면을 보고싶다면 front face를 날려야 합니다. 따라서 이를 파라미터로 설정하도록 설계 되어있습니다.
실제 사용 사례
Sync MVD: 3D Model을 UV map으로 변환해주는 Backprojection시 겹치는 부분에서 어떤 부분에 가중치를 줄까? → normal vector와 view direction 간의 코사인 유사도 계산
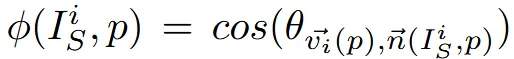
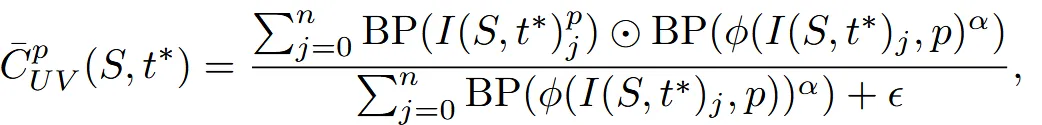
Viewport
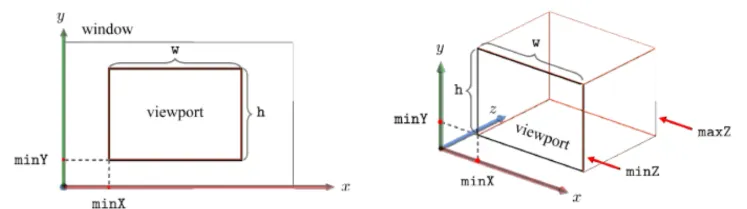
실제 Window 안에서 우리가 그림을 그릴 영역을 viewport라고 합니다. xy평면 전체를 그릴 수도 있고, 아니면 4등분 해서 어디는 front, 어디는 back 구역별로 다르게 정의할 수 있기 때문에 이를 명시해줘야 합니다.
왼쪽과 같이 시각적으로 viewport는 2차원 같지만, 실제로는 z차원도 고려하는 3차원 입니다. 그리고 주의해야 할 점은 3차원 좌표계는 왼손 좌표계 기준입니다.
Vertex shader에서 지금까지 Object Space(World Transform) → World Space(View Transform) → Camera Space(Projection Transform) → Clip space(Viewport transform) → Screen Space 이렇게 나타낼 수 있습니다. 마지막에 나타난 viewport 관련 부분을 방금 설명해드린 것입니다.
Viewport Transform
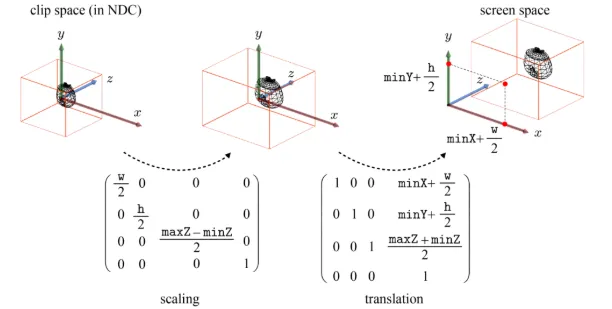
이제 Viewport Transform의 행렬이 어떻게 나타나는지 확인해보도록 하겠습니다. 최종적으로 우리가 원하는 형태는 정육면체가 아닌 직육면체로 screen space를 정의했습니다. 이에 맞게 수정하기 위해서 원래 정육면체에서 모든 변의 길이가 2인 부분을, 가로 w, 높이 h, 세로 maxZ - minZ로 바꿔야 겠죠? 이렇게 길이를 맞추는 과정이 왼쪽의 행렬인 scaling입니다. 그리고 주전자가 원점에 있었던 것을 맞춰주기 위해서 다시 translation(오른쪽의 행렬)을 진행하게 되는 것입니다.
Scan Conversion
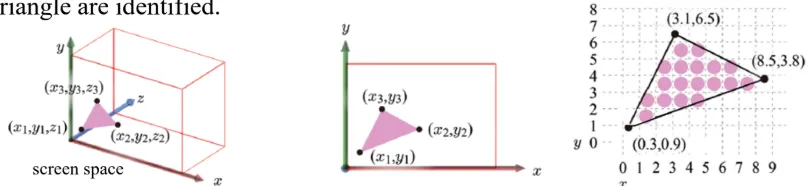
첫번째 사진의 Screen space(3차원)을 xy평면(2차원)으로 나타내면 두번째 그림이 될 것입니다. 두번째 그림의 삼각형 세 꼭짓점 안에는 오른쪽과 같이 많은 픽셀들이 존재할 것입니다. 하나의 픽셀에는 x,y,z 좌표뿐만아니라 normal이나 texture와 같은 정보들도 존재하기 때문에 이를 구해줘야 하고, 이 과정이 scan conversion입니다.
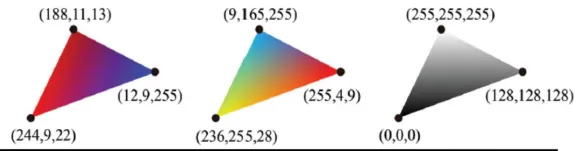
삼각형의 각 꼭짓점에 대해서는 normal과 texture 혹은 색상 정보를 알기 때문에 이를 이용해서 interpolation을 적용하면 각 픽셀에서의 값도 얻을 수 있습니다. 예를들어서 맨 오른쪽 사진에서 윗 부분이 흰색, 맨왼쪽 아래가 검은색일 경우 그 사이 값들은 회색처럼 중간값을 갖게 될 것입니다.
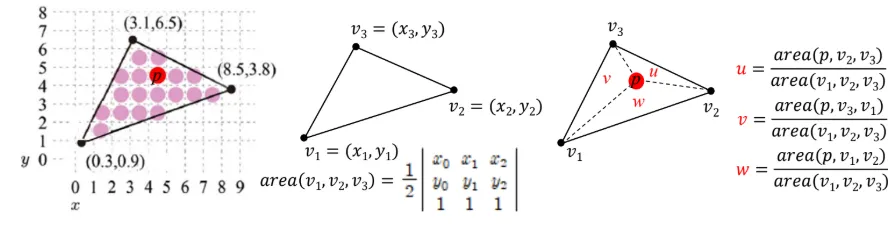
우리가 픽셀 p에서의 interpolation된 값을 얻기 위해서 interpolation을 해야된다고 위에서 말씀드렸죠? Interpolation 방법을 유튜브 강의에서는 기울기를 통해서 직접 얻는 과정을 나타냈고, 강의록에서는 넓이로 위와 같이 구하는 방법을 나타냈습니다. 같은 방법인데 강의록 기준으로 설명드리자면 우리는 삼각형의 넓이를 행렬식을 통해서 얻을 수 있습니다. 삼각형을 v,u,w로 나누고 각각의 작은 삼각형의 넓이 역시 p좌표가 구해진 상태에서 다시 행렬식을 통해서 얻으면 넓이의 비율도 나오게 됩니다.
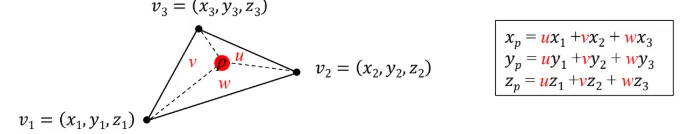
이 넓이의 비율을 이용해서 p좌표의 normal이나 texture 정보를 각 점의 가중치를 통해서 위와 같이 얻을 수 있습니다.

p의 위치가 바뀌면 u,v,w값들이 바뀌겠지만, 항상 합은 1이여야 합니다.
