출처: https://www.youtube.com/watch?v=CAfdIW8M6HA&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=6
한정현님의 컴퓨터그래픽스 9장 강의를 기반으로 제작한 블로그입니다.
Lighting
Lighting과 illumination은 light와 object간의 상관관계를 다루는 기술입니다. 두가지 기술을 이용해서 더 자연스러운 표현이 가능해지게 됩니다.

실제로 texture만 입힌 왼쪽 사진보다 lighthing까지 적용한 오른쪽 사진이 더 사실적인 표현이 가능한 것을 확인할 수 있습니다.
illumination은 크게 global illumination과 local illumination으로 나눠지는데, 9장에서는 local illumination에 관련된 Phong lighting 부분만 먼저 살펴보도록 하겠습니다.
Phong Lighting Model
Diffuse Term

다양한 형태의 light(광원)이 존재하지만, 9장에서는 directional light source만 다루도록 하겠습니다. Directional light source는 태양과 같이 광원이 물체로부터 매우 멀리 떨어져있어서 모든 방향에서 빛이 동일하게 작용하는 것이고, 왼쪽과 같이 point light의 경우 방향에 따라서 빛의 영향이 달라져서 그림자가 다르게 형성됩니다.
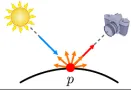
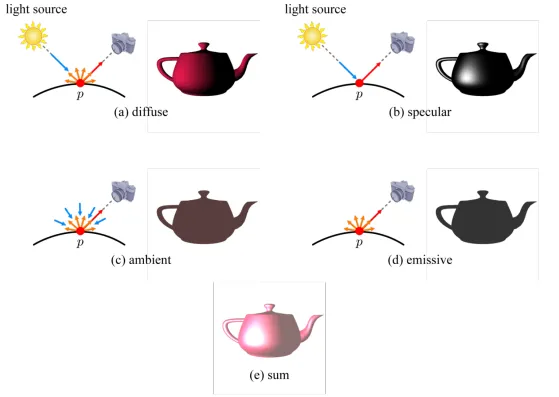
첫번째 다루는 부분은 Diffuse(난반사)로서 모든 방향에서 반사되는 빛의 양이 동일하게 됩니다. 위의 사진처럼 카메라의 위치가 어디에 있든 상관없이 빛(p)은 동일하게 관측될 것입니다.
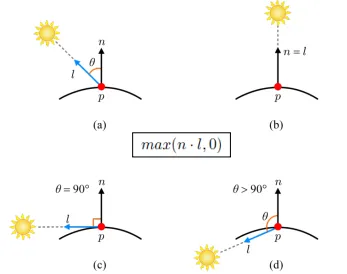
빛의 방향은 고려 대상이 아니기 때문에 빛의 세기를 고려해보도록 하겠습니다. 물체 p에서 광원까지의 light vector를 l이라고 하고, 물체의 normal vector를 n이라고 할 때 두 벡터의 내적의 결과가 빛의 세기입니다. 따라서 0도일 때 최대 90도일 때 최소입니다. 이를 함수로 나타내면 로 나타낼 수 있습니다. 이때 주의할 점은 90도 보다 커졌을 때 cos은 음수가 되기 때문에 max(n.l, 0)을 사용해서 최솟값은 0으로 두도록 합니다. 왜냐하면 광원이 음수의 영향을 주는건 없기 때문입니다. 참고로 n과 l의 크기를 1로 설정하면 내적의 값과 cos의 결과는 동일합니다.
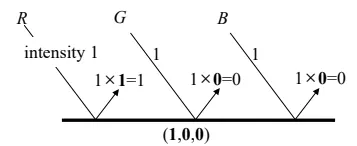
만약에 광원의 RGB값이 (1,1,1)이라고 했고, 반사 계수의 RGB가 (1,0,0)이라고 했을 때 우리는 위와 같이 빨간색 빛만 반사되는 것을 알 수 있습니다.
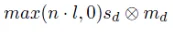
따라서 diffuse term의 최종 수식은 위와 같습니다. 이전에 배운 내적값(cos)을 통해서 빛의 세기를 정하고, 광원과 반사계수의 원소 곱을 통해서 나타냅니다.
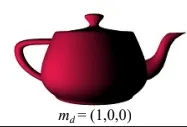
예시 그림입니다. 반사계수를 통해서 Red 값만을 나타내는데, 어떤 부분은 내적값이 작아서 검정색에 가까운 값을, 어떤 부분은 내적값이 커서 빨간색을 나타내는 것을 알 수 있습니다.
Specular Term
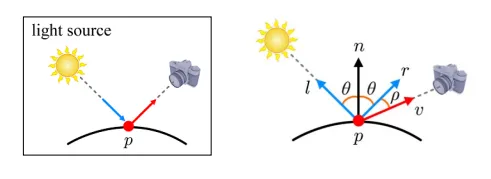
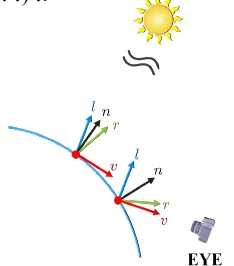
이전에 배운 Diffuse(난반사)와 다르게 Specular(정반사)는 빛의 방향이 일정한 것을 말합니다. 이때 반사되는 빛의 벡터를 reflection vector(r)로 표현합니다. Reflection vector는 normal vector에 대해서 light vector와 정확히 대칭을 이루게 됩니다. 그리고 이전에는 카메라의 위치에 따라서 빛의 변하지 않았지만, specular의 경우 카메라 시점 view vector(v)에 따라서 빛이 변하게 됩니다.
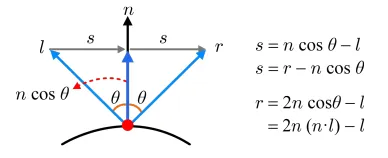
Relfection vector를 계산하기 위해서 필요한 요소들만 위의 사진에서 가져왔습니다. 우선 s벡터를 n과 l에 대한 수식으로 나타내고, n과 l의 크기가 1이므로 내적은 코사인과 같은 결과를 야기하기 때문에 최종적으로 r을 n과 l에대한 수식으로 나타낼 수 있습니다.
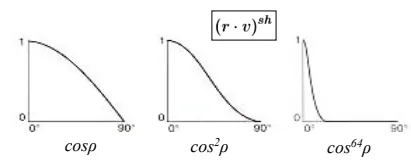
그러면 refleciton vector롸 view vector간의 각도를 ρ라고 했을 때 ρ가 커질수록 더 적은 빛을 보는건 알겠는데 그 비율은 어느정도일까요? 처음으로 cos함수를 생각할 수 있지만 cos60이 1/2을 갖기 때문에 실제로 조금만 벗어나도 보이지 않는 정반사에 적합하지 않는 함수입니다. 그래서 제곱을 해봤지만 만족스럽지 않았고, 더 많은 지수승을 실행하게 된 것입니다. 실제로 지수를 결정하는 요인은 sh(shiniess)입니다. 물체가 거울처럼 매끈할수록 sh 값은 커지게 됩니다.
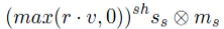
최종적으로 빛의 세기와 음수를 갖지않도록 고려한 specular 식은 위와 같습니다.
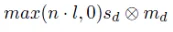
이전 diffuse 수식과 비교해보면 s와 m의 아래첨자가 s와 d로 다른 것을 확인할 수 있습니다. 실제로 물체 고유의 색인 와 는 동일하고, 는 rgb에 대한 빛의 반사, 는 gray scale에 대한 빛의 반사를 나타냅니다. 이렇게 다르게 설정한 이유는 sepcular의 경우 물체 고유의 색은 줄이고 원래 license의 색은 그대로 내보내줍니다. 따라서 빛을 얼마나 보내줄지를 결정하기 위해서 rgb대신 gray scale을 선택한 것입니다.

실제 예시 그림입니다. 흰색 부분은 r과 v의 각도가 작아서 하얗게 보이고, 검은색 부분들은 r과 v의 각도가 클 것이라고 추정할 수 있습니다.
Ambient and Emissive Terms

빛이 존재하지 않을 때도 물체가 어느정도 형태가 보이는 경우가 있었을 것입니다. 그 경우가 바로 Ambient입니다. Ambient는 온갖 방향에서 빛이 들어고, 이에 따라 반사되는 빛도 온갖 방향으로 나가게 됩니다. 따라서 계산을 할때도 벡터나 각도가 영향을 주지않고, 단순히 맨 오른쪽 수식처럼 나타낼 수 있습니다.
마지막으로 스스로 빛을 내는 Emissive는 그냥 원소의 곱 필요없이 로 나타낼 수 있습니다.
Phong lighting model
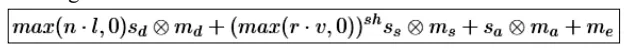
최종적으로 4가지 요소를 모두 더한 값이 Phong Lighting model입니다.
시각적으로는 위와 같이 4개의 색을 합쳐서 맨 아래의 결과가 나오게 됩니다.
Pre-fragment Lighting
이제 그러면 각 fragment 별로 어떻게 lighting을 계산하는지 알아보도록 하겠습니다. 우리는 directional light를 사용하기 때문에 l은 uniform한 값입니다. n과 v는 fragment마다 다르기 때문에 n과 v는 rasetrizer가 계산해줄 것입니다. 마지막으로 r은 n과 l을 통해서 자동 계산 됩니다.
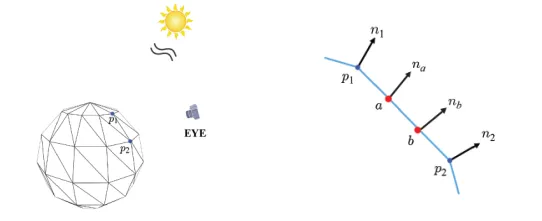
여기서 주의해야될게 우리가 처음 입력으로 받은 object에 대한 normal vector는 object space상에 정의되어 있고, directional light는 world space상에서 동일하게 적용될 것입니다. 즉 두 벡터의 space가 다르기 때문에 이를 world space로 통일 시켜줘야 합니다. Rasterizer는 하드웨어 이기 때문에 이 과정은 vertex shader에서 진행하고 rasterizer로 넘어가야 합니다.
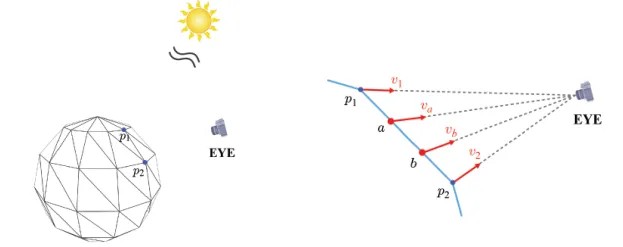
n 벡터를 world space로 보냈던 것처럼, 각 fragment와 카메라의 관계를 나타내는 v벡터도 object space에서 world space로 변환된 후 rasetizer로 넘어가야 합니다.
실제 사용사례
DIffusion-light

