출처: https://www.youtube.com/watch?v=CAfdIW8M6HA&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=6
한정현님의 컴퓨터그래픽스 8장 강의를 기반으로 제작한 블로그입니다.
요약
Image Texture

Image를 Mesh에 대입하는 image texturing이 대표적인 texturing 방법
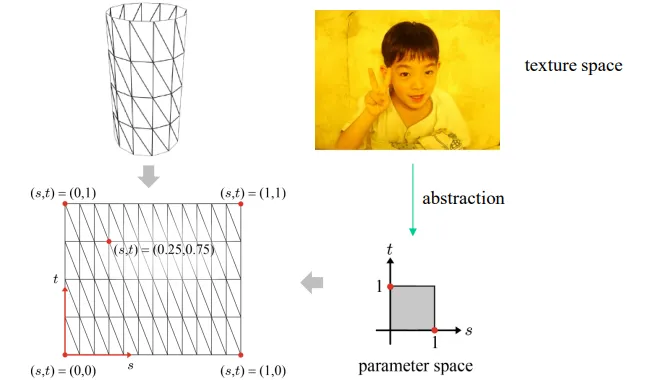
Image라는 2D 정보를 3D mesh에 대입하기 위해서는 아래와 같은 방법을 진행해야 됩니다.
Unfold : 3D Mesh를 2차원 UV space로 변환하는 과정
Parameterization : 3D Mesh의 표면을 2D 평면(UV Space)으로 변환하는 과정

chart/atlas 만들기 : 전체 mesh 중 일부분을 펼쳐서 얻은 uv map은 chart, 이를 전부 합친게 atlas
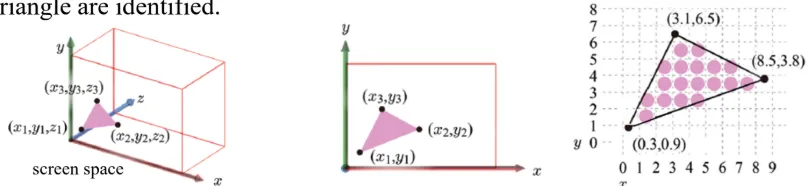
Scan conversion : 삼각형 꼭짓점 세점을 이용해서 삼각형 내부의 fragment의 normal, texture 값 얻기
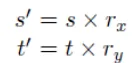
Projection : 2D 공간에서의 texture 좌표를 3D mesh에 매핑하는 과정. (s,t) → (s’,t’)
texturing : Atlas를 3D mesh에 매핑해주면서 texturing된 3d mesh 획득
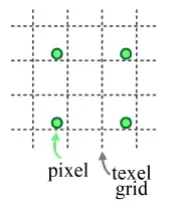
Texture Wrapping

반복되는 패턴을 표현하기 위해서 [0,1]의 범위를 벗어나는 값을 사용.
벗어나는 값을 사용하면 원래는 검정색이지만, texture Wrapping을 통해서 값을 갖도록 변경
Clamp-to-Edge : (c)그림을 보시면 1을 넘는 영역은 모두 1의 값을 갖도록 합니다.
Repeat: (d)의 그림을 보시면 타일들이 반복됩니다. 알고리즘은 1을 넘는 픽셀의 정수 값을 버리게 되어서 0~1의 값이 반복되게 됩니다.
Mirrored-Repeat: Repeat을 사용하면 경계 부분에서의 변화가 너무 뚜렷하게 보여서, 거울을 이용해서 texture를 대칭적으로 갖도록 하는 방식
Texture filling
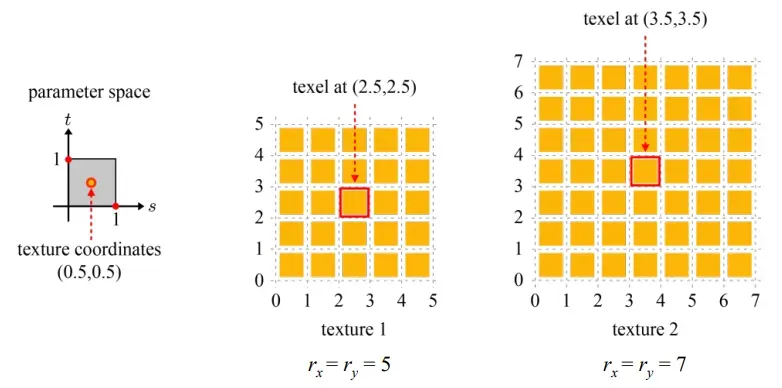
Projection시에 왼쪽과 같이 하나의 texel(texture의 픽셀)에 여러개의 fragment가 존재할 수도, 오른쪽과 같이 여러개의 texel에 하나의 fragment가 존재할 수도 있습니다. 따라서 texture filling(mangnification, minification)을 진행해야 합니다.
Magnification

Magnification은 texture의 크기가 작아서 texels에 여러개의 fragment가 존재하는 경우입니다. 이경우 2가지 방법으로 texture를 확대할 수 있습니다.
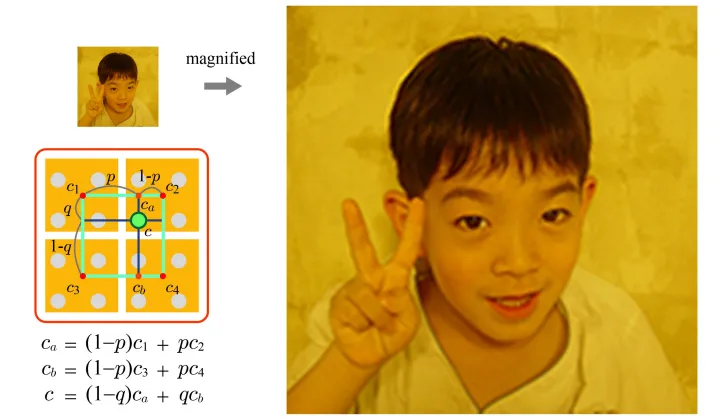
Nearest point sampling: 해당하는 texel값을 fragment가 갖기(왼쪽 그림)
Bilinear interpolation: fragment들이 texel의 bilinear interpolation을 통해서 계산
Minification : mipmap
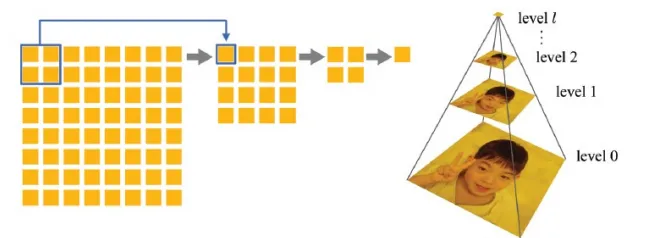
Minification은 texture의 크기가 커서 여러개의 texel에 1개의 fragment가 존재하는 경우입니다. 이 경우 mipmap을 사용해서 texture의 크기를 줄일 수 있습니다.
Mipmap은 큰 해상도의 texture map을 여러 작은 해상도의 texture map으로 변경해서 모두 저장하도록 하는 방식
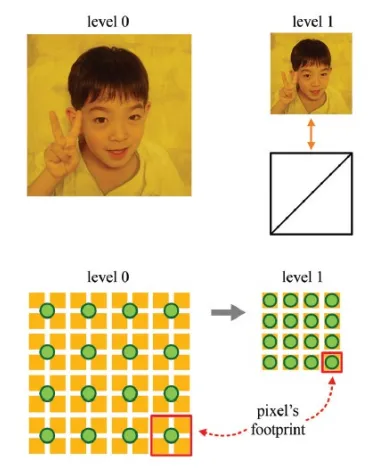
하나의 픽셀에 대응하는 값을 footprint(mxm)라고 하는데 해당 값만큼의 texel을 1개의 texel로 변환합니다. 의 레벨을 선택합니다.
의 값이 정수가 아닌 경우 upper, floor, triliner interpolation 중 하나를 이용해서 선택합니다. Triliner interpolation은 오른쪽과 같이 2가지 level에 대해서 interpolation을 한번 더 진행하는 것 입니다.
Texturing
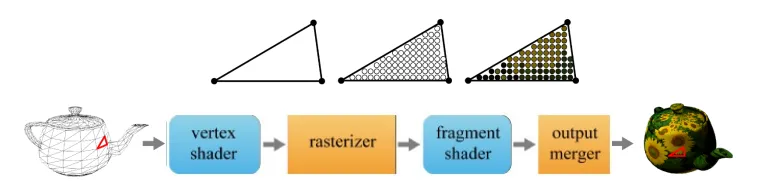
다시 한번 컴퓨터 그래픽스의 GPU pipeline을 확인해보도록 하겠습니다. 7장까지 우리는 rasterizer 부분을 배웠고, 해당 부분까지의 정보는 삼각형안에 fragment가 있고 각 fragment에는 normal과 texture가 정보가 존재한다는 것을 배웠습니다. 이제 마지막 삼각형처럼 색깔 정보를 주는 과정을 배워보도록 하겠습니다.
색깔 정보를 주기 위해서는 Lighting과 Texturing 정보가 필요합니다. 8장에서는 Texturing을 먼저 살펴보도록 하겠습니다.
Image Texturing

Texture를 표현하는 가장 쉬운 방법은 image texturing입니다. Image texturing은 이미지를 물체의 표면에 대응되게 붙이는 것을 말합니다.
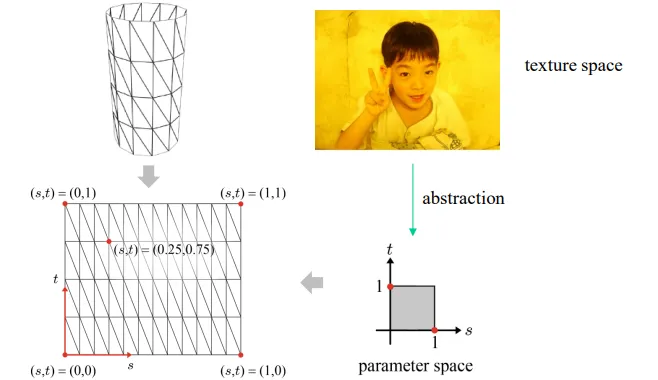
3차원의 mesh를 좌표로 표현하기 위해서는 2차원으로 펼친 좌표계로 변환을 하고, 이를 texture coordinates의 정보와 매핑해줘야 합니다.

Image를 물체의 표면에 붙일 때 기본적으로 2D 배열의 texels를 붙이게 됩니다. pixels라고 표현해도 되지만 이미 표현되는 방식과 혼란을 줄 수 있기 때문에 texels로 정의합니다.
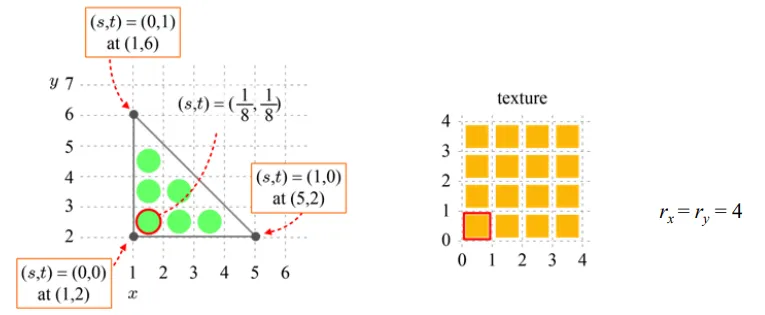
Texutre를 입히기 위해서는 modeling 단계에서 각 vertex마다 texture 좌표(s,t)가 정의되어 있어야 합니다.
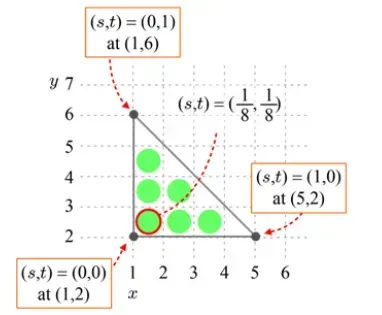
2개의 좌표를 매핑하기 위해서는 우선 s,t의 좌표를 구해야합니다. 우리가 삼각형 각 꼭짓점에서의 좌표를 알고 있기 때문에 이를 이용해서 픽셀의 좌표를 구해보도록 하겠습니다. 맨 왼쪽의 픽셀을 구한다고 했을 때 왼쪽 두 픽셀의 s값의 차이는 없고 t값의 차이는 1입니다. 높이는 4이기 때문에 한 칸당 1/4씩을 차지할 것이고 픽셀 값의 t좌표는 1/8일 것입니다. 마찬가지로 s좌표도 구하게 된다면 1/8이 나오게 됩니다.
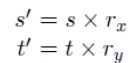
이렇게 구한 (s,t)의 좌표에 texture의 해상도를 이용해서 매핑되는 texels를 구합니다. Texutre의 높이와 너비가 모두 4이기 때문에 최종적으로 s’과 t’은 0.5이고 이 값은 맨 왼쪽의 빨간색친 texels 값입니다. 결과 적으로 빨간색 친 픽셀과 빨간색 친 texels가 매핑됩니다.

실제 예시를 통해서 지금까지 살핀 개념을 확인해보도록 하겠습니다. 3D mesh의 빨간색 삼각형 부분이 오른쪽의 texture image에서 눈쪽에 삼각형 빨간색으로 매핑 되는 것을 확인할 수 있습니다. 이때 이미지의 해상도는 640,480인데 이를 s’, t’을 구할 때 곱해주는 과정을 진행합니다. 즉 정규화된 좌표에 , 를 곱해줘서 매핑해주는 것입니다. 정규화된 좌표인 이유는 rasterizer과정에서 좌표가 정규화되기 때문입니다. 그리고 이렇게 위와 같이 texture 좌표계를 [0,1] 범위로 변환해주는 과정을 parameterization 이라고 합니다.
똑같은 설명인데 그러면 해상도에 따라서 실제로 texture 좌표계에서의 픽셀값은 동일한 값이라도 달라지게 될 것입니다.

그러므로 다른 해상도를 갖고 있는 이미지는 다른 결과를 야기할 것입니다.
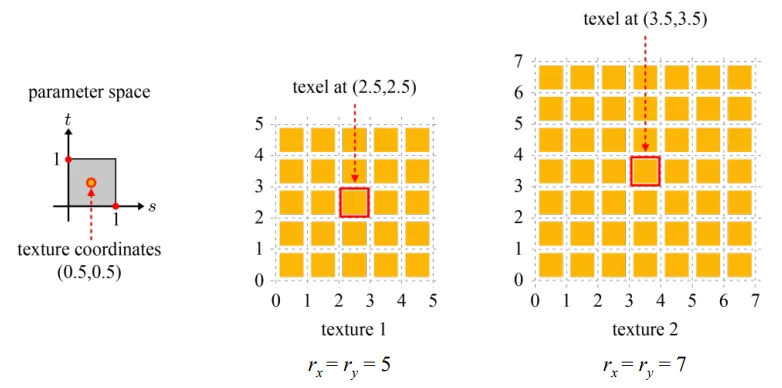
원통의 mesh같은 경우는 2D 좌표로 변환하는게 어렵지 않지만, 위의 그림처럼 사람의 얼굴인 경우 이를 2D 좌표로 변환하는 것은 어려울 수 있습니다. 이에 대해서 자세한 설명은 하지 않지만 실제로 쉽게 변환할 수 있는 방법이 연구돼서 사용중이라고 합니다.

사람의 몸 같은 mesh를 2D 좌표로 한번에 변환하기 보다는 얼굴 따로, 몸따로, 팔따로 이렇게 부분으로 나눠서 2D 좌표로 변환하는 방법이 더 쉽기 때문에 이렇게 여러개의 patches(부분)으로 나눠서 진행하게 됩니다. 이렇게 각 패치별로 아티스트는 texture를 입히게 됩니다. 참고로 patch는 chart라고 불리기도 합니다. 그리고 이러한 chart들이 모인 것을 atlas라고 합니다. Chart들이 여러개 모인 atlas로 변환될 때 좌표가 바뀐다는 점도 주의하셔야 합니다.
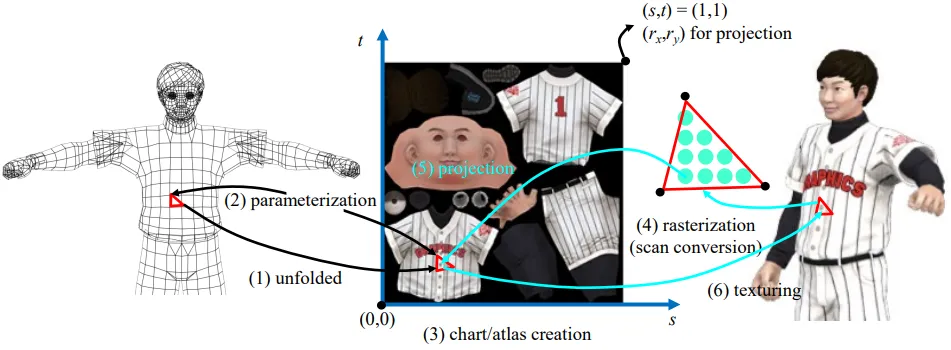
unfold : 3D mesh를 2D 좌표로 변환
Parameterization : Texture 좌표계를 [0,1]의 범위로 변환하는 과정
chart/atlas : 3D mesh를 여러개의 chart들로 분할하고, 이를 다시 하나의 texture image로 합쳐진 것을 atlas
raseterization(scan conversion) : 삼각형 안에 있는 fragment의 texture나 normal값을 꼭짓점으로부터 구하는 과정
projection : 각 fragment의 texture값이 update된 정보를 atlas에 전달
texturing : 최종적으로 atlas를 3D mesh에 매핑해주면서 texturing된 3d mesh 획득
Texture Wrapping

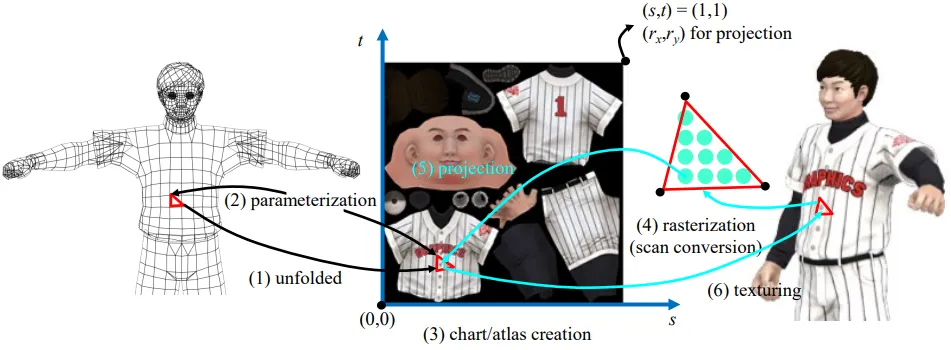
Texure 좌표를 parameterization을 통해서 [0,1]로 변환한다고는 하지만 꼭 [0,1]로 변환할 필요는 없습니다. 왜냐하면 위와 같이 빨간색 texture가 반복되는 3d mesh에 대해서 모든 부분을 [0,1]로 변환하고, 이에 대응되는 모든 texture 정보를 갖고 있는 다는건 비효율적입니다. 따라서 위와 같이 [0,1] 부분보다 넓은 영역을 지정하고, 하나의 texture 정보를 이용해서 이를 여러번 mapping하면 효율적으로 진행할 수 있습니다.
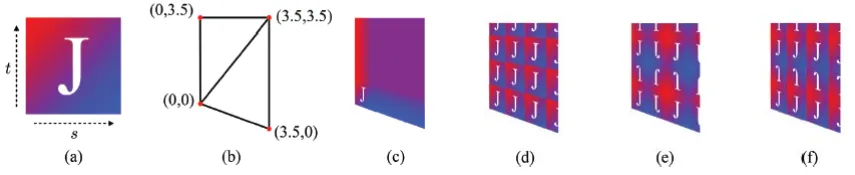
기본적으로 (a)부분을 [0,1]로 변환했을 때 지금 (b)를 보시면 s와 t의 좌표가 모두 3.5이기 때문에 1~3.5 범위는 모두 제거 될 것입니다. 이때 Texture Wrapping을 통해서 제거되는 부분의 값을 채워줄 수 있습니다.
Clamp-to-Edge : (c)그림을 보시면 1을 넘는 영역은 모두 1의 값을 갖도록 합니다.
Repeat: (d)의 그림을 보시면 타일들이 반복됩니다. 알고리즘은 1을 넘는 픽셀의 정수 값을 버리게 되어서 0~1의 값이 반복되게 됩니다.
Mirrored-Repeat: Repeat을 사용하면 경계 부분에서의 변화가 너무 뚜렷하게 보여서, 거울을 이용해서 texture를 대칭적으로 갖도록 하는 방식
Texture filtering
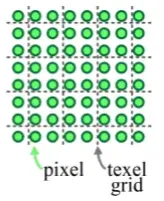
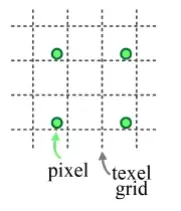
지금까지 저희가 Texture를 mapping할 때는 픽셀의 가운데 값을 이용한다고 했지만, 실제로는 정확히 가운데 값을 이용하지 않을 수도 있습니다. 이때는 주변 픽셀들의 정보를 잘 조합해서 픽셀값의 texture를 결정해야 되는데, 이 과정을 texture filtering 이라고 합니다.
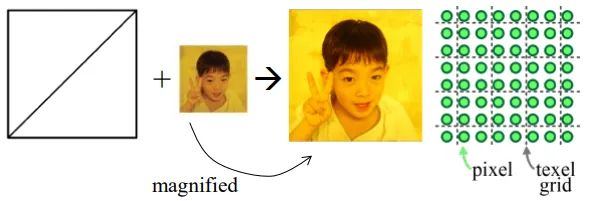
실제로 scrren-sapce 상에서 물체를 확대해서 texture map의 크기보다 큰 2D 좌표가 생성될 수도 있습니다. 이 경우 texture coordinate의 해상도보다 커지기 때문에 이를 확장해야 합니다. 이 과정을 magnification 이라고 합니다. 또한 기존까지 삼각형 안에 있는 fragment를 용어의 명확함을 위해서 잠시 pixel이라고 하도록 하겠습니다.
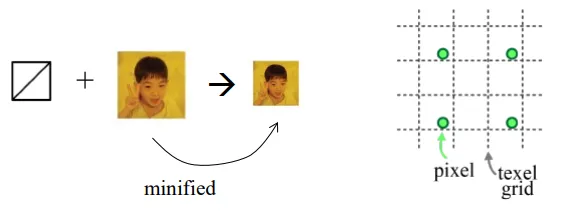
반대로 screen-space 상에서의 물체의 크기가 작아서 texture map의 해상도보다 작은 경우, texture map의 해상도를 줄이는 minification을 진행합니다.
Magnification

Texture의 크기가 더 작은 경우는 확대해야 하는 Magnfication부터 살펴보도록 하겠습니다. Texture map이 더 작기 때문에 하나의 texel안에 여러개의 pixel이 존재하게 됩니다. 이때 pixel은 해당하는 texel 값을 갖으면서 확대하는 경우를 Nearest point sampling 이라고 합니다. 이렇게 되면 단점으로 blocky image(계단 처럼 색을 갖고 있는게 보이는 현상)가 나타나게 됩니다.
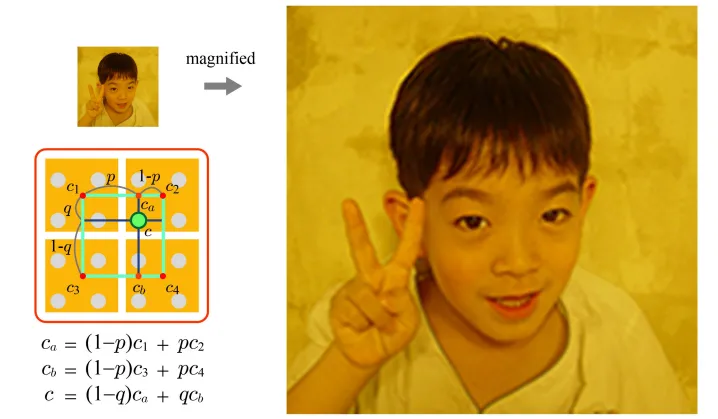
두번째 방법은 픽셀을 texel들의 Bilinear interpolation을 통해서 계산하는 방법입니다. 인접한 픽셀들의 정보를 모두 반영하기 때문에 blocky image의 문제점을 해결할 수 있습니다.
Minification
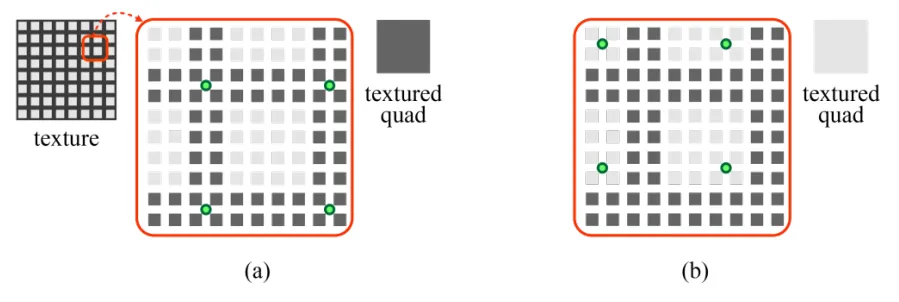
Texture가 더 큰 경우 픽셀 값들이 띄엄띄엄 선택하도록 작게 설정할 수 있습니다. 하지만 체커보드 texture를 사용한다고 했을 때 왼쪽의 경우 검정색만 나오게 될 것이고, 오른쪽의 경우는 흰색만 나오게 될 것입니다. 이러한 현상을 aliasing 이라고 합니다.
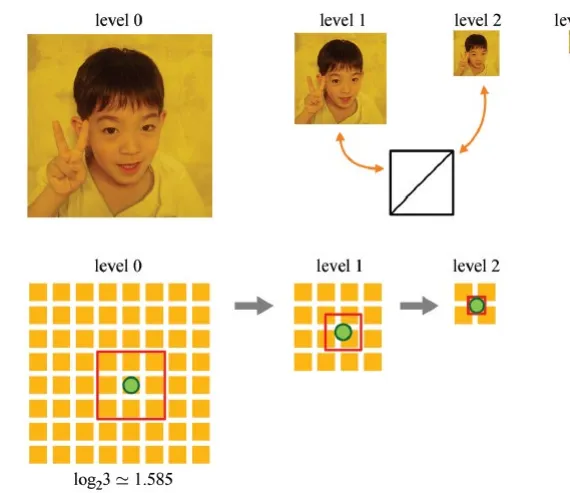
mipmap
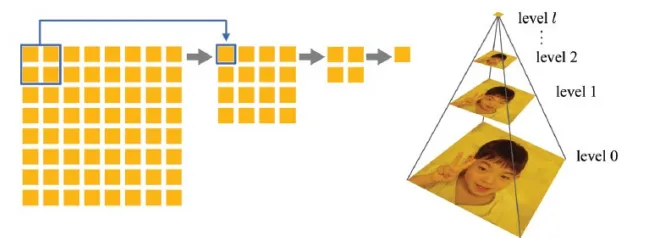
Aliasing 문제를 해결하기 위한 방법으로 mipmap 방식이 나왔습니다. Mipmap은 큰 해상도의 texture map을 여러 작은 해상도의 texture map으로 변경해서 모두 저장하도록 하는 방식입니다. 기본적으로 texture map의 해상도가 인 경우 (l+1) level까지 갖고 있도록 합니다. 이렇게 될 경우 적은 수의 픽셀 값이 존재하더라도 작은 texture map이 존재하기 때문에 minification 과정을 진행하지 않아도 됩니다.
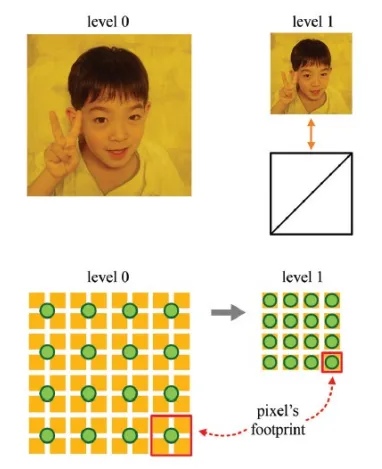
Texture map의 해상도를 낮추는 방법은 간단합니다. Projection된 픽셀이 차지하는 texel의 수만큼 더 낮은 texture map을 생성하고, 의 level을 선택하도록 합니다. 지금 예제에서는 4x4 texels가 하나의 픽셀에 대응되고 이때 정확히 level2의 값을 선택 되도록 했습니다. 이렇게 하나의 픽셀에 대응되는 texels를 footprint 라고 합니다.
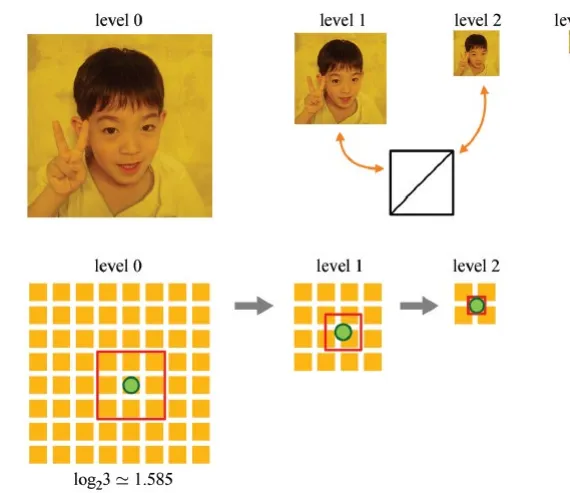
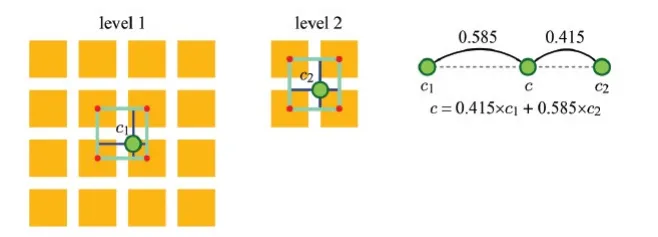
만약에 footpring가 3이면 어떻게 될까요? 3X3만큼 줄여가면서 texture map을 생성하는 과정은 동일합니다. 하지만 level이 정수가 아니라 은 1.585 값을 갖게 됩니다. 따라서 이러한 경우 의 값에 0.5를 곱한다음에 소수점을 버리게 됩니다. 지금 예시의 경우 1.585 + 0.5를 하고 소수점을 버려서 level2를 고르게 됩니다.
0.5를 더하지 않고 그냥 해당 값보다 작은 수 중 가장 큰 정수(1), 혹은 해당 값보다 큰 수 중 가장 작은 정수(2)를 고르는 방법도 존재합니다. 그리고 다시 확대하는 과정을 할 때 nearest sampling 혹은 bilinear interpolation 2가지 과정을 선택할 수 있습니다.
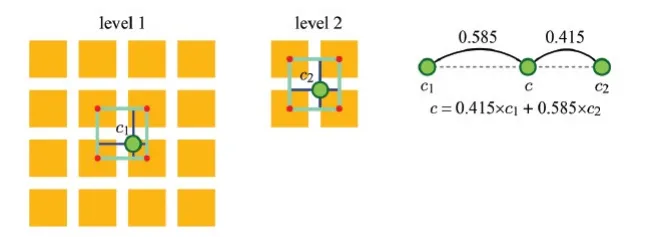
마지막으로 위의 과정처럼 2개의 celing(2), floor(1) 과정을 선택하고, 소수점은 interpolation으로 구하는 trilinear interpolation 과정도 존재합니다.
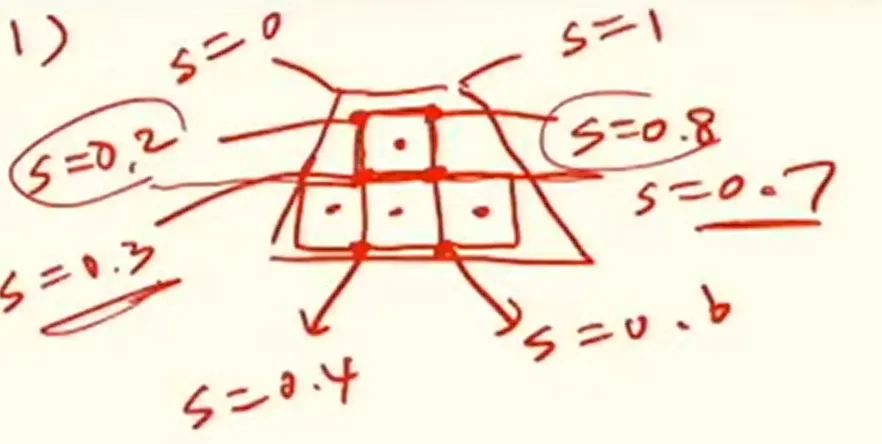
Mip map의 어려운 예시를 한번 살펴보도록 하겠습니다. 위의 그림은 screen space상에서의 3d mesh 입니다. 지금까지 mesh는 정사각형인 경우만 고려했지만 원근법을 고려하면 위와 같은 사다리꼴의 형태가 나올 수 있습니다. 이때 각 꼭짓점의 (s,t)의 좌표 중에서 s만 고려해보도록 하겠습니다. 맨위의 fragment에 대해서 대응되는 texture를 찾기 위해서 네모의 각 꼭짓점의 s값을 구하면 왼쪽위에서 부터 시계 방향으로 (0.2, 0.8, 0.7, 0.3)을 갖습니다.
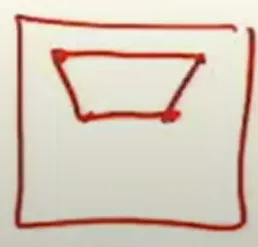
이에 대응되는 texture 좌표계에서의 footprint를 보면 사다리꼴 형태가 됩니다.
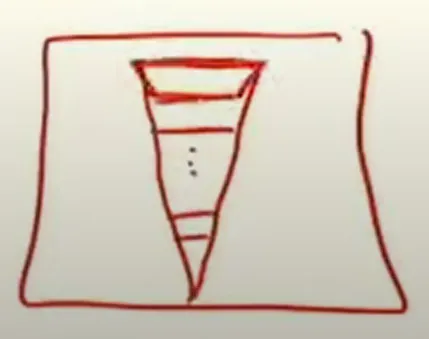
이렇게 대응되는 footpring를 모두 구했을 때 맨 윗부분은 texels의 개수가 더 많아서 minification이 진행 될 수 있지만, 맨 아래의 부분은 texel의 개수가 더 작아서 magnification이 진행될 수 도 있습니다. 즉 하나의 mesh에 대해서 minification과 magnification이 모두 진행 될 수 있습니다.
더 자세하게 복잡한 내용들이 존재하겠지만 사실 open GL이 알아서 해주기 때문에 이정도만 개념적으로 알고 넘어가도 괜찮습니다.
실제 사용 사례
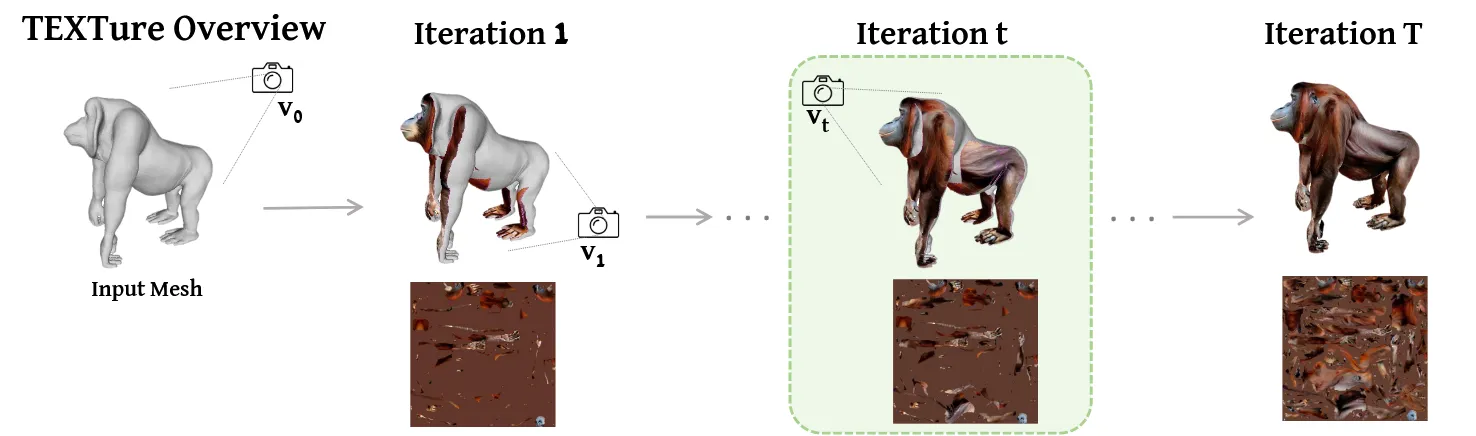
실제로 3D 데이터의 수가 적어서 2D diffusion 만큼의 성능이 나오지 않아서 2D diffusion 모델을 이용해서 3D를 학습하는 것은 잘 아실 것 입니다. 이때 Unfold를 통해서 얻은 UV map을 diffusion 모델로 업데이트 하고, 이후에 projection을 통해서 매핑하는 연구가 texture에서 흔하게 사용됩니다.
PBR Texture
https://caresser.tistory.com/36
PBR(Physical Base Rendering): 재질 표면에 따라 빛의 반사 정도가 물리적으로 어떻게 이루어지는지를 시물레이션하고 그것을 시각적으로 표현한 기법
Albedo(Diffuse, Base color)

- 가장 기본이 되는 재질 컬러 맵으로 그 재질이 갖고 있는 본연의 컬러를 표현
- 광학적 특성을 제외한 완전한 표면의 색만 표현하는 텍스처
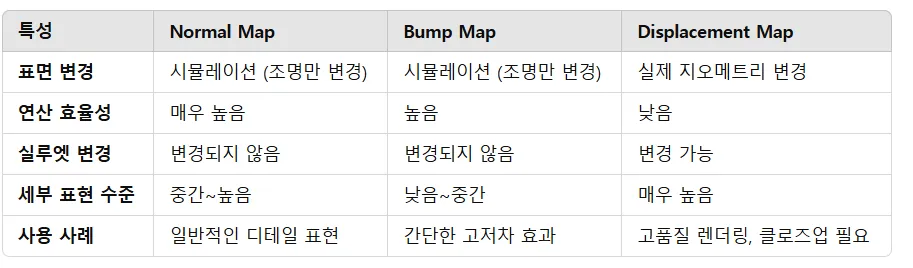
Normal, Bump, Displacement

- 3가지 방식 모두 표면의 디테일과 질감을 표현하는데 사용
- Normal map: 표면의 방향(노멀 벡터)을 픽셀 단위로 조정하여 조명과 그림자의 효과를 변화시킵니다.
- RGB 값은 X, Y, Z 방향의 노멀 벡터를 코딩한 것
- Bump map: 표면의 고저차를 흑백 이미지(grayscale)로 나타내어 간단한 질감을 표현
- 흑백 이미지의 밝기 값을 이용하여 높이 정보를 표현(밝은 부분: 표면이 돌출)
- Displacement map: 표면의 실제 지오메트리를 변경하여 물리적으로 정확한 높낮이와 디테일을 표현
- 흑백 이미지를 사용하여 표면의 vertex를 실제로 이동시킵니다.
Roughness(Glossiness)

- 외부의 빛이 재질에 부딪혀 반사될 때 그 양과 분산되는 정도를 설정
- grayscale 맵이고 white 부분이 roughness / black 부분이 smooth, glossy를 표현
- 예를들어서 유리는 빛을 좁은 영역에 강하게, 종이는 빛을 넓은 영역에 은은하게 반사합니다.
- 따라서 이를 적용했을 때 어느 부분에서 빛이 어느 정도 반사되는지, 광택도와 같은 요소들을 적용할 수 있습니다.
Metalness
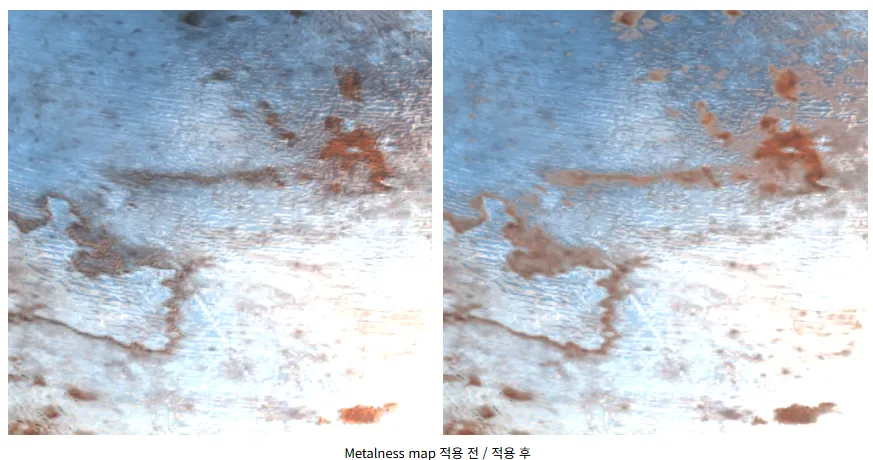
- 금속의 반사 특성과 비금속의 색상 특성을 현실적으로 표현하기 위해 필수적인 역할
- 금속의 반사 특성: 주변 환경의 색상과 빛을 반사
- 비금속 반사 특성: 반사된 빛과 기본 색상(diffuse)이 혼합
Specular(Reflection(반사))

- 빛이 표면에 반사되는 방식과 반사의 강도 및 색상을 제어
- 흑백 텍스처:
- 밝은 영역: 높은 반사율(예: 빛나는 부분)
- 어두운 영역: 낮은 반사율(예: 빛이 흡수되는 부분)
- 컬러 텍스처:
- 반사광에 특정 색상을 부여할 수 있음(예: 유리 표면에 색이 반사될 때)
Height

- Displacement map과 동일하게 간주 하지만 Height map은 지형과 같은 큰 지역의 표현에 주로 사용하고 Displacement map은 작고 세부적인 표현에 사용
Opacity

- 투명한 부분의 투명도와 범위를 조절할 수 있는 맵
- grayscale map이고 white는 불투명, black은 투명
Ambient Occlusion(AO)
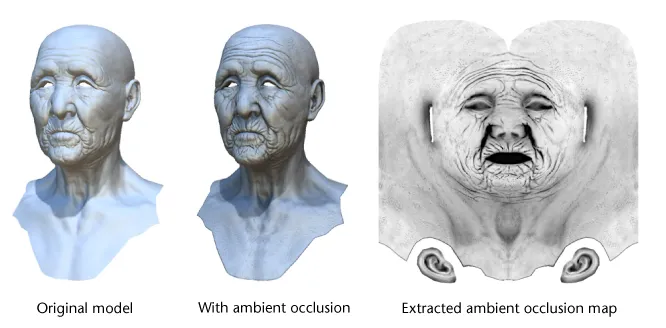
- 주변 환경에 반사되는 빛이 다시 영향을 주는 정도를 표현하기 위한 맵
- 구석이나 틈, 인물의 턱 아래처럼 어둡게 표현해야 하는 부분은 더욱 어둡게 표현할 수 있고 그에 따라 명도가 올라가는 효과
Refraction(굴절)

- 빛이 표면을 통과할 때 꺾이는(굴절되는) 방식과 꺾임의 강도를 정의하는 텍스처 맵
- 물속에 있는 물체를 표현하거나 투명한 유리 뒤에 보이는 물체를 표현할 때 사용
Self_Illumination (또는 Emissive)

- 스스로 빛을 발산하는 물체를 표현할 때 사용
- RGB 컬러 맵을 사용하고 베이스 컬러 바깥으로 발산하는 빛의 컬러와 양을 조절하기 위한 맵
