[ Top Interview 150 ] 169. Majority Element

귀찮Lee·2023년 8월 24일

[알고리즘] Top Interview 150

목록 보기

2/40

문제

Given an array nums of size n, return the majority element.

The majority element is the element that appears more than ⌊n / 2⌋ times. You may assume that the majority element always exists in the array.

Follow-up: Could you solve the problem in linear time and in O(1) space?

Input : 어떤 원소가 절반 이상을 차지하고 있는 nums
Output : 절반 이상을 차지하고 있는 원소 구하기
Follow-up : 공간 O(1), 시간 O(n) 으로 풀어보기
- 추가적인 배열 할당하여 사용 X, 크기에 따라 순회 시간이 liner하게 늘어나도록 해야 함

문제 풀이 고려 방안

구현이 쉬운 전략
- HashMap을 이용해 각 원소의 등장 횟수를 counting 한다
- 등장 횟수가 절반 이상이 되었을 때, 해당 원소를 return 한다.
위 전략의 문제점
- 해당 문제에서 Map 할당을 원치 않으므로 다른 방법을 생각해 봄
- 특정 원소가 절반 이상 들어있다는 특징을 이용하지 않음 (위 방법은 그냥 많은 원소 찾기 할때도 가능함)

풀이 방법 1 (Arrays Sort)

풀이 방법 분석
- 해당 배열을 정렬한다.
- 해당 원소가 절반 이상을 차지하므로 가운데에는 반드시 해당 원소가 나온다.

풀이 코드

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        int n = nums.length;
        return nums[n/2];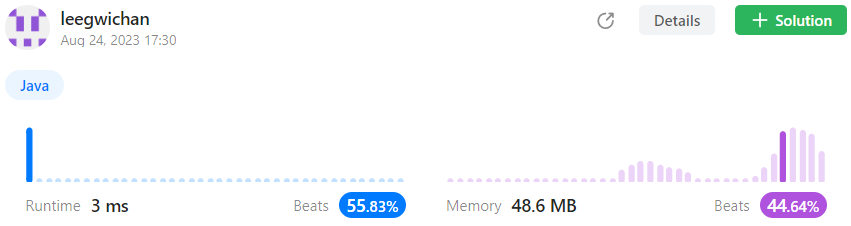
    }
}

풀이 방법 2 (HashMap)

위의 "문제 풀이 고려 방안"에서 언급한 방법

class Solution {
    public int majorityElement(int[] nums) {
        int n = nums.length;
        Map<Integer, Integer> map = new HashMap<>();

        for (int i = 0; i < n; i++) {
            map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        }

        n = n / 2;
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            if (entry.getValue() > n) {
                return entry.getKey();
            }
        }

        return 0;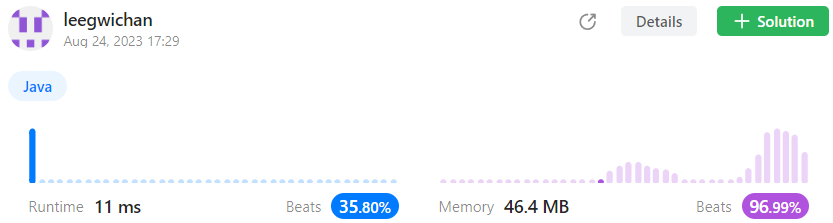
    }
}

풀이 방법 3 (Moore Voting Algorithm)

Moore Voting Algorithm
- 배열에 포함된 원소들 중 절반 이상 포함된 원소를 linear time 과 constant space 로 찾을 수 있는 알고리즘
- 스트리밍 알고리즘(streaming algorithm)의 대표적인 예
- 만약 배열 내에 과반수 만큼 등장하는 원소가 없다면 결과값으로 임의의 의미없는 값이 나오게 된다
Moore Voting Algorithm 동작 방식
- major 와 count 를 0 으로 초기화 한다.
- 전 원소를 순회하면서
  - count가 0인 경우 major를 교체 한다.
  - major 와 현재 원소가 같으면 count를 1 추가한다.
  - major 와 현재 원소가 같지 않으면 count를 1 감소한다.

풀이 코드

class Solution {
    public int majorityElement(int[] nums) {
        int count = 0;
        int major = 0;

        for (int num : nums) {
            if (count == 0) {
                major = num;
            }
            if (major == num) {
                count++;
            } else {
                count--;
            }
        }
        return major;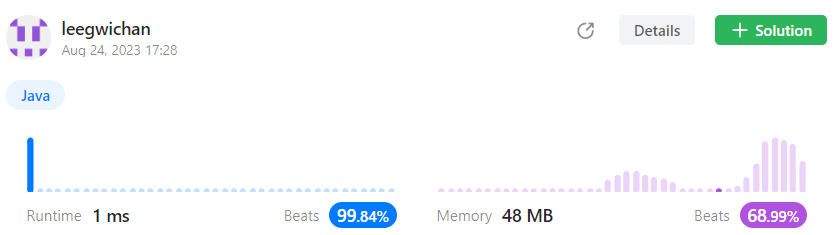
    }
}

결과 비교

빠른 순서 : Moore Voting - Arrays Sort - Hash Map
- Moore Voting 자체는 배열을 한번만 순회함 O(N)
- Arrays Sort는 JDK에서 지원하기 때문에 일반적으로 O(NlogN)의 시간 복잡도를 가짐
메모리 사용량 효율순 : Hash Map - Moore Voting - Arrays Sort
- Hash Map 방법 자체가 모든 면에서 안 좋을 줄 알았는데, 메모리에서는 가장 좋았다.

총 정리 & 나의 생각

Arrays Sort : JDK 자체에서 기능을 지원해주므로 코드의 양은 가장 적다.
- 내가 이 방법을 떠올리지 못한 이유는 최소한의 변형이 가장 성능이 좋을 것이라는 착각을 했던 것 같다.
HashMap
- HashMap을 초기 설정할 때 배열을 순회하면서 설정하는 시간이 걸리므로 무조건적으로 않좋은 것이라는 편견이 있었던 것 같다.
Moore Voting Algorithm : 특정 상황에서만 사용할 수 있는 알고리즘이므로 성능은 좋지만 다른 용도로서 거이 사용할 수 없다.
- 해당 방법을 혼자서 떠올리기 위해 노력했는데 쉽지 않았다. 여러 문제를 풀면서 기존에 많은 알고리즘들을 배워야 겠다는 생각을 했다.