[ Top Interview 150 ] 909. Snakes and Ladders

문제

909. Snakes and Ladders

• 왼쪽 아래에서 시작해서 뱀처럼 올라가는 Board가 주어진다.
• 출발지는 왼쪽 최하단이며, 목적지는 최상단 가장 왼쪽 혹은 가장 오른쪽이다.
• 한 번에 아래 행동을 순서대로 한 번 실시한다.
  1. 주사위를 굴려 해당 칸만큼 이동한다.
  2. 각 칸에는 숫자가 쓰여있는데 -1이 있을 경우 그 턴에는 이동하지 않는다. -1이 아닌 경우 해당 숫자로 이동한다. (더 앞 혹은 더 뒤로 이동할 수 있다.)
     • 주사위를 던진 후 칸에 도착하여 다른 숫자로 이동하는 것은 한 번 실행한다
• 출발지에서 시작하여 목적지에 도착하는 최소 턴 수를 반환하라
  • 만약 도착지에 도달할 수 없다면, -1을 반환함

예시

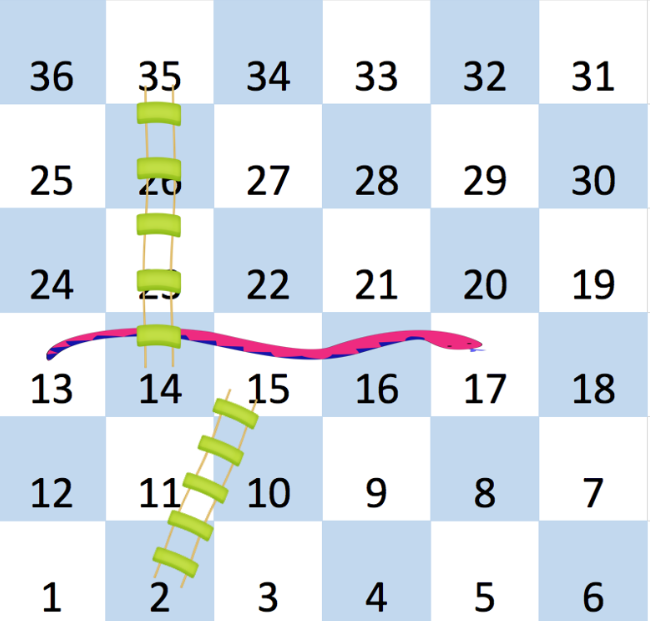
• Input : board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
• Output : 4
  • 최소 경로 : 2(->15) -> 17(->13) -> 14(->25) -> 36

알고리즘 전략

• 기본 전략 : 방향 graph

  • 각 칸에서 다음 칸으로 갈 수 있는 칸들을 방향 Graph 형식으로 가진다.
  • 다뤄야 하는 칸 수가 많아질 수 있으므로 Map<Integer, Set<Integer>> 형식으로 graph를 만든다.

• 1단계 전략. board를 통해 graph 만들기 (makeGraph())

  1. int[][] 형식의 board는 파악하기 어려우니, int[]형식으로 전환함 (함수 getValue()로 구현
  2. 1번부터 $n^2$까지 순회하면서 1~6칸 이동했을 때, 있을 수 있는 다음 칸을 Set<Integet>형식으로 만들어 Map에 넣는다.
     • 칸 수 만큼 이동했을 때, value가 -1이면 해당 위치 아니면 value를 넣는다.

• 2단계 전략. graph를 통해 최소 횟수 탐색 (BFS, findMinimumCount())

  1. 1에서 시작함
  2. 현재 위치(들)에서 갈 수 있는 다음 칸들을 탐색
  3. 다음 칸들이 다시 현재 위치가 되며 도착지가 나올 때까지 반복
     • 특정 횟수 (총 칸수 / 6 + 1)만큼만 반복하고 안되면 -1을 반환함

1차 작성 코드

• Time complexity : $O(n^2)$ (graph 탐색에서 중복으로 탐색되는 경우가 있음)
• Space complexity : $O(n)$

class Solution {

    private static final int MAX_DICE = 6;
    private static final int NO_MOVE = -1;
    private static final int NOT_FINISH = -1;

    public int snakesAndLadders(int[][] board) {
        int destination = board.length * board[0].length;
        Map<Integer, Set<Integer>> graph = makeGraph(board);
        return findMinimumCount(graph, destination);
    }

    private Map<Integer, Set<Integer>> makeGraph(int[][] board) {
        int[] values = getValues(board);
        int destination = values.length;

        Map<Integer, Set<Integer>> graph = new HashMap<>();
        for (int index = 0; index < values.length - 1; index++) {
            Set<Integer> nextNodes = new HashSet<>();
            for (int dice = 1; dice <= MAX_DICE; dice++) {
                if (index + 1 + dice > destination) {
                    break;
                }
                int next = values[index + dice] == NO_MOVE ? index + 1 + dice : values[index + dice];
                nextNodes.add(next);
            }
            graph.put(index + 1, nextNodes);
        }

        return graph;
    }

    private int[] getValues(int[][] board) {
        int[] values = new int[board.length * board[0].length];
        for (int i = 0; i < values.length; i++) {
            values[i] = getBoardValue(board, i);
        }
        return values;
    }

    private int getBoardValue(int[][] board, int index) {
        int rowIndex = index % board.length;
        int columnIndex = index / board.length;

        if (columnIndex % 2 == 0) {
            return board[board.length - 1 - columnIndex][rowIndex];
        } else {
            return board[board.length - 1 - columnIndex][board.length - 1 - rowIndex];
        }
    }
    
    private int findMinimumCount(Map<Integer, Set<Integer>> graph, int destination) {
        Set<Integer> nodes = new HashSet<>();
        nodes.add(0);
        int moveCount = 1;

        while (moveCount < destination) {
            Set<Integer> nextNodes = new HashSet<>();
            for (int node : nodes) {
                if (graph.get(node).contains(destination)) {
                    return moveCount;
                }
                nextNodes.addAll(graph.get(node));
            }
            nodes = nextNodes;
            moveCount++;
        }

        return NOT_FINISH;
    }
}

2차 작성 코드

• 기존 문제점 & 해결 방안

  • 다음에 갈 수 있는 곳을 모두 포함하다보니 이미 탐색된 Graph도 반복적으로 탐색하게된다.
  • 탐색한 Node를 관리하는 repository를 관리하여 중복적으로 탐색하지 않도록 함

• Time complexity : $O(n)$ (graph 탐색에서 중복되는 경우가 없어짐)

• Space complexity : $O(n)$

    // 나머지 함수는 1차 작성 코드와 동일
  
    private int findMinimumCount(Map<Integer, Set<Integer>> graph, int destination) {
        Set<Integer> nodes = new HashSet<>();
        Set<Integer> repository = new HashSet<>();
        nodes.add(0);
        repository.add(0);
        int move = 1;
        int maxMove = destination / MAX_DICE + 1;

        while (move <= maxMove) {
            Set<Integer> nextNodes = new HashSet<>();
            for (int node : nodes) {
                if (graph.get(node).contains(destination)) {
                    return move;
                }
                
                for (int lowerNode : graph.get(node)) {
                    if (!repository.contains(lowerNode)) {
                        nextNodes.add(lowerNode);
                        repository.add(lowerNode);
                    }
                }
            }
            nodes = nextNodes;
            move++;
        }

        return NOT_FINISH;
    }

모범 답안 찾아보기

• 모범 답안 링크

• getValues()

  // 내 답안
      private int[] getValues(int[][] board) {
          int[] values = new int[board.length * board[0].length];
          for (int i = 0; i < values.length; i++) {
              values[i] = getBoardValue(board, i);
          }
          return values;
      }
  
      private int getBoardValue(int[][] board, int index) {
          int rowIndex = index % board.length;
          int columnIndex = index / board.length;
  
          if (columnIndex % 2 == 0) {
              return board[board.length - 1 - columnIndex][rowIndex];
          } else {
              return board[board.length - 1 - columnIndex][board.length - 1 - rowIndex];
          }
      }
  
  // 모범 답안
      private short[] getValues(int[][] board) {
          short[] boardValues = new short[destination + 1];
          int boardIndex = 1;
          for (int row = n - 1; row >= 0; row--) {
              for (int col = 0; col < n; col++)  {
                  boardValues[boardIndex++] = (short)board[row][col];
              }
  
              row--;
              if (row < 0)  {
                  break;
              }
  
              for (int col = n - 1; col >= 0; col--)  {
                  boardValues[boardIndex++] = (short)board[row][col];
              }
          }
  
          return boardValues
      }

• graph를 통해 최소 횟수 탐색 방법

  • 나의 답안 : Set을 매번 만들어 후보군을 전부 넣는 방식으로 구현
  • 모범 답안 : Queue 형식과 1 ~ $n^2$ 사이의 수만 사용한다는 점을 이용
    • 현재 Node 보관 방식 : int[]와 readIndex, writeIndex를 이용하여 Queue 방식과 유사하게 사용했다.
    • 이미 방문했는지 확인하는 방식 byte[] count를 크기를 $n^2$만큼 만들어 count[node] == 1의 형식으로 이미 방문한 노드인지 확인함

  // 내 답안
  private int findMinimumCount(Map<Integer, Set<Integer>> graph, int destination) {
          Set<Integer> nodes = new HashSet<>();
          Set<Integer> repository = new HashSet<>();
          nodes.add(0);
          repository.add(0);
          int move = 1;
          int maxMove = destination / MAX_DICE + 1;
  
          while (move <= maxMove) {
              Set<Integer> nextNodes = new HashSet<>();
              for (int node : nodes) {
                  if (graph.get(node).contains(destination)) {
                      return move;
                  }
  
                  for (int lowerNode : graph.get(node)) {
                      if (!repository.contains(lowerNode)) {
                          nextNodes.add(lowerNode);
                          repository.add(lowerNode);
                      }
                  }
              }
              nodes = nextNodes;
              move++;
          }
  
          return NOT_FINISH;
      }
  
  // 모범 답안
  
  final int bfsQueueLen = Math.min(n * n, 8 * n);
  short[] bfsQueue = new short[bfsQueueLen];
  int readIndex = 0;
  int writeIndex = 0;
  bfsQueue[writeIndex++] = 1;  // Initialize BFS queue to start at square #1
  
  byte[] count = new byte[endSquare + 1];
  count[1] = 1;                   // Mark the starting location as already visited.
  
  while (readIndex != writeIndex) {
      int currSquare = bfsQueue[readIndex++];
      readIndex %= bfsQueueLen;
  
      int maxOpenMove = 0;
      for (int move = 6; move >= 1; move--) {
          int nextSquare = currSquare + move;
          if (brd[nextSquare] >= 0) {
              if ((nextSquare = brd[nextSquare]) == endSquare)  return count[currSquare];
          } else {
              if (move < maxOpenMove)  // If we already moved to an open square 1 to 6
                  continue;
              maxOpenMove = move;
          }
  
          if (count[nextSquare] == 0) {
              count[nextSquare] = (byte)(count[currSquare] + 1);
              bfsQueue[writeIndex++] = (short)nextSquare;
              if ((writeIndex %= bfsQueueLen) == readIndex)  return 0; // Queue overflow
          }
      }
  }
  
  return -1;

모범 답안 개선 (자료구조를 Custom 하여 사용하기)

• 모범 답안에서 문제점

  • Queue의 형식을 사용하는데, 내부 구조를 Main Logic에서 관리하여 사용하기 때문에 모범답안을 보고 이해하기 힘들다.
  • Queue 관련 코드와 이동 관련 코드가 섞여 있어 수정 및 이해가 힘들다.

• 개선 방안

  • Queue 구조의 자료 구조를 직접 구현한다.
  • 동작 원리는 모범 답안의 코드를 따르고, 특정 원소가 중복이 되었는지도 내부에서 판단하도록 한다.

• 내가 만든 Custom 자료 구조

  class UniqueIntegerQueue {
  
      private static final int ALREADY_VISIT = 1;
  
      private final int max;
      private final byte[] count;
      private final int[] queue;
      private int readIndex = 0;
      private int writeIndex = 0;
  
      UniqueIntegerQueue(int max) {
          this.max = max;
          this.count = new byte[max + 1];
          this.queue = new int[max];
      }
  
      boolean add(int value) {
          validateValue(value);
          if (count[value] == ALREADY_VISIT) {
              return false;
          }
  
          queue[writeIndex++] = value;
          count[value] = ALREADY_VISIT;
          return true;
      }
  
      int remove() {
          if (size() <= 0) {
              throw new IllegalStateException();
          }
  
          return queue[readIndex++];
      }
  
      int size() {
          return writeIndex - readIndex;
      }
  
      private void validateValue(int value) {
          if (value < 0 && value > max) {
              throw new IllegalArgumentException();
          }
      }
  }

• Custom 자료 구조를 이용한 답안

  class Solution {
  
    private static final int NO_MOVEMENT = -1;
    private static final int NOT_EXIST = -1;
    private static final int MAX_DICE = 6;
  
    public int snakesAndLadders(int[][] board) {
  
        int destination = board.length * board[0].length;
        short[] boardValues = makeGraph(board);
        return findMinimumCount(boardValues, destination);
    }
  
    private short[] makeGraph(int[][] board) {
  
        final int n = board.length;
        final int destination = n * n;
  
        short[] boardValues = new short[destination + 1];
        int boardIndex = 1;
        for (int row = n - 1; row >= 0; row--) {
            for (int col = 0; col < n; col++)  {
                boardValues[boardIndex++] = (short)board[row][col];
            }
  
            row--;
            if (row < 0)  {
                break;
            }
  
            for (int col = n - 1; col >= 0; col--)  {
                boardValues[boardIndex++] = (short)board[row][col];
            }
        }
        
        return boardValues;
    }
  
    private int findMinimumCount(short[] boardValues, int destination) {
        UniqueQueueUnderPositiveInteger queue = new UniqueIntegerQueue(destination);
        queue.add(1);
        int movingCount = 1;
  
        while (queue.size() > 0) {
            int size = queue.size();
            for (int count = 0; count < size; count++) {
                int position  = queue.remove();
                for (int dice = 1; dice <= MAX_DICE; dice++) {
                    int nextPosition = boardValues[position + dice] == NO_MOVEMENT
                            ? position + dice : boardValues[position + dice];
  
                    if (nextPosition == destination) {
                        return movingCount;
                    }
                    queue.add(nextPosition);
                }
            }
  
            movingCount++;
        }
  
        return NOT_EXIST;
    }