Algorithm(알고리즘) - 1

◎ Algorithm(알고리즘)

• Algorithm

  • Algorithm : 문제를 해결하는 최선의 선택
  • 컴퓨터를 이용해 문제를 해결할 때에는, 무수히 많은 방법을 시도할 수 있다.
  • 모든 경우를 하나씩 비교하여 그중에서 최선을 골라낼 수 있음
  • 이외 방법론적인 부분은 여러가지가 있다.

• 우리의 목표

  • 컴퓨터의 문제 해결 방식 이해
  • 최선의 선택을 찾는 방법 알기

• 알고리즘을 구상하는 법

  • step1 문제를 이해
    • 현재(코딩 테스트)의 문제의 설명과 입출력예시, 제한사항, 그리고 주의사항을 보고 문제가 무엇인지 이해함
  • step2 문제를 어떻게 해결할 수 있을지, 전략을 세움
    • 연습장에 전체적인 그림을 그려가면서 전체적인 흐름을 알아감
    • 수도코드 작성 전, 인간의 사고로 문제를 해결
    • 코드를 작성하기전, 수도코드 작성
  • step3 문제를 코드로 옮김
    • 위에서 세운 전략을 코드로 옮김
    • 구현한 코드를 논의(생각)를 통해 구현한 코드 최적화

◎ 의사코드 작성법

• 의사코드

  • 프로그래밍 언어로 코드를 작성하기 전에 우리가 쓰는 일상 언어로 프로그램이 작동하는 논리를 먼저 작성하는 것
  • 문제를 이해하고 논리 문제를 풀듯이 풀어보고, 컴퓨팅 사고로 전환하여 의사코드를 작성하고 개발 언어로 코드를 작성

• 의사코드 작성시 장점

  • 시간이 단축
    • 문제가 복잡해지거나 코드의 양이 길어진다면 시간이 지나면서 세세한 로직은 기억하기 힘들다.
    • 본인이 생각한 코드를 수도 코드로 남겨놓는다면, 지표가 되어 헤매는 시간이 줆
  • 디버깅에 용이
    • 어느 부분에서 오류가 났는지 확인할 때, 모국어로 쓰인 의사코드를 확인하여 다른 것을 제외한 로직에 신경 쓸 수 있다.
  • 프로그래밍 언어를 모르는 사람과 소통할 수 있다.
    • 프로그래밍 언어에 익숙하지 않은 사람도 나의 수도 코드를 보며 이해하는데 도움이 됨

• 의사코드 작성시 주의사항

  • 사람이 생각할 수 있는 상상력의 부분은 최대한 배제하고, 빈틈없이 의사코드를 작성할 것

• 의사코드 작성 양식

  • 다른 사람도 이해할 수 있는 자연어(영어나 한국어처럼 일상에서 사용되는 언어)만 사용
  • 자연어와 프로그램 언어의 조합

  // 집에서 TV를 본다. (X)
  
  // 내 장소가 집이 아니라면, 집까지 도달하는 과정 필요  // if ( 내 장소 != 집 ) 집까지 가는 과정 필요
    // 현재 위치에서 집까지 가는 길 파악
    // 집까지 도달하기 위한 최적의 방법 파악
    // 행위 실행, 이후 현관문에 도착에 현관문을 연다.
  // 거실에 도착하는 방법 파악
    // 현재 집안 위치에서 거실까지 가는 방법 파악
    // 만약, 가는 길에 닫힌 문이 있다면, 문을 열고 다시 진행
    // TV 리모콘 위치 파악 및 리모콘으로 전원 ON
    // 근처 쇼파에 앉고, 시선을 TV로 향함

◎ 시간복잡도(Time Complexity)

• 시간복잡도(Time Complexity)

  • 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는 것을 수치화한 것

• 시간 복잡도 표기 방법

  • Big-O(빅-오) : 최악의 경우에 대비하여 나타냄
  • Big-Ω(빅-오메가) : 최선의 경우에 대비하여 나타냄
  • Big-θ(빅-세타) : 중간(평균)의 경우에 대비하여 나타냄
  • 최선, 중간의 경우보다 "이 정도 시간까지 걸릴 수 있다"를 고려해야 그에 맞는 대응이 가능하다. 따라서 Big-O 표기법을 많이 사용

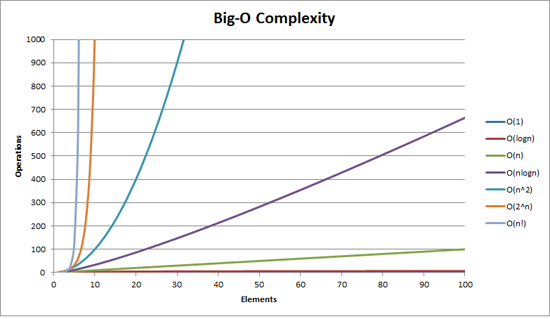
• Big-O 표기법의 종류 (n : 데이터 크기, 선 위가 상대적으로 효율적)

  • O($1$) : n에 상관받지 않고 똑같은 실행시간이 걸림
  • O($n$) : 데이터 크기에 비레하여 늘어감 (2n, 3n, ... 의 경우도 똑같이 표기)
  • O($log n$) : 데이터의 크기가 특정 배수씩 늘었을 때, 하나씩 커지는 경우

    ---

  • O($n^2$) : 데이터가 늘어남에 따라 제곱배로 늘어남 ($n^3$, $n^4$ ... 의 경우, n이 많이 늘어나도 차이 없으므로 똑같이 표현)
  • O($c^n$) : 데이터가 하나 늘어날 경우, 이전보다 c배 늘어나는 경우
  • O($n!$)

• 데이터 크기에 따른 시간 복잡도 예시