Search Algorithm

◎ Tree traversal(트리 순회)

• Tree traversal(트리 순회)

  • 특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것
  • 트리 구조는 계층적 구조라는 특별한 특징을 가지기 때문에, 모든 노드를 순회하는 방법엔 크게 세 가지가 있다.
  • 트리 구조에서 노드를 순차적으로 조회할 때의 순서는 항상 왼쪽부터 오른쪽이다.

• 이진 트리를 순회하는 3가지 방법

  • 전위 순회 (preorder traverse)
    • 자신의 값 파악 -> 왼쪽 노드로 가서 전부 확인 -> 오른쪽 노드로 가서 전부 확인
  • 중위 순회 (inorder traverse)
    • 왼쪽 노드로 가서 전부 확인 -> 자신의 값 파악 -> 오른쪽 노드로 가서 전부 확인
  • 후위 순회 (postorder traverse)
    • 왼쪽 노드로 가서 전부 확인 -> 오른쪽 노드로 가서 전부 확인 -> 자신의 값 파악

◎ 그래프 탐색(BFS / DFS)

• 그래프 탐색

  • 하나의 정점에서 시작하여 그래프의 모든 정점들을 한 번씩 방문(탐색)하는 것이 목적
  • 원하는 자료를 찾으려면, 하나씩 모두 방문하여 찾아야 한다. (정렬되어 있지 않으므로)

• BFS(Breadth-First Search)

  • Breadth-First Search : 너비를 우선적으로 탐색하는 방법
  • 정점 한곳에서 depth가 1인 곳부터 시작해서 점점 깊은 곳을 탐색하는 방법
  • 주로 두 정점 사이의 최단 경로를 찾을 때 사용
  • 단점 : 만약, 경로를 하나씩 전부 방문한다면, 최악의 경우에는 모든 경로를 다 살펴보아야 한다.

• DFS(Depth-First Search)

  • Depth-First Search(깊이 우선 탐색) : 하나의 경로를 끝까지 탐색한 후, 해당 조건이 아니라면 다음 경로로 넘어가 탐색
  • 하나의 노선을 끝까지 들어가서 확인하고 다음으로 넘어가기 때문에, 운이 좋다면 단 몇 번 만에 경로를 찾을 수 있다.
  • 장점 : 해당 길이 아님을 미리 체크할 수 있다면, 바로 그 순간 다음 탐색으로 넘어갈 수 있습니다.
  • 단점 : 경우에 따라, 해당 경우를 찾더라도, 다른 모든 경로를 살펴보아야 한다, 시간이 BFS보다 상대적으로 오래 걸릴 수 있다.

• BFS, DFS 예시

  • 꼭 graph, tree 구조에서만 한정하여 사용하는 것이 아니라 일종의 방법론이다.
  • DFS

  // DFS (깊이 우선 탐색 - 재귀 이용)
  // 충분히 변형하여 사용하여야 함
  public class Solution {
    int goalLen;
    String ans;
  
      public String barcode(int len) {
      this.goalLen = len;
      BarcodeNode firstNode = new BarcodeNode("1");
  
      findAns(firstNode);
      return ans;
  
      }
  
    // 특정 조건 만족하는 것을 찾을 시, 바로 return
    public boolean findAns(BarcodeNode node){
      // 현재 노드 조건 충족 확인 / 미충족시, false
      if (!node.passCondition()) return false;
      // (길이 + 조건 통과시 true, 멤버 변수에 저장)
      if (node.info.length() == this.goalLen){
        this.ans = node.info;
        return true;
      }
  
    // 왼쪽 노드 false시, 오른쪽 노드 실행
    // 오른쪽 노드 fales시, false
      node.makeLowerClass();
      if(!findAns(node.left)){
        if(!findAns(node.right)){
          return false;
        }
      }
      return true;
    }
  }

  • BFS
    

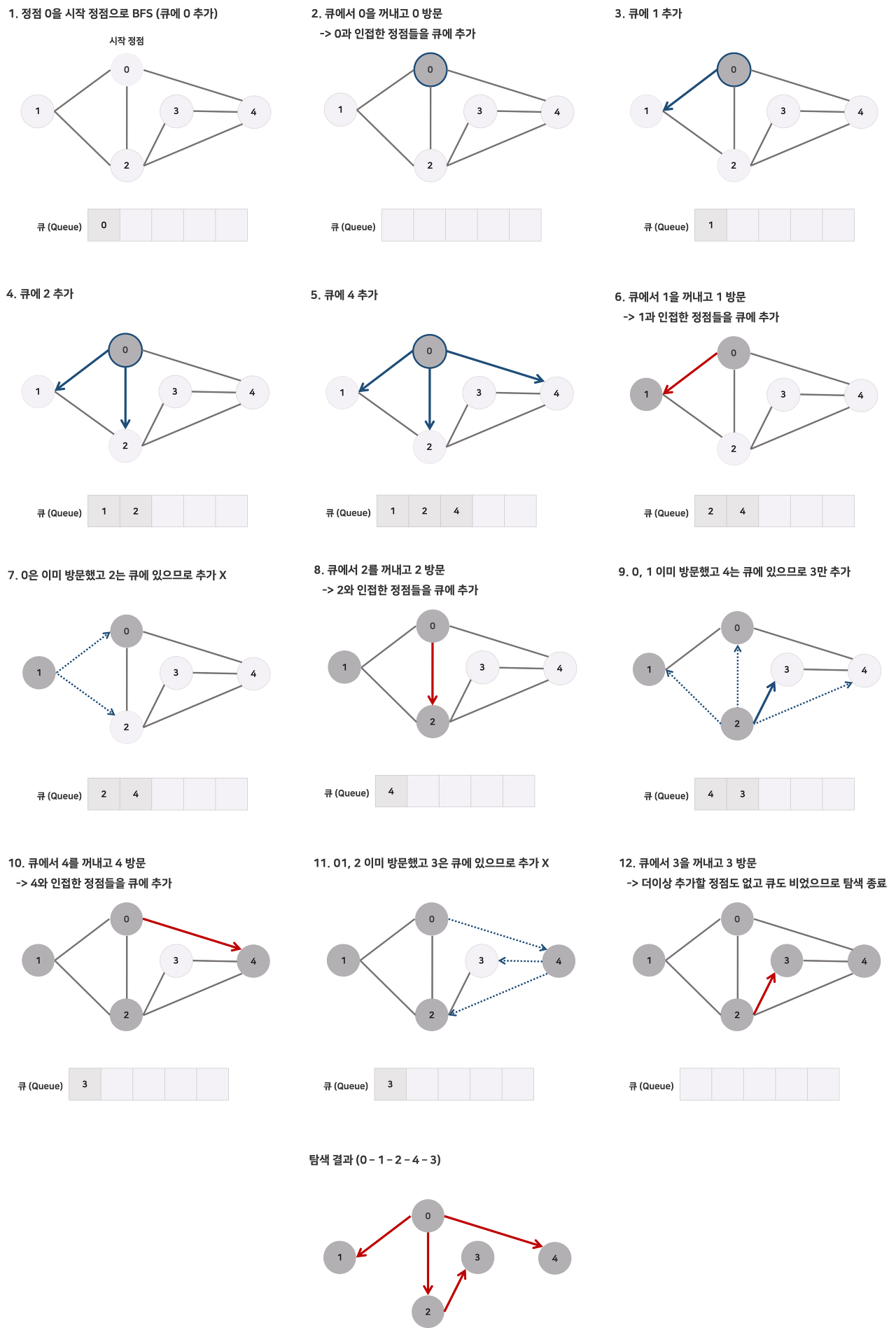
  // BFS (너비 우선 탐색 - Queue 사용)
  public int connectedVertices(int[][] adjaMatrix) {
      if (adjaMatrix.length == 1) return 1;
  
      int count = 0; // 초기화
      // 현재 탐색중인 queue
      Queue<Integer> queue = new LinkedList<>(); 
      // 아직 탐색하지 않은 요소를 가지고 있음
      HashSet<Integer> pointSet = new HashSet<>(); 
      for(int i=0; i<adjaMatrix.length; i++){
        pointSet.add(i);
      }
  
      while (pointSet.size() != 0){ // 탐색하지 않은 요소가 남아있을 때
        Integer firstpoint = (Integer) pointSet.toArray()[0]; // 한개 고름
        pointSet.remove((Integer) firstpoint); // 탐색하지 않은 요소에서 제거
        queue.add(firstpoint); // 현재 탐색할 요소에 등록
  
        while(!queue.isEmpty()){ // 현재 탐색할 요소에 무언가 있을 경우
          Integer aPoint = queue.poll(); // 현재 탐색할 거 가져옴
          for (int i=0; i < adjaMatrix.length; i++){
            // 인접 요소가 있음 && 현재 미탐색
            if (adjaMatrix[aPoint][i] == 1 && pointSet.contains(i)){ 
              pointSet.remove((Integer) i); // 현재 탐색안한 대상에서 제외
              queue.add(i); // 현재 탐색할 대상에 추가 -> 깊이가 낮은것부터 반복문에 의해 탐색할 예정
            }
          }
        }
  
        count++;
      }
      return count;
    }