◎ 재귀 함수(Recursive Function)
- 함수가 직접 또는 간접적으로 자신을 호출하는 프로세스
- 재귀함수도 종료지점을 제대로 생각하지 않고 구현을 하면 스택오버플로우가 발생할 수 있으니 항시 주의해서 구현해야함
- 재귀 호출 : 한 메서드가 실행과정 중에 자기 자신을 호출한 경우
public class RecursiveFunctionExample01 {
public static void main(String[] args) {
System.out.println(PlusPlus(5));
}
public static int PlusPlus(int n) {
if(n == 0) return 0;
return n += PlusPlus(n-1); // 재귀함수 시작
}
}◎ 재귀문 쉽게 작성하는 법
-
예시) 0,0,0,0,0 부터 2,2,2,2,2까지 콘솔창에 찍어내기
-
첫째, 기존의 문제에서 출발하여 더 작은 경우 (이전 단계)를 생각합니다.
- 2,2,2,2,1 -> 2,2,2,2,2
-
둘째, 같은 방식으로, 문제가 더는 작아지지 않을 때까지 더 작은 경우(이전 단계)를 생각합니다.
- 0,0,0,0,0 -> 0,0,0,0,1 -> 0,0,0,0,2 ->,0,0,0,1,0
-> ... -> 2,2,2,2,2
- 0,0,0,0,0 -> 0,0,0,0,1 -> 0,0,0,0,2 ->,0,0,0,1,0
-
셋째, 문제가 간단해져서 바로 풀 수 있게 되는 순간부터 앞서 생성한 문제를 차근차근 해결
int maxNum = 2; if (m != maxNum) {m++;} else if (l != maxNum) {m=0; l++;} else if (k != maxNum) {m=0; l=0; k++;} else if (j != maxNum) {m=0; l=0; k=0; j++;} else if (i != maxNum) {m=0; l=0; k=0; j=0; i++;}static void RFPrintNum(int i, int j, int k, int l, int m, int maxNum){ System.out.println(i+" "+ j+" "+ k+" "+ l+" "+m); // 종료 조건 if(i == maxNum && j == maxNum && k == maxNum && l == maxNum && m == maxNum) return; // 다음 단계로 넘어가는 조건 if (m != maxNum) {m++;} else if (l != maxNum) {m=0; l++;} else if (k != maxNum) {m=0; l=0; k++;} else if (j != maxNum) {m=0; l=0; k=0; j++;} else if (i != maxNum) {m=0; l=0; k=0; j=0; i++;} // 재귀 RFPrintNum(i,j,k,l,m,maxNum); }
◎ 재귀가 적합한 경우
-
재귀가 적합한 경우
- 주어진 문제를 비슷한 구조의 더 작은 문제로 나눌 수 있는 경우
- 중첩된 반복문이 많거나 반복문의 중첩 횟수(number of loops)를 예측하기 어려운 경우
- 변수 사용을 줄여 mutable state (변경 가능한 상태) 를 제거하여 프로그램 오류가 발생할 수 있는 가능성을 줄이는 경우
-
반복문 vs 재귀
- 모든 재귀 함수는 반복문(while 문 또는 for 문)으로 표현할 수 있다. 그러나 재귀를 적용할 수 있는 대부분의 경우에는, 재귀를 적용한 코드가 더욱 간결하고 이해하기 쉽다.
◎ 재귀함수와 메모리 사용량
-
실행컨텍스트는 메모리를 차지하기 때문에, 재귀 함수 사용시 메모리 요구사항에 유의해야한다. (재귀 함수 호출 시 마다 스택 공간을 이용하여 스택 오버플로우가 일어날 수 있음)
-
깊이(depth)를 늘리면 깊이가 줄어들 때마다 depth 만큼의 실행 컨텍스트가 저장될 메모리 공간 필요 → 반복문 기반 알고리즘을 통해 메모리 사용((=함수 호출의 비용) 절약 가능
◎ 꼬리 재귀
-
재귀 호출이 끝나면 아무 일도 하지 않고 결과만 바로 반환되도록 하는 방법
-
장점
- 이전 함수의 상태를 유지하지도 않고 추가 연산을 하지도 않아서 스택이 넘쳐나는 문제를 해결할 수 있게 된다.
- Memory Leak 방지 (필요하지 않은 메모리를 계속 점유하고 있는 현상 방지)
-
재귀 vs 꼬리 재귀
- 재귀
- 연산을 index값이 0인 부분부터 순서대로 계산
- 최종적으로 return이 될 때, 연산을 하나씩 거치면서 값이 달라짐
- 꼬리 재귀
- 연산을 index값이 큰 순서부터 계산 (재귀 함수를 호출하면서 계산)
- 최종적이로 return이 될 때, 연산없이 결과 값만을 전달함
- 호출 함수가 1개일 때 (계산 방향이 단방향일때) 만 사용 가능
// 에서는 사용 불가
// 호출시에 사용 static int sumFromZero(int n){ return sumFromZero(n, 0); } // 실제 겨산시에 사용 static int sumFromZero(int n, int acc){ if (n == 0) return acc; // n-0에 도달하면 연산 완료 return sumFromZero(n-1, acc + n); // 여러개의 call stack이 쌓였을때, 연산없이 값만을 전달해줌 } - 재귀
◎ 재귀함수 대표 예시
-
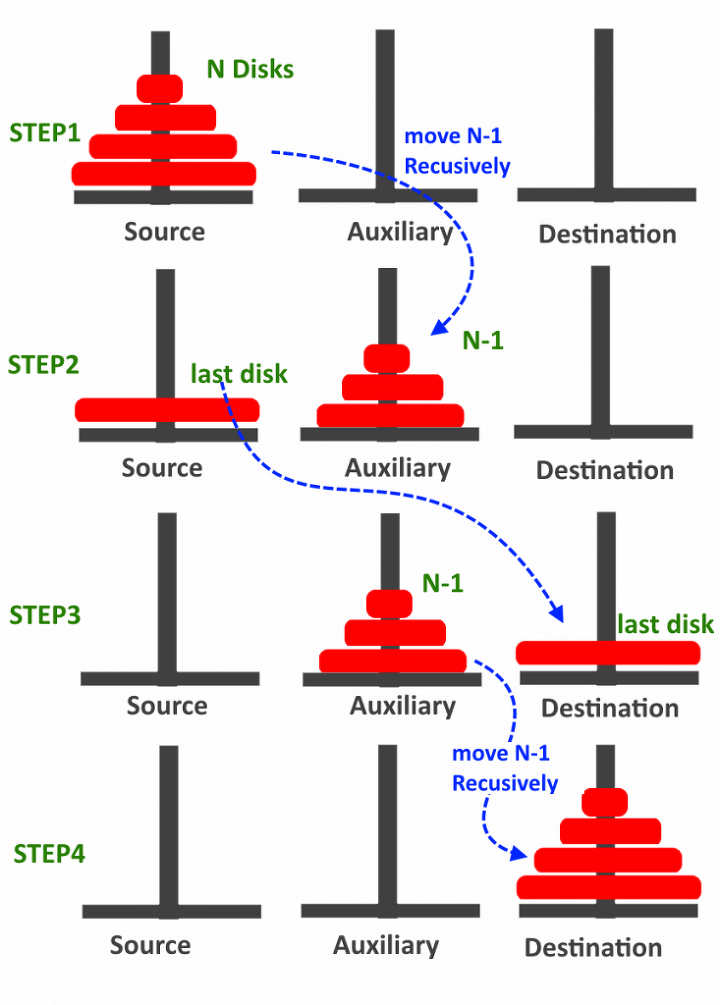
하노이의 탑 (최소 이동 횟수)
- 원리 :
- 상위 N-1개의 원반과 맨 아래 원반을 나누어 생각
- step1 상위 N-1 개의 원반을 옮김 : 번 옮김
- step2 맨 아래 원반을 목적지로 옮김 : 1번 옮김
- step3 상위 N-1 개의 원반을 맨 아래 원반 위로 옮김 : $f(N-
- 총 번 옮김 /
- 구현
// 꼬리 재귀 이용 private static long hanoi(int floor, long sum){ if(floor == 1) return sum; return hanoi(floor-1, 2*sum+1); } // 호출시 사용 static long hanoi(int floor){ return hanoi(floor, 0L); } - 원리 :
-
조합
- 정의 : 서로 다른 n개의 공 중에서 r개를 순서없이 뽑는 경우의 수
- 원리 :
- 특정 공 (1번 공) 이 있다고 하자.
- step1 1번 공을 뽑는 경우, 1번 공과 n-1중 r-1개를 뽑으면 됨 :
- step2 1번 공을 못뽑는 경우, 1번공을 제외한 n-1개 중 r개를 뽑으면 됨 :
- 모든 경우의 수는 개 이다. /
- 구현
static int combination(int n, int r){ if(r==0 || r==n) return 1; return combination(n-1,r) + combination(n-1,r-1); }
◎ 참고 블로그
- 재귀 함수 개념&예제 : https://crazykim2.tistory.com/591
- 재귀 함수 (메모리 사용량 부분 발췌) https://velog.io/@leobit/%EC%9E%AC%EA%B7%80%ED%95%A8%EC%88%98recursion
- 꼬리 재귀 최적화 : https://bozeury.tistory.com/96
- 재귀 vs 꼬리재귀 : https://joooing.tistory.com/entry/%EC%9E%AC%EA%B7%80-%E2%86%92-%EA%BC%AC%EB%A6%AC-%EC%9E%AC%EA%B7%80-Tail-Recursion