최단거리 Graph

◎ 다익스트라(Dijkstra) 알고리즘

• 조건

  • 하나의 정점에서 출발하는 최단 거리를 구함(출발지만 정함)
    - 도착 지점은 모두 구할 수 있다.
  • 음수 가중치 X

• 시간 복잡도

  • 인접 행렬로 표현된 경우: O(n^2)
  • PriorityQueue를 사용하는 경우 : O(mlogn) → 개선된 다익스트라 알고리즘

• 구현 방법

  • 필요 변수 :
    • int[] answer : 시작점은 0, 나머지는 Integer.MAX_VALUE
    • boolean[] isChecked : 모두 false
  1. 시작 노드의 가중치를 0으로 세팅 후 PriorityQueue에 넣기
  2. 아래 행동 반복 (PriorityQueue가 비어있을 때 까지)
     2-1. PriorityQueue에서 Node를 하나 꺼냄
     2-2. 한 번 방문했던 곳이라면 넘어감
     2-3. 해당 Node와 인접한 Node의 "현재 가중치 + Node 가중치"가 최솟값이면 값을 수정하고 PriorityQueue에 넣음 - 인접한 모든 Node에 수행

• 예시 : 링크 참고

◎ 벨만-포드(Bellman-Ford) 알고리즘

• 조건

  • 하나의 정점에서 출발하는 최단 거리를 구함(출발지만 정함)
  • 음수 사이클 없어야 함 (음수 가중치 허용)
    • 어떤 노드에서 자기 자신으로 돌아오는 사이클을 돌았을 때, 더한 모든 가중치가 음수가 되는 경우가 없어야 함

• 시간 복잡도 : O(mn)

• 구현 방법

  • 필요 변수
    • int[] answer : 시작점은 0, 나머지는 Integer.MAX_VALUE
    • boolean[] isChecked : 모두 false
  1. answer[] 의 값이 Integer.MAX_VALUE 값이 아닌 노드를 선택
  2. 연결된 Node의 answer[] 값을 Math.min(answer[기존], answer[현재 노드] + 가중치) 로 설정함
  3. Integer.MAX_VALUE가 아닌 노드들에 전부 반복함

• 예시 : 링크 참고

◎ 플로이드-와샬(Floyd-Warshall) 알고리즘

• 조건

  • 모든 정점에서 모든 정점까지 최단 거리를 구함
  • 음수 사이클이 없어야함 (음수 가중치는 허용)
    • 어떤 노드에서 자기 자신으로 돌아오는 사이클을 돌았을 때, 더한 모든 가중치가 음수가 되는 경우가 없어야 함
  • 그래프 비용 인접 행렬로 표현되어 있다고 가정

• 시간 복잡도 : O(n^3)

• 구현 방법

  • 필요 변수 : int[][] answer
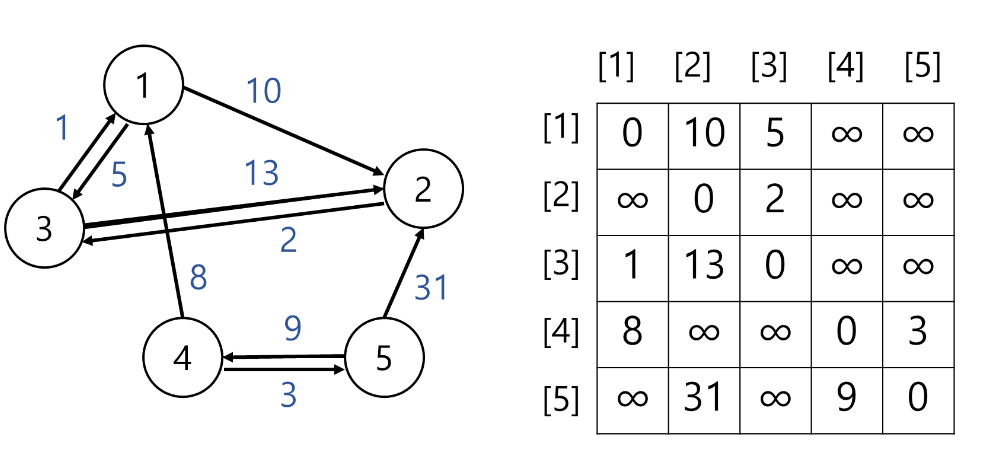
  1. 각 노드별로 한번씩 아래 단계를 진행함
  2. 1번 노드를 거쳐가는 길 중에서 더 짧은 길을 업데이트 함
     2-1. 예시 :

     answer[3][2] = Math.min(answer[3][2], answer[3][1] + answer[1][2]);
     answer[3][4] = Math.min(answer[3][4], answer[3][1] + answer[1][4]);
     ...

실제 코드 예시

• 다익스트라(Dijkstra) 알고리즘

public class Solution {

    private static final int START_NODE_INDEX = 0;

    public int[] solution(int N, int[][] road, int K) {
        int[][] matrix = makeGraphMatrix(N, road);
        int[] minimumDistance = calculateMinimumDistance(matrix, START_NODE_INDEX);
        
        return minimumDistance;
    }

    private int[][] makeGraphMatrix(int N, int[][] roads) {
        int[][] matrix = new int[N][N];

        for (int[] road : roads) {
            // 같은 길 정보 중복 시, 짧은 길을 선택하도록 함
            if (matrix[road[0]-1][road[1]-1] != 0 && matrix[road[0]-1][road[1]-1] <= road[2]) {
                continue;
            }
            matrix[road[0]-1][road[1]-1] = road[2];
            matrix[road[1]-1][road[0]-1] = road[2];
        }
        return matrix;
    }

    private int[] calculateMinimumDistance(int[][] matrix, int startIndex) {
        // answer : 정답을 가지고 있음
        int[] answer = new int[matrix.length];
        Arrays.fill(answer, Integer.MAX_VALUE);
        answer[startIndex] = 0;
		
        // isChecked : 현재 방문했는제를 확인함
        boolean[] isChecked = new boolean[matrix.length];
        PriorityQueue<Node> queue = new PriorityQueue<>();
        queue.add(new Node(startIndex, 0));

        while (!queue.isEmpty()) {
            Node currentNode = queue.remove();
            int currentIndex = currentNode.getNodeIndex();

            if (isChecked[currentNode.getNodeIndex()]) {
                continue;
            }
            isChecked[currentNode.getNodeIndex()] = true;

            for (int i=0; i < matrix.length; i++) {
                if (matrix[currentIndex][i] == 0) {
                    continue;
                }
                if (currentNode.getDistance() + matrix[currentIndex][i] < answer[i]) {
                    answer[i] = currentNode.getDistance() + matrix[currentIndex][i];
                    queue.add(new Node(i, answer[i]));
                }
            }
        }
        return answer;
    }
}

class Node implements Comparable<Node> {
    private int nodeIndex;
    private int distance;

    Node(int nodeIndex, int distance) {
        this.nodeIndex = nodeIndex;
        this.distance = distance;
    }

    public int getDistance() {
        return distance;
    }

    public int getNodeIndex() {
        return nodeIndex;
    }

    @Override
    public int compareTo(Node o) {
        return this.distance - o.distance;
    }
}